7класс геометрия. Праскова мария валериевна учитель математики мбоу гундинская сош
 Скачать 0.88 Mb.
|
|
IV. Итоги урока. Домашнее задание: изучить пункты 7, 8 из § 4; ответить на вопросы 12 и 13, с. 25; решить задачи № 24, 25, 28, 31 (a), 33, 36 (решение задачи приведено в учебнике). Урок 5. ИЗМЕРЕНИЕ УГЛОВ (§ 5) Цели: ввести понятие градусной меры угла и рассмотреть свойства градусных мер углов; ввести понятия острого, прямого и тупого углов; ознакомить учащихся с приборами для измерения углов на местности. Оборудование: демонстрационный транспортир; транспортиры у учащихся; таблица «Виды углов». I. Проверочная самостоятельная работа (10 мин) (проверка усвоения свойств длин отрезков). Вариант I 1. На прямой в отмечены точки С, Д и Е так, что СД = 6 см, ДЕ = 8 см. Какой может быть длина отрезка СЕ? (Ответ: СЕ = 14 см или СЕ = 2 см.) 2. Точка М - середина отрезка АВ; MB = 4,3 дм. Найдите длину отрезка АВ в миллиметрах. Вариант II 1. На прямой m отмечены точки А, В и С так, что АС = 12 см, АВ = 8 см. Какой может быть длина отрезка ВС? (Ответ: ВС = 20 см или ВС = 4 см.) 2. Точка Р — середина отрезка MN. Найдите длину отрезка PN в метрах, если MN = 14 дм. Вариант III (для более подготовленных учащихся) 1. Даны отрезок СД и точка М, причем СД = 17 см, СМ = 13 см, ДМ = 5 см. Лежит ли точка М на отрезке СД? 2. На прямой а отмечены последовательно точки С, Д, Е и F так, что СД = EF. Расстояние между серединами отрезков СД и EF равно 12,4 см. Найдите расстояние между точками С и Е. II. Объяснение нового материала. 1. Измерение углов аналогично измерению отрезков - оно основано на сравнении их с углом, принятым за единицу измерения. 2. Градус - угол, равный 1/180 части развернутого угла. Градусная мера угла. 3. Повторить измерение углов с помощью транспортира. (Начертить на доске и в тетрадях любые углы и измерить их с помощью транспортира; рис. 32, рис. 33.) 4. Ввести понятие минуты - это 1/60 часть градуса; запись 1', понятие секунды - это 1/60 часть минуты; записывается 1". 5. Записать в тетрадях выводы: 1) равные углы имеют равные градусные меры; 2) меньший угол имеет меньшую градусную меру; 3) развернутый угол равен 180°; неразвернутый угол меньше 180°; 4) когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов (рис. 34). 6. Выполнение практических заданий № 41, 42,43. 7. Устно решить задачи № 45, 46. 8. Ввести понятия прямого, острого и тупого углов с помощью таблицы «Виды углов» и рисунка 35. 9. Устно решить задачи № 51 (по рис. 38), № 52 (по рис. 39) и № 53. III. Закрепление изученного материала. 1 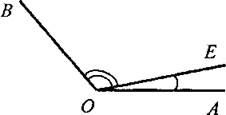 . Решить задачу № 47(6). Решение записывается на доске и в тетрадях (объясняет учитель):Дано: ∠AOE = 12°37'; ∠EOB = 108°25'. Найти: ∠AOB. Решение: ∠AOB = ∠AOE + ∠ВОЕ; ∠AOB = 12°37' + 108°25' = 120°62' = 121°2'. Ответ: 121°2'. 2. Решить задачу № 48 на доске и в тетрадях (объясняет учитель): Д 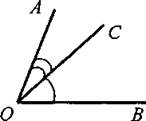 ано: ∠AOB = 78°; ∠AOC < ∠BOC на 18°.Найти: ∠BOC. Решение: По условию ∠AOB = ∠AOC + ∠BOC - 78°; ∠AOC = ∠BOC - 18°. Отсюда ∠BOC - 18° + ∠BOC = 78°; 2 · ZBOC = 78° + 18°; 2 · ZBOC = 96°, тогда ∠BOC = 96° : 2 = 48°. Ответ: 48°. 3. Решить задачу обучающего характера на доске и в тетрадях (учащиеся на доске с помощью учителя делают чертёж, записывают, что дало и что найти, учатся оформлять решение задачи): 1) Луч ВД делит развернутый угол ABC на два угла, разность которых равна 46°. Найдите образовавшиеся углы. 2) Луч СК делит прямой угол ВСМ на два угла, один из которых в 4 раза больше другого. Найти образовавшиеся углы. 3) Луч ДО делит прямой угол АДВ на два угла, градусные меры которых относятся как 5 : 4. Найдите угол между лучом ДО и биссектрисой угла АДВ. IV. Итоги урока. С помощью вопросов, задаваемых учащимся, учитель выясняет, знают ли ученики, что такое градусная мера угла, чему равны минута и секунда; умеют ли изображать прямой, острый, тупой и развернутый углы и находить градусные меры данных углов, используя транспортир. Домашнее задание: изучить пункты 9 и 10 (самостоятельно); ответить на вопросы 14-16 на с. 25-26; выполнить практическое задание № 44; решить задачи № 47(a), 49, 50. Урок 6. ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ (§ 6) Цели: ввести понятия смежных и вертикальных углов; рассмотреть их свойства; ввести понятие перпендикулярных прямых и показать, как применяются эти понятия при решении задач. Наглядные пособия: таблицы «Смежные углы», «Вертикальные углы», «Перпендикулярные прямые». I. Анализ результатов самостоятельной работы. II. Изучение нового материала. Решение задач. 1 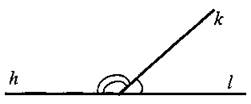 . Ввести понятие смежных углов и их свойства (сумма смежных углов равна 180°) с помощью таблицы «Смежные углы».2. Выполнение практического задания № 55 (на доске и в тетрадях). 3. Устно решить задачи № 58, 59, 60, 63, 62 (по рис. 46). 4. Письменно решить задачу № 61 (в; г): в) Дано: ∠hk и ∠kl - смежные; ∠hk больше ∠kl на 47° 18'. Найти: ∠hk и ∠kl. Решение: Пусть ∠kl = х, тогда ∠hk = х + 47°18'. По свойству о сумме смежных углов ∠kl + ∠hk = 180°. х + х + 47°18' = 180°; 2х = 180° - 47°18'; 2х - 179°60' - 47° 18'; 2х = 122°42'; х = б6°21'. ∠kl = 66°2Г; ∠hk = 66°21' + 47°18' = 113°39'. Ответ: 113°39' и 66°21'. г) Пусть ∠kl = х, тогда ∠hk = 3х х + 3х = 180°; 4х = 180°; х = 45°; ∠kl = 45°; ∠hk = 135°. Ответ: 135° и 45°. 5. Понятие вертикальных углов можно ввести, выполняя следующее задание: 1) Начертите неразвернутый ∠AOB и назовите лучи, являющиеся сторонами этого угла. 2) Проведите луч ОС, являющийся продолжением луча ОА, и луч ОД, являющийся продолжением луча ОВ. 3) Запишите в тетради: углы АОВ и СОД называются вертикальными. 6. На таблице «Вертикальные углы» показать, что при пересечении двух прямых образуются две пары вертикальных углов с вершиной в точке пересечения этих прямых. 7 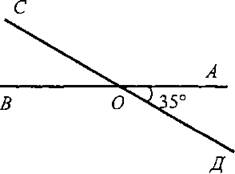 . Определение вертикальных углов (рис. 41).8. Обоснование того факта, что вертикальные углы равны, вначале можно провести на конкретном примере, записав его на доске и в тетрадях учащихся. Задача. Прямые АВ и СД пересекаются в точке О так, что ∠AOД = 35°. Найдите углы АОС и ВОС. Решение: 1) Углы АОД и АОС смежные, поэтому ∠BOC = 180° - 35° = 145°. 2) Углы АОС и ВОС также смежные, поэтому ∠BOC = 180° - 145° = 35°. Значит, ∠BOC = ∠АОД = 35°, причем эти углы являются вертикальными. Вопрос: верно ли утверждение, что любые вертикальные углы равны? 9. Самостоятельное доказательство учащимися свойства вертикальных углов (рис. 41) и запись этого доказательства в тетрадях. 10. Устно решить задачу № 65 (использовать таблицу «Вертикальные углы»). 11. Устно решить задачу № 67 по рисунку 47. 12. Ввести понятие перпендикулярных прямых (использовать таблицу «Перпендикулярные прямые» (рис. 42). 13. Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые. 14. Выполнение практического задания № 57. 15. Беседа о построении прямых углов на местности (п. 13) с демонстрацией изготовленного учащимися экера. III. Самостоятельная работа. Вариант I 1. Один из смежных углов на 27° меньше другого. Найдите оба смежных угла. 2. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 226°. Вариант II 1. Один из смежных углов в девять раз больше другого. Найдите оба смежных угла. 2. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 81° больше другого. IV. Итоги урока. Домашнее задание: изучить пункты 11-13 из § 6; ответить на вопросы 17-21 на с. 26; выполнить практическое задание № 56; решить задачи № 61 (а, б), 66 (а), 68. Повторить весь изученный материал и подготовиться к контрольной работе, просмотрев по тетрадям решение задач. Урок 7. КОНТРОЛЬНАЯ РАБОТА № 1 (1 час) Цели: проверить знания, умение решать задачи и навыки учащихся по теме «Измерение отрезков. Измерение углов. Смежные и вертикальные углы». I. Организация учащихся на выполнение работы. II. Выполнение работы по двум (трём) вариантам. Вариант I 1. Три точки В, С и Д лежат на одной прямой. Известно, что ВД = 17 см, ДС = 25 см. Какой может быть длина отрезка ВС? 2. Сумма вертикальных углов МОЕ и ДОС, образованных при пересечении прямых МС и ДЕ, равна 204°. Найдите угол МОД. 3. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла. Вариант II 1. Три точки М, N и К лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МК? 2. Сумма вертикальных углов АО В и СОД, образованных при пересечении прямых АД и ВС, равна 108°. Найдите угол ВОД. 3. С помощью транспортира начертите угол, равный 132°, и проведите биссектрису одного из смежных с ним углов. Вариант III (для более подготовленных учащихся) 1  . Лежат ли точки М, N и Р на одной прямой, если МР = 12 см, MN = 5 см, PN = 8 см?2. Найдите неразвернутые углы, образованные при пересечении двух прямых, если разность двух из них равна 37°. 3. На рисунке АВ ⊥ СД, луч ОЕ — биссектриса угла А ОД. Найдите угол СОЕ. III. Итоги урока. Домашнее задание: повторить § 1-6 и подготовиться к устному опросу, который будет проводиться во внеурочное время. Примерные варианты карточек для устного опроса учащихся. Вариант I 1. Какая точка называется серединой отрезка? 2. Отметьте точку С на прямой АВ так, чтобы точка В оказалась серединой отрезка А С. 3. Отрезок длиной 18 см разделен точкой на два неравных отрезка. Чему равно расстояние между серединами этих отрезков? Вариант II 1. Какой луч называется биссектрисой угла? 2. Начертите угол ВАС, а затем с помощью транспортира и линейки проведите луч АД так, чтобы луч АВ оказался биссектрисой угла САД. Всегда ли это выполнимо? 3. Чему равна градусная мера угла, образованного биссектрисами двух смежных углов? Вариант III 1. Какие углы называются смежными? Чему равна сумма смежных углов? Могут ли быть смежными прямой и острый углы? 2. Начертите угол, смежный с данным углом. Сколько таких углов можно начертить? 3. Градусные меры двух смежных углов относятся как 3 : 7. Найдите эти углы. Вариант IV 1. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы? Сколько пар вертикальных углов образуется при пересечении двух прямых? 2. Начертите три прямые АВ, СД и МК, пересекающиеся в точке О. Назовите пары получившихся вертикальных углов. 3. При пересечении двух прямых образовались четыре неразвернутых угла. Найдите эти углы, если сумма трех углов равна 290°. Вариант V 1. Какие прямые называются перпендикулярными? Каким свойством обладают две прямые, перпендикулярные к третьей? 2. Начертите прямую а и отметьте точку М, не лежащую на ней. С помощью чертежного угольника проведите через точку М прямую, перпендикулярную к прямой а. 3. Начертите тупой угол ABC и отметьте точку Д вне его. С помощью чертежного угольника через точку Д проведите прямые, перпендикулярные к прямым АВ и ВС. ГЛАВА 2. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ (§ 1) Во второй главе изучаются признаки равенства треугольников. Они являются основным рабочим аппаратом всего курса геометрии. Доказательства большей части теорем курса строятся по схеме: поиск равных треугольников — доказательство их равенства — следствия, вытекающие из равенства треугольников. Признаки равенства треугольников открывают широкие возможности для решения задач и, таким образом, позволяют накапливать опыт доказательных рас- суждений. Доказательства первого и второго признаков состоят в том, что один треугольник совмещается с другим путем наложения, а это означает, что треугольники равны по определению равенства фигур. Этот приём нагляден, понятен учащимся, вполне соответствует их представлениям о равенстве фигур. На начальном этапе изучения признаков равенства треугольников полезно больше внимания уделять решению задач по готовым чертежам, применяя таблицы и ТСО. В дальнейшем при решении задач данной главы нужно нацеливать учащихся на самостоятельное выполнение рисунка по условию задачи, что во многих случаях помогает быстрее найти и применить подходящий признак равенства треугольников. Второй важный момент данной главы - введение нового класса задач - на построение с помощью циркуля и линейки. Урок 1. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ (§ 1) (3 часа) Цели: ввести понятия треугольника и его элементов, периметра треугольника; учить оформлять и решать задачи; развивать логическое мышление учащихся. Оборудование: различные многоугольники и треугольники, вырезанные из бумаги или изготовленные из проволоки; таблицы «Виды треугольников» и «Равенство треугольников». I. Анализ контрольной работы. 1. Сообщение итогов контрольной работы. 2. Ошибки, допущенные учащимися в ходе работы. 3. Решение на доске задач, вызвавших затруднения у учащихся. II. Изучение нового материала методом беседы. 1. Понятие треугольника знакомо учащимся, поэтому изучение темы начинается с демонстрации различных многоугольников, треугольников, изготовленных из бумаги, проволоки либо изображенных на таблице или классной доске. 2. Учащиеся выделяют треугольники, указывают и называют их стороны, вершины и углы. Обозначение треугольника, его углов, сторон. 3. Выполнение практического задания: 1) Начертите треугольник ABC и проведите отрезок, соединяющий вершину А с серединой противоположной стороны. 2) Начертите треугольник MNP. На стороне МР отметьте произвольную точку К и соедините ее с вершиной, противолежащей стороне МР. 3) Назовите углы: а) треугольника ДЕК, прилежащие к стороне ЕК; б) треугольника MNP, прилежащие к стороне MN. 4) Назовите угол: а) треугольника ДЕК, заключенный между сторонами ДЕ и ДК; б) треугольника MNP, заключенный между сторонами NP и РМ. 5) Между какими сторонами: а) треугольника ДЕК заключен угол К, б) треугольника MNP заключен угол N? 4. Выполнение заданий № 87 и 88 для лучшего усвоения понятий треугольника и его элементов. 5. Введение понятия периметра треугольника. Записать в тетради: сумма длин трех сторон треугольника называется его периметром. 6. Решение задачи № 91 с оформлением на доске и в тетрадях учащихся: Дано: РΔАВС = 48 см, АС = 18 см, ВС - АВ = 4,6 см. Найти: АВ и ВС. Решение: Обозначим длину стороны АВ в сантиметрах буквой х, тогда ВС = (х + 4,6) см; 48 см = АВ + АС + ВС = х + х + 4,6 + 18 см, откуда 2х - 25,4; х = 12,7. Значит, АВ = 12,7 см; ВС = 12,7 + 4,6 + 17,3 (см). Ответ: 12,7 см и 17,3 см. 7. Вспомнить, какие фигуры называются равными. Записать в тетрадях определение: Два треугольника называются равными, если каждой стороне и каждому углу в любом из них найдется равный элемент в другом. 8. Работа по рис. 50 и таблице «Равенство треугольников». О  братить внимание учащихся на то, что из равенства треугольников следует равенство соответствующих, то есть совмещающихся при наложении сторон и углов этих треугольников, и что в равных треугольниках против соответственно равных сторон лежат равные углы и обратно, против соответственно равных углов лежат равные стороны.9. Устно решить задание: на каждом из рисунков 1 и 2 изображены равные между собой треугольники. Указать соответственно равные элементы этих треугольников. 10. Устное решение задачи № 92. 11. Письменно решить задачу: Треугольники ABC и MNP равны, причем ∠A = ∠M, ∠B = ∠N и ∠C = ∠P. Найдите стороны ΔМNР, если АВ = 7 см, ВС = 5 см, СА = 3 см. Решение: ΔABC = ΔМNP по условию, поэтому углы и стороны ΔABC соответственно равны углам и сторонам треугольника MNP. Из условия задачи следует, что соответственно равными являются стороны АВ и MN, ВС и NP, СА и РМ. Значит, MN = 7 см, NP = 5 см, РМ = 3 см. |