7класс геометрия. Праскова мария валериевна учитель математики мбоу гундинская сош
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
Урок 2.ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ 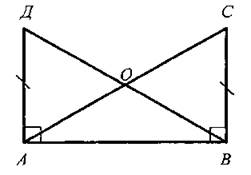 Цели: доказать признаки равенства прямоугольных треугольников и показать, как они применяются при решении задач. Цели: доказать признаки равенства прямоугольных треугольников и показать, как они применяются при решении задач.I. Повторение изученного материала. 1. Сформулировать свойства прямоугольных треугольников. 2. Вспомнить признаки равенства треугольников. 3. Решить задачу: гипотенузы ВД и АС прямоугольных треугольников АВД и ABC с общим катетом АВ и с равными катетами АД и ВС пересекаются в точке О (см. рис.). Докажите, что треугольник АОВ равнобедренный. II. Изучение нового материала. 1. Учащиеся самостоятельно (устно), используя признаки равенства треугольников, доказывают признаки равенства прямоугольных треугольников по двум катетам, по катету и прилежащему острому углу, по гипотенузе и острому углу (учитель держит перед классом два равных прямоугольных треугольника и задает наводящие вопросы). 2. Доказательство признака равенства прямоугольных треугольников по гипотенузе и острому углу (устно) по моделям равных прямоугольных треугольников. 3. Доказательство признака равенства прямоугольных треугольников по гипотенузе и катету проводит сам учитель (рис. 133 учебника), так как доказательство этого признака требует дополнительных построений и непростых логических рассуждений. I 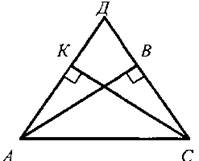 II. Закрепление изученного материала. II. Закрепление изученного материала.1. Решить задачу № 261 на доске и в тетрадях. Дано: ΔАДС; АД = ДС; АВ и СК - высоты. Доказать: АВ = СК. Доказательство: По условию АВ ⊥ ДС и СК ⊥ АД, тогда ΔАВС и ΔАКС - прямоугольные; в них АС - общая гипотенуза и ∠KAC = ∠ВСА, так как по условию ΔАДС равнобедренный. Значит, ΔАВС = ΔСКА (по гипотенузе и острому углу). Тогда АВ = СК. 2. Учащиеся самостоятельно формулируют и доказывают признак равенства прямоугольных треугольников по катету и противолежащему углу (задача № 268). 3. Решить задачу № 269 на доске и в тетрадях. Указание: при решении задачи применить вывод задачи № 268 - признак равенства прямоугольных треугольников по катету и противолежащему углу. IV. Итоги урока. Домашнее задание: изучить п. 35; ответить на вопросы 12-13 на с. 90; решить задачи № 262, 264. Урок 3. РЕШЕНИЕ ЗАДАЧ Цели: научить применять признаки равенства прямоугольных треугольников и их свойства при решении задач; вырабатывать умение решать задачи; учить логически мыслить. I. Устная работа. 1. Сформулировать свойства прямоугольных треугольников. 2. Сформулировать признаки равенства прямоугольных треугольников. 3. Устно решить задачи по готовым чертежам: 1) На рисунке 1 ∠5 = ∠C = 90°; ∠1 = ∠2. Докажите, что АВ = СД. 2) На рисунке 2 АВ = СД; ВС = АД, ∠AFB = ∠СЕД = 90°. Докажите, что BF = ЕД; AF = ЕС. 3) На рисунке 3 ∠1 = ∠2 = 90°, АВ = ДС. Докажите, что ВС = АД. 4) На рисунке 4 АН и А1Н1 - высоты треугольников ABC и А1В1С1; АС = А1С1; ∠1 = ∠2; AH = A1H1. Докажите, что ΔАВС = ΔА1В1С1. 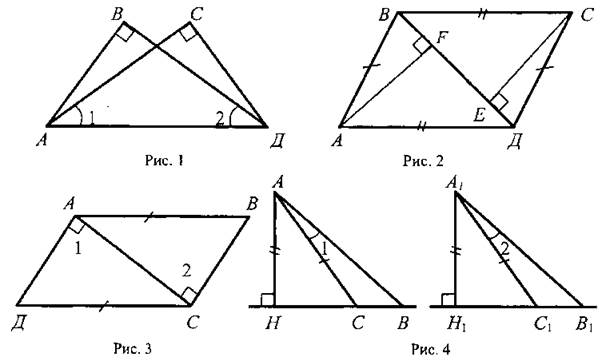 II. Решение задач. 1. Решить задачу № 263 на доске и в тетрадях. 2. Решить задачу № 267 на доске и в тетрадях. Указание: при доказательстве применить признак равенства прямоугольных треугольников по гипотенузе и катету. III. Самостоятельная работа (проверочного характера) (20 мин). Вариант I 1. На рисунке 5 АД = ДС; ЕД = ДF; ∠1 = ∠2 = 90°. Докажите, что треугольник ABC равнобедренный. 2. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет. Вариант II 1. На рисунке 6 ∠1 = ∠2, ∠3 = ∠4 = 90°; ВД = ДС. Докажите, что треугольник ABC равнобедренный. 2. Один из острых углов прямоугольного треугольника в два раза меньше другого, а разность гипотенузы и меньшего катета равна 15 см. Найдите гипотенузу и меньший катет. Вариант III (для более подготовленных учащихся) 1. Через середину отрезка АВ проведена прямая а. Из точек А и В к прямой а проведены перпендикуляры АС и ВД. Докажите, что АС = ВД. 2. В прямоугольном треугольнике СДЕ с прямым углом Е проведена высота EF. Найдите CF и РД, если СД = 18 см, а ∠ДСЕ = 30°. Вариант IV (для более подготовленных учащихся) 1. Из точки М биссектрисы неразвернутого угла О проведены перпендикуляры МА и MB к сторонам этого угла. Докажите, что МА = MB. 2. В прямоугольном треугольнике ABC с гипотенузой АВ и ∠A = 60° проведена высота СН. Найдите ВН, если АН = 6 см. 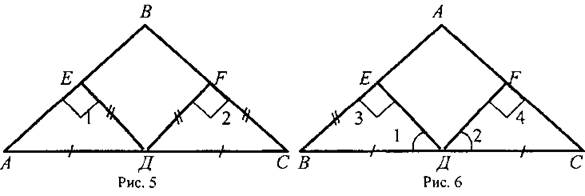 IV. Итоги урока. Домашнее задание: повторить пункты 30-35; подготовиться к устному опросу по карточкам; прочитать п. 36; решить № 258, 265. Урок 4. РЕШЕНИЕ ЗАДАЧ Цели: повторить и систематизировать ранее изученный материал; вырабатывать навыки в решении задач; развивать логическое мышление учащихся. I. Анализ результатов самостоятельной работы. 1. Указать ошибки учащихся в решении задач. 2. Решить задачи, вызвавшие затруднения у учащихся. II. Устный опрос учащихся по карточкам. Вариант I 1. Сформулируйте теорему о сумме углов треугольника. 2. Один из углов при основании равнобедренного треугольника равен 65°. Найдите остальные углы треугольника. 3. В треугольнике ABC ∠B = 110°; биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС. Вариант II 1. Сформулируйте свойство катета прямоугольного треугольника, лежащего против угла в 30°. 2. В прямоугольном треугольнике ABC ∠C = 90°; ∠B = 60°, АВ = 15 см. Найдите ВС. 3. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу. Вариант III 1. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету. 2. В треугольниках ABC и А1В1С1 ∠B = ∠B1 = 90°; АВ = A1B1, AC = А1С1. Найдите углы А1 и С1 треугольника А1В1С1, если ∠A = 34°; ∠C = 54°. 3. На сторонах угла Л отмечены точки В и С так, что AB = AС. Через точки В и С проведены прямые, перпендикулярные соответственно к сторонам АВ и АС данного угла и пересекающиеся в точке М. Докажите, что MB = МС. Вариант IV 1. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и острому углу. 2. В треугольниках ABC и А1В1С1 углы В и В1 прямые, ∠A = ∠A1, AC = А1С1. Найдите стороны В1С1, и А1В1 треугольника А1В1С1, если ВС = 17 см, АВ = 12 см. 3. Даны два равных прямоугольных треугольника ABC и А1В1С1, у которых ∠B = ∠B1 = 90°, ∠A = ∠A1; ВН и В1Н1 - высоты. Докажите, что ΔВНС = ΔВ1Н1С1. I 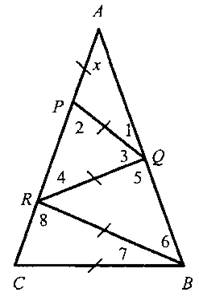 II. Решение задач. II. Решение задач.1. Решить задачу № 299 на доске и в тетрадях. Решение: При решении удобно обозначить ∠A = х и ввести обозначения цифровые для углов, как показано на рисунке. 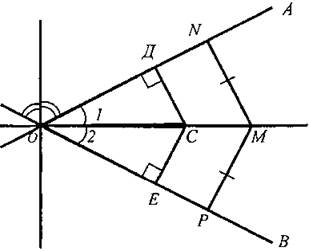 Итак, ∠A = х, поэтому ∠1 = ∠A = х, ∠2 = 2х (как внешний угол ΔAPQ), ∠4 = ∠2 = 2х; ∠3 = 180° - (v2 + ∠4) = 180° - 4х; ∠5 = 180° - (∠1 + ∠3) = 3х; ∠6 = ∠5 = 3х. Далее, ∠7 = ∠B - ∠6, но Итак, ∠A = х, поэтому ∠1 = ∠A = х, ∠2 = 2х (как внешний угол ΔAPQ), ∠4 = ∠2 = 2х; ∠3 = 180° - (v2 + ∠4) = 180° - 4х; ∠5 = 180° - (∠1 + ∠3) = 3х; ∠6 = ∠5 = 3х. Далее, ∠7 = ∠B - ∠6, но 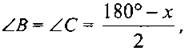 поэтому поэтому 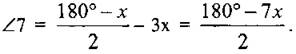 Так как ∠8 = ∠C, то ∠C + ∠8 + ∠7 = 2∠C + Z7 = 180°, или Так как ∠8 = ∠C, то ∠C + ∠8 + ∠7 = 2∠C + Z7 = 180°, или 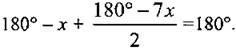 Отсюда получаем, что х = 20°. Значит,∠A = 20°. Отсюда получаем, что х = 20°. Значит,∠A = 20°.Ответ: 20°. 2. Решить задачу № 311 на доске и в тетрадях. Решение Проведем биссектрисы углов, образованных при пересечении двух прямых, ОА и ОВ. Возьмем произвольную точку С на одной из биссектрис и докажем, что она равноудалена от прямых ОА и ОВ, то есть докажем, что СД = СЕ. В самом деле, прямоугольные треугольники ОДС и ОЕС равны по гипотенузе (ОС — общая гипотенуза) и острому углу (∠1 = ∠2), поэтому СД = СЕ. Докажем теперь, что любая точка М, расположенная внутри угла АОВ и равноудаленная от сторон ОА и ОВ, лежит на биссектрисе этого угла. Для этого проведем перпендикуляры MN и МР к прямым ОА и ОВ и рассмотрим прямоугольные треугольники ONM и ОРМ. Они равны по катету и гипотенузе (ОМ - общая гипотенуза, MN = МР, так как по условию точка М равноудалена от сторон ОА и ОВ), поэтому ∠NOM = ∠POM, то есть луч ОМ - биссектриса угла АОВ. Из доказанных утверждений следует, что искомое множество точек состоит из двух прямых, содержащих биссектрисы углов, образованных при пересечении данных прямых. IV. Итоги урока. Домашнее задание: повторить пункты 15-33; решить задачи № 266,297; принести циркули и линейки. ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА ПО ТРЕМ ЭЛЕМЕНТАМ (§ 4) Урок 1. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ. РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ Цели: ввести понятия расстояния от точки до прямой и расстояния между параллельными прямыми, показать, как они применяются при решении задач. I. Изучение нового материала. 1. Ввести понятия расстояния от точки до прямой (рис. 136): 1) понятие наклонной - отрезок AM; 2) перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой; 3) длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой. 2. Рассмотреть рисунок 137. 3. Рассмотреть одно из важнейших свойств параллельных прямых: разобрать доказательство теоремы «Все точки каждой из двух параллельных прямых равноудалены от другой прямой» по рисунку 138. 4. Ввести понятие расстояния между параллельными прямыми: расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми. 5. Справедливо утверждение, обратное доказанной теореме. Оно лежит в основе конструкции рейсмуса (рис. 139 учебника), применяемого в столярном деле для разметки прямых, параллельных краю бруска (рис. 139). II. Закрепление изученного материала. 1. Решить задачи № 271, 275 на доске и в тетрадях. 2. Решить задачу № 278. Указание: воспользоваться свойством катета, лежащего в прямоугольном треугольнике против угла в 30°. 3. Устно решить задачи № 281, 282 по готовым чертежам. III. Итоги урока. Домашнее задание: изучить п. 37; ответить на вопросы 14-18 на с. 90 учебника; решить задачи № 272, 277, 283; принести циркули и линейки. Урок 2. ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА ПО ТРЕМ ЭЛЕМЕНТАМ Цель: рассмотреть задачи на построение треугольника по трем элементам. I. Проверка домашнего задания. 1. Фронтальный опрос учащихся по изученному ранее материалу. 2. Ответить на вопросы 14-18 на с. 90. 3. Двое учащихся на доске решают домашние задачи № 272, 277. II. Объяснение нового материала. 1. Напомнить учащимся, что значит решить задачу на построение с помощью циркуля и линейки; можно рассказать о том, что обычно задачи на построение решаются по схеме, состоящей из четырех частей: 1) анализ; 2) построение; 3) доказательство; 4) исследование (описание схемы содержится в пункте «Задачи повышенной трудности к главам III и IV» на с. 92-94 учебника). Вместе с тем нужно иметь в виду, что в VII классе, как правило, следует ограничиться только выполнением и описанием построения. В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи. 2. Рассмотреть решение задачи № 1. Построить треугольник по двум сторонам и углу между ними (рис. 140). 3. Разобрать решение задачи № 2. Построить треугольник по стороне и двум прилежащим к ней углам. 4. Решить задачу № 284 (рис. 142). (Решение приведено в учебнике на с. 87.) 5. Решить задачу № 290 (а) на доске и в тетрадях. III. Итоги урока. Домашнее задание: изучить п. 38 (1 и 2); решить задачи № 274, 285. Уроки 3 и 4. ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА ПО ТРЕМ ЭЛЕМЕНТАМ. ЗАДАЧИ НА ПОСТРОЕНИЕ Цель: научить учащихся решать задачи на построение, используя циркуль и линейку. I. Ответы на вопросы учащихся по домашнему заданию. II. Изучение нового материала. 1. Разобрать решение задачи № 3 на доске и в тетрадях. Построить треугольник по трем сторонам (рис. 141 и решение задачи на с. 85-86 учебника). Провести исследование, всегда ли задача № 3 имеет решение. 2. Решить задачи № 286, 289, 290 (б), 291 (в), 292, 293 на доске и в тетрадях. Решение задачи № 293 приведено в учебнике на с. 88-89. III. Самостоятельная работа (проверочного характера) (20-25 мин). Вариант I 1. Постройте прямоугольный треугольник по катету и прилежащему острому углу. 2. Даны отрезки PQ и P1Q1 и угол hk. Постройте треугольник СДЕ так, чтобы СЕ = PQ, ∠C = ∠hk, CF = P1Q1, где CF - высота треугольника. Вариант II 1. Постройте равнобедренный треугольник по основанию и медиане, проведенной к основанию. 2. Даны отрезки PQ и P1Q1 и P2Q2. Постройте треугольник EKF так, чтобы EF = PQ, KF = P1Q1 и FД = P2Q2, где FД - высота треугольника. IV. Итоги урока. Домашнее задание: пункты 37-38; вопросы 14—20 на с. 90; решить задачи № 273, 287, 288, 291 (а, б, г). Наиболее подготовленным учащимся можно предложить задачи № 294, 295, 303, 304. Урок 5. РЕШЕНИЕ ЗАДАЧ (1 час) Цели: закрепить в процессе решения задач усвоение изученного материала по теме «Прямоугольные треугольники», продолжить формирование навыков в решении задач на построение. I. Анализ результатов самостоятельной работы. II. Решение задач. 1. На доске и в тетрадях решить задачи № 301, 302, 308, 310, 314 (б, в), 315 (а, ж, з), 318. 2  . Построить прямоугольный треугольник по гипотенузе и внешнему углу при вершине острого угла. . Построить прямоугольный треугольник по гипотенузе и внешнему углу при вершине острого угла.Решение: Начертим данные отрезок PQ и угол hk. Построение: 1) Проведем прямую, отметим на ней точку В и отложим отрезок ВС, равный PQ. 2) Отложим от луча ВД, являющегося продолжением луча ВС, угол ДВМ, равный углу hk. 3 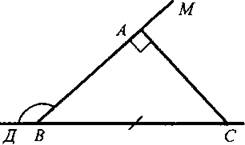 ) Построим прямую, проходящую через точку С и перпендикулярную к прямой ВМ, и обозначим буквой А точку пересечения этой прямой с лучом ВМ. Треугольник ABC искомый. ) Построим прямую, проходящую через точку С и перпендикулярную к прямой ВМ, и обозначим буквой А точку пересечения этой прямой с лучом ВМ. Треугольник ABC искомый.Доказательство (устно): По построению треугольник ABC - прямоугольный, гипотенуза ВС равна данному отрезку PQ и внешний угол АВД треугольника равен данному углу hk. Таким образом, построенный треугольник ABC удовлетворяет всем условиям задачи. Указание: задача имеет решение только в том случае, когда данный угол hk тупой. Желательно, чтобы учащиеся сами обосновали справедливость этого утверждения. III. Итоги урока. Домашнее задание: подготовиться к контрольной работе, повторить пункты 34-38; решить задачи № 307, 314 (а), 315 (а). Урок 6. КОНТРОЛЬНАЯ РАБОТА № 5 (1 час) Цели: проверить знания учащихся и их умение решать задачи; выяснить пробелы в знаниях учащихся с тем, чтобы их ликвидировать на уроках повторения. I. Организация учащихся на выполнение работы по двум вариантам. II. Выполнение учащимися работы. Вариант I 1. В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОК = 9 см. Найдите расстояние от точки О до прямой MN. 2. Постройте прямоугольный треугольник по гипотенузе и острому углу. Дополнительное задание. С помощью циркуля и линейки постройте угол, равный 150°. Вариант II 1. В прямоугольном треугольнике ДСЕ с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F до прямой ДЕ. 2. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу. Дополнительное задание. С помощью циркуля и линейки постройте угол, равный 105°. III. Итоги урока. Домашнее задание: повторить пункты 1-14 на с. 5-29 учебника. ПОВТОРЕНИЕ. РЕШЕНИЕ ЗАДАЧ (4 часа) На четырех уроках, которые отводятся на решение задач и повторение всего учебного материала курса геометрии VII класса, полезно сконцентрировать внимание учащихся на следующих узловых вопросах курса: 1. Измерение отрезков и углов; перпендикулярные прямые (1 час). 2. Треугольники: признаки равенства треугольников; равнобедренные треугольники, сумма углов треугольника, соотношения между сторонами и углами треугольника, прямоугольные треугольники (2 часа). 3. Параллельные прямые. Решение задач (1 час). На уроках повторения следует систематизировать сведения об основных свойствах геометрических фигур, повторить доказательства отдельных наиболее важных теорем. При этом могут быть использованы заранее подготовленные карточки для устного опроса, составленные по материалу каждой главы. Целесообразно не менее половины каждого урока отводить на решение задач. Рекомендуется использовать следующие задачи учебника: 33, 36, 61, 65, 70, 82, 83, 156, 162, 170, 172, 193, 204, 208, 244, 259, 269, 286, 291, 294. Отдельным ученикам, которые проявляют особый интерес к изучению геометрии, можно предложить некоторые из задач повышенной трудности (задачи № 322-362). |
