СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ ГЛАВНОГО ДВИГАТЕЛЯ. Курсовая раб. по автом-ке. Правила эксплуатации и технического обслуживания. Технические требования к регуляторам частоты вращения. Расчет динамических характеристик судового двигателя

• Название: Правила эксплуатации и технического обслуживания. Технические требования к регуляторам частоты вращения. Расчет динамических характеристик судового двигателя
• Анкор: СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ ГЛАВНОГО ДВИГАТЕЛЯ
• Дата: 19.11.2021
• Размер: 1 Mb.
• Имя файла: Курсовая раб. по автом-ке.doc
• Тип: Правила; #276564
• страница: 4 из 4

Уравнение гибкой обратной связи (изодрома).

Рис.1 Изодром.

Необходимо получить зависимость: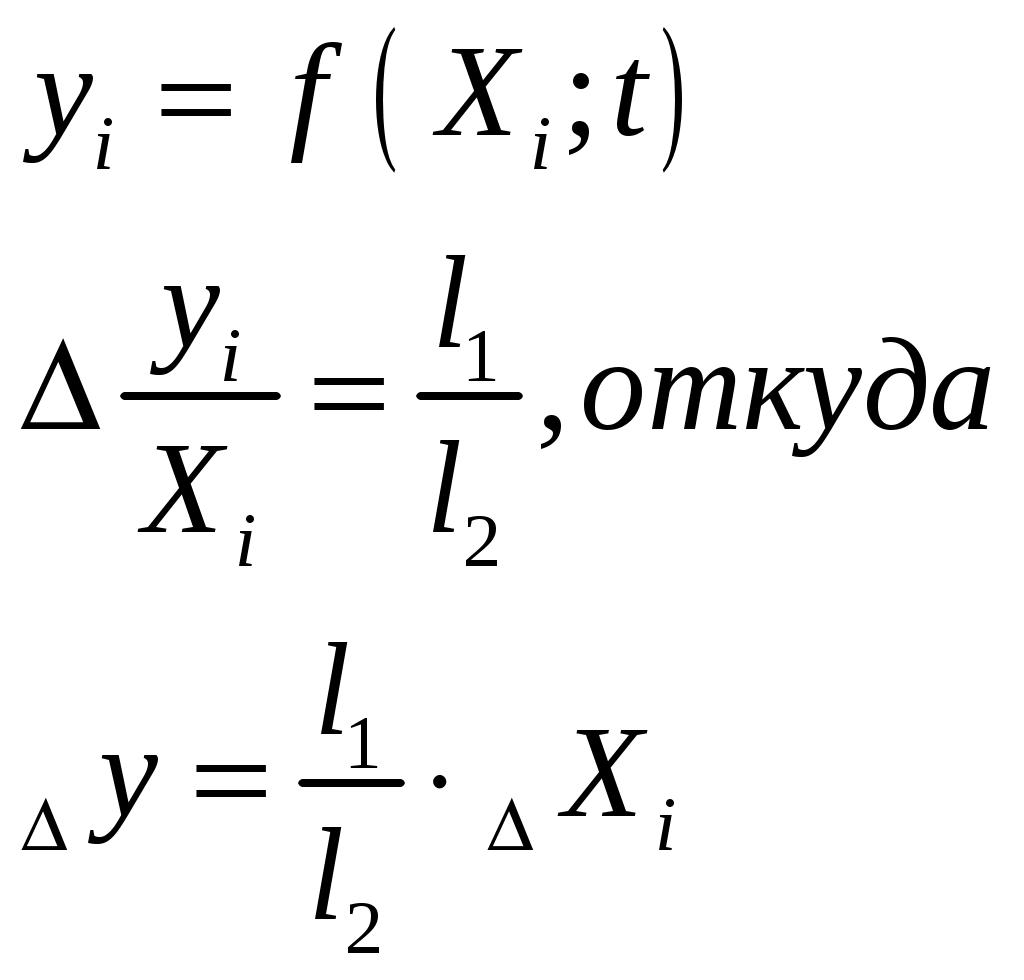



где - относительное перемещение дающего поршня;

- относительное изменение входного сигнала;

- коэффициент усиления ГОС;



Гидравлическая часть изодрома;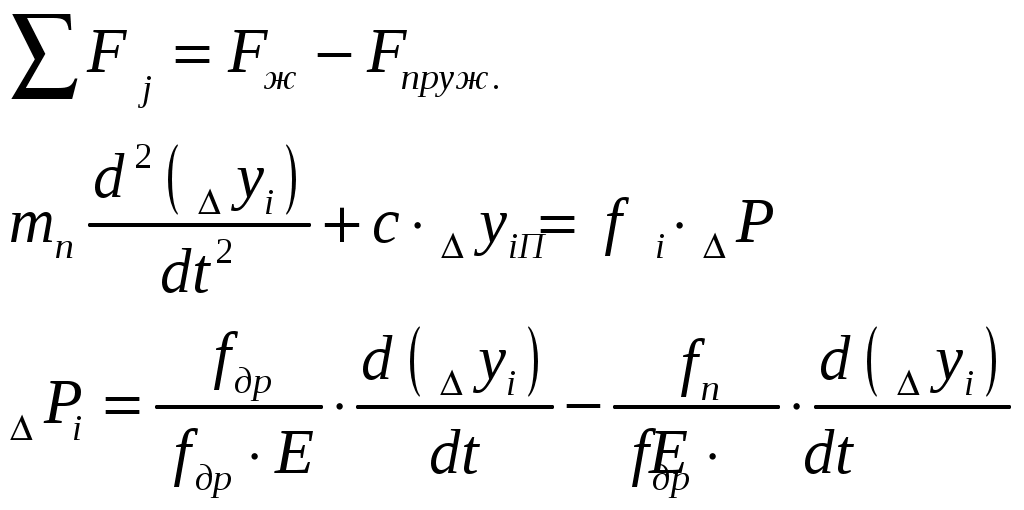
- сила инерции – результирующая всех сил;

- сила инерции приемного поршня;

- сила противодействующая пружины;

.

Подставим, приведем к безразмерной форме, приведем подобные:



где - постоянная времени изодрома, учитывающая массу поршня;

- постоянная времени изодрома, показывает за сколько времени исчезает неравномерность;

-относительное изменение выходного сигнала;

- соотношение объемов дающего и приемного поршня;

- координаты усиления ЖОС (настраиваемая величина, зависящая от соотношения плеч рычага обратной связи – положение точки опоры ).

Учитывая, что масса приемного поршня не велика, то первое слагаемое уберем, тогда:

.
Динамика жесткой обратной связи.

Рис.4 Жесткая обратная связь.

Это уравнение, определяющее зависимость входным и выходным коэффициентами, получим как уравнения движения кинематического звена. Связь охватывает два звена: усилитель и измеритель и является силовой.

Уравнение, связывающее приращения входной и выходной координат, запишется так:

.

где а – эксцентриситет, который настраивается путем изменение общей длины рычага (а + в).

И в относительных координатах: ,

Где - коэффициент обратной связи, равный .
Динамика регулятора.
Динамика регулятора в целом будет описываться получившимися уравнениями движения его элементов и уравнения связи между координатами.

Уравнение измерителя:

.

Уравнение усилителя:

.

Уравнение КГОС:

.

Уравнение ЖОС:

.

Уравнение связи между координатами:

.

Справедливо при условии, что номинальные значения координат выбраны с учетом соотношений:





Выходная координата регулятора , ввиду его воздействия на сторону подвода объекта, имеет знак, обратный знаку координаты усилителя , поэтому .

Уравнение движения дифференциального рычага BQ описывает связь между выходной координатой измерителя (или ), входной координатой усилителя (или ) и выходной координатой КГОС :



Переходя к относительным величинам, получаем что справедливо, если



С учетом уравнений связей динамика регулятора непрямого действия, входными координатами которого являются и , а выходной , описываются шестью уравнениями.

Если исключить промежуточные координаты , выр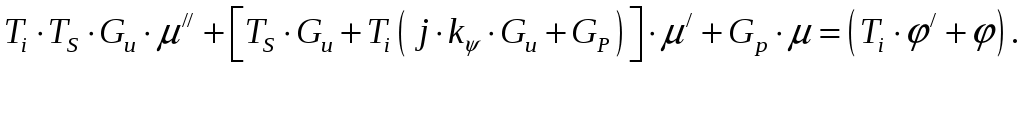азить через и , а затем подставить значения и в уравнение изодромной обратной связи, то получим следующее упрощенное уравнение динамики регулятора непрямого действия:



или



где


Это является следствием того, что жесткой обратной связью охвачены два элемента:

усилитель и измеритель. Остаточная неравномерность такого регулятора определяется коэффициентом обратной связи , что видно из выражения: . Если =0, то и =0, т.е. регулятор будет обладать астатической характеристикой на установившихся режимах.

Оптимизация переходного процесса .
Уравнение регулятора “ПИ+П” выводится следующим образом:
Движение регулятора непрямого действия при неизвестной координате задания ( ) может быть описано системой следующих уравнений.
-уравнение измерителя;

- уравнение усилителя;

- уравнение изодромной обратной связи;

- уравнение жесткой обратной связи;

- связь между координатами;

- Уравнение дифференциального рычага;

- связь выходных координат усилителя и регулятора.

Необходимо получить зависимость выходной координаты регулятора от входной и от координаты задания - во времени.

1. 
   Подставим 4 с учетом 5 и 7.
   

( )

2. 
   Подставим 6 с учетом равенства 7.
   

( )

3. 
   Подставим 5 с учетом равенства 7.
   

( )


( ) ( )

( )
( )

Из ( ) выражаем и подставляем в ( ), получим:




Отсюда


Эти выражения подставим в ( ), получим:



Или:

Если все уравнения разделить на 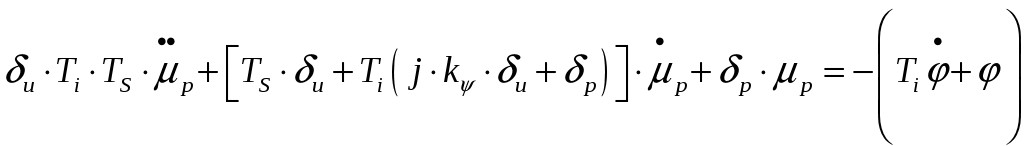и принять обозначения:
-степень неравномерности усилителя;
- степень неравномерности регулятора, получим:


Преобразование дифференциальных уравнений двигателя и регулятора в машинный вариант для просчета в программе “difr 02. bas”.

Схема дифференциальных уравнений: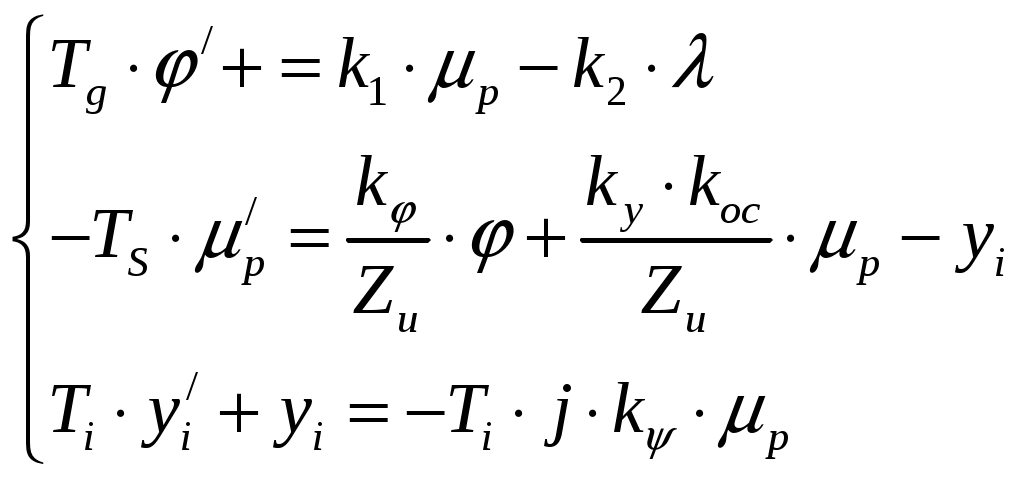




Примем обозначения: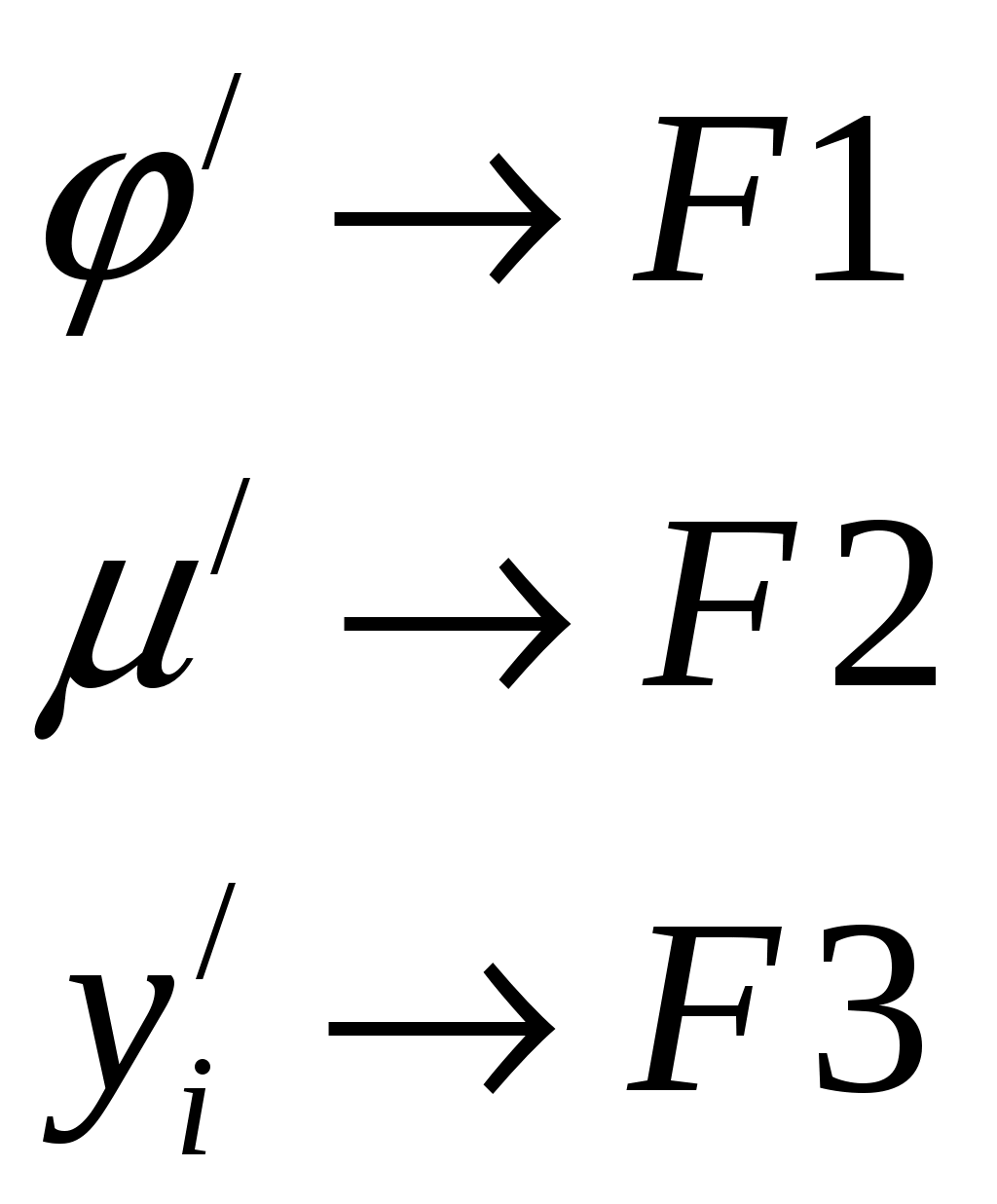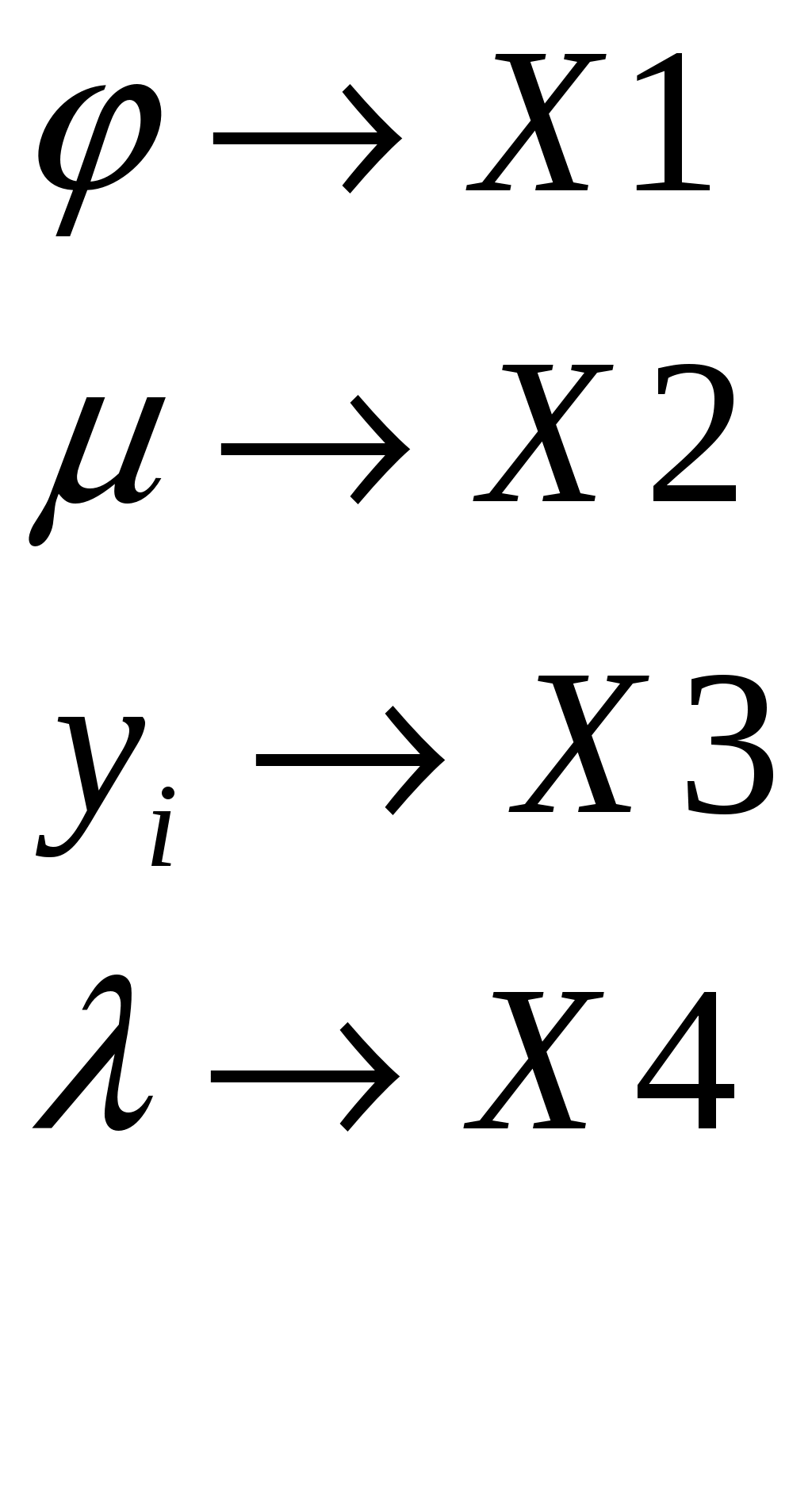



Тогда: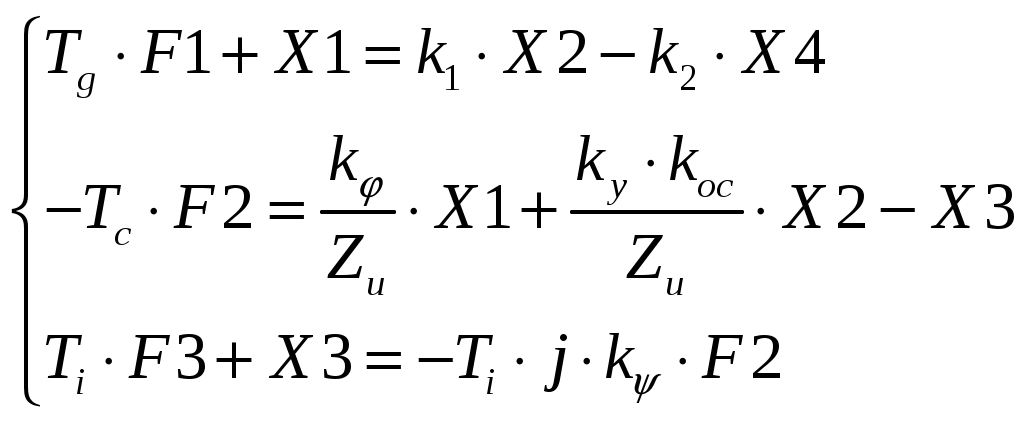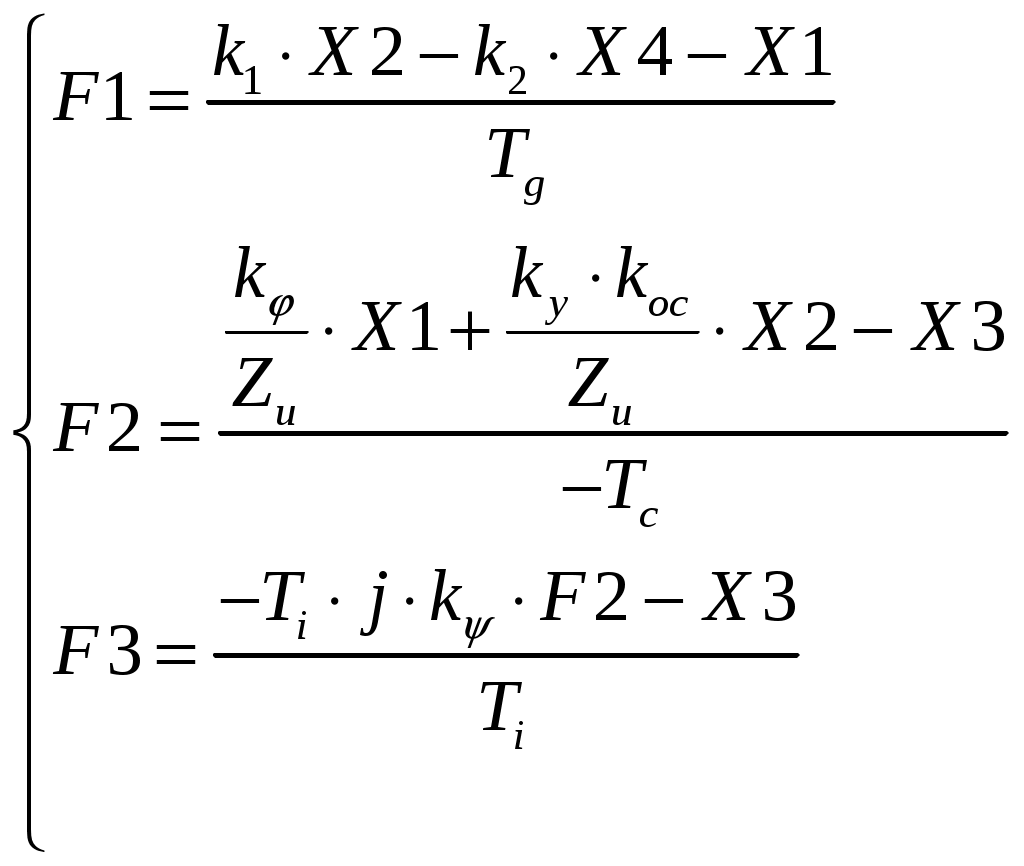




Учитывая исходные данные и расчеты, произведенные в п.5 запишем: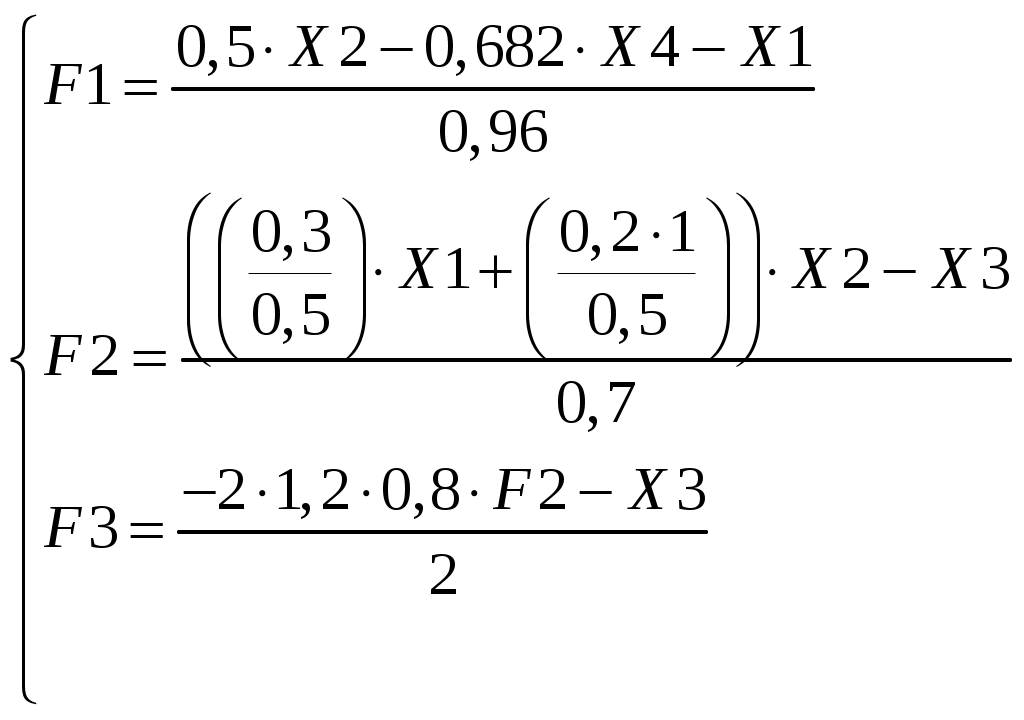


В этом виде заносим уравнения в программу “difr 02. bas”.
По результатам расчетов уравнений программой “difr 02. bas.” Можно сделать вывод о том, параметры переходного процесса выходят за пределы допустимого, следовательно необходима настройка регулятора ,т.е. изменение его настроечных параметров.

Во время настройки, для получения качественного переходного процесса, отвечающего требованиям, были изменены следующие параметры до следующих величин:

1) =0,1

2) =2

3) =0,034

4) =0,25

5) =0,03

Конечное дифференциальное уравнение:
F1=(.5*X2-.6*X4-X1)/.98

F2=-((.3/.5)*X1+((.2*.03)/.5)*X2-X3)/.034

F3=(-2*.25*.1*F2-X3)/2

ОКОНЧАНИЕ РАСЧЕТА ПО ЗАДАННОМУ ПРЕДЕЛЬНОМУ ВРЕМЕНИ СЧЕТА
0.100 6.122 0.001 0.001-100.000

1.000 8.995-172.564 3.481-100.000

2.000 2.465 -80.203 0.232-100.000

3.100 3.223-131.764 1.104-100.000

4.100 3.148-105.184 0.162-100.000

5.100 2.598-120.062 0.375-100.000

6.100 2.646-112.359 0.082-100.000

7.100 2.407-116.703 0.129-100.000

8.100 2.438-114.487 0.037-100.000

9.100 2.344-115.750 0.045-100.000

10.000 2.345-115.087 0.016-100.000

11.000 2.329-115.500 0.017-100.000

12.000 2.323-115.294 0.006-100.000

13.000 2.315-115.416 0.006-100.000

14.000 2.314-115.357 0.003-100.000

15.000 2.310-115.393 0.002-100.000

Оценка влияния параметров настройки на процесс регулирования будем производить по четырем основным критериям.

1. 
   Динамический заброс .
   
2. 
   Степень колебательности (перерегулирования) .
   
3. 
   Время регулирования .
   
4. 
   Остаточная неравномерность.
   

1. 
   Влияния - коэффициента усиления ЖОС.
   

Вывод:

1. 
   С увеличением возрастает динамический заброс .
   
2. 
   С увеличением возрастает остаточная неравномерность .
   
3. 
   - время регулирования при увеличении до оптимального значения уменьшается, при дальнейшем увеличении - увеличивается.
   

2. 
   Влияние - времени сервомотора.
   

Вывод:

При уменьшении уменьшается динамический заброс, степень неравномерности, степень колебательности и время регулирования.

Но нельзя забывать, что конструктивно практически невозможно получить очень маленькие и то, что нельзя уменьшать до бесконечности т.к. при его уменьшении меньшее критическая система теряет устойчивость.

3. 
   Влияние изменения - коэффициента усиления ИОС.
   

Вывод:
Постоянство при изменении объясняется тем, что он действует только в начале процесса регулирования, а потом его действие исчезает вместе с действием ИОС. При увеличении увеличивается динамический заброс, но при этом уменьшается степень колебательности.

- время регулирования ведет себя таким образом. При уменьшении до какого – то оптимального значения уменьшается , увеличивается.

4.Влияние изменения - времени изодрома на процесс регулирования.

Вывод:

При увеличении увеличивается динамический заброс и незначительно возрастает остаточная неравномерность. При уменьшении увеличивается степень колебательности.

- время регулирования при увеличении сначала постепенно снижается, затем практически не меняется после .


8. Список литературы.
1. Е. Г. Курзенков. “ Получение уравнения динамики и динамических характеристик главного двигателя” – Владивосток. 1984г.

2. М. И. Исаков, Л. И. Кутьин “ Комплексная автоматизация судовых дизельных и газотурбинных установок” – Ленинград, 1984г.

3. В. И. Лангуновский, А. В. Козьмирных “ Автоматизированные системы управления СДУ и ГТУ” – Т – М., 1983г.

4. В. Ф. Сыромятников “Основы автоматики и комплексная автоматизация судовых пароэнергетических установок”. – Транспор. М., 1983г.

<>