СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ ГЛАВНОГО ДВИГАТЕЛЯ. Курсовая раб. по автом-ке. Правила эксплуатации и технического обслуживания. Технические требования к регуляторам частоты вращения. Расчет динамических характеристик судового двигателя
 Скачать 1 Mb.
|
|
Значения частной производной. Табл.№6
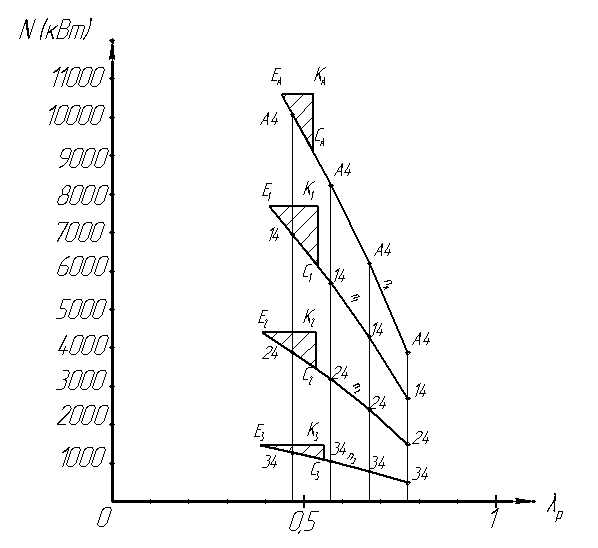 Табл.№7
Коэффициент усиления двигателя по положению рейки ТНВД. 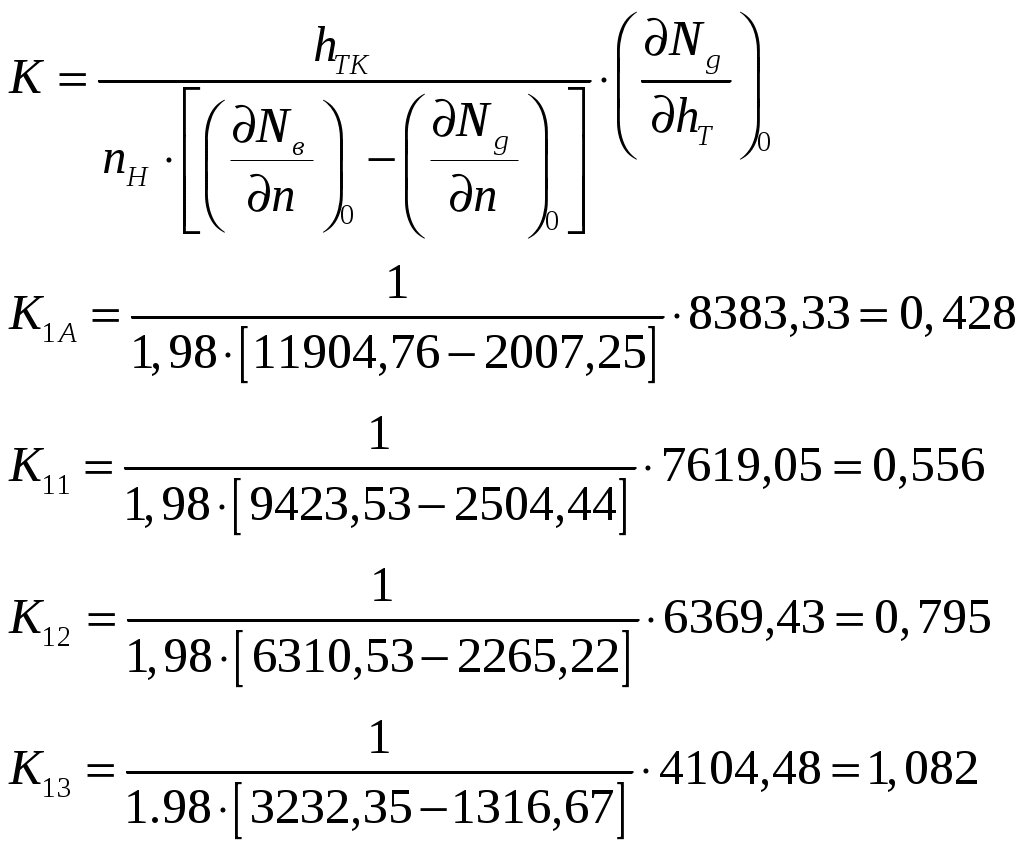 Определение коэффициента усиления двигателя по изменению внешней нагрузки. Для нахождения частной производной  , которая входит в выражение для определения коэффициента  перестроим винтовые характеристики в координатах “мощность, потребляемая винтом – относительная поступь винта”. Перестроение выполним в таблице №Исходная производная в точках установившихся режимов будет определяться как: 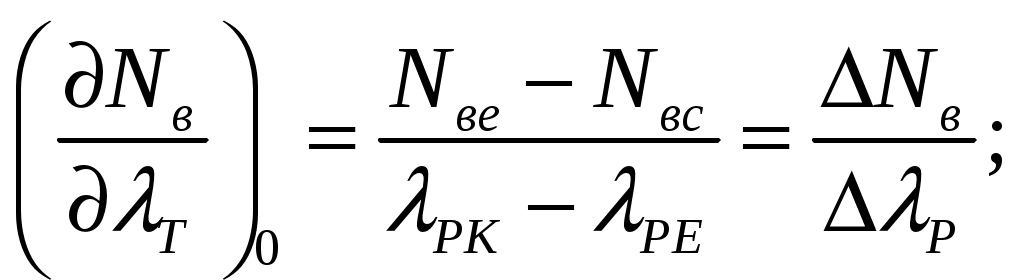 Ординаты винтовых характеристик. Табл.№8
Значения частной производной 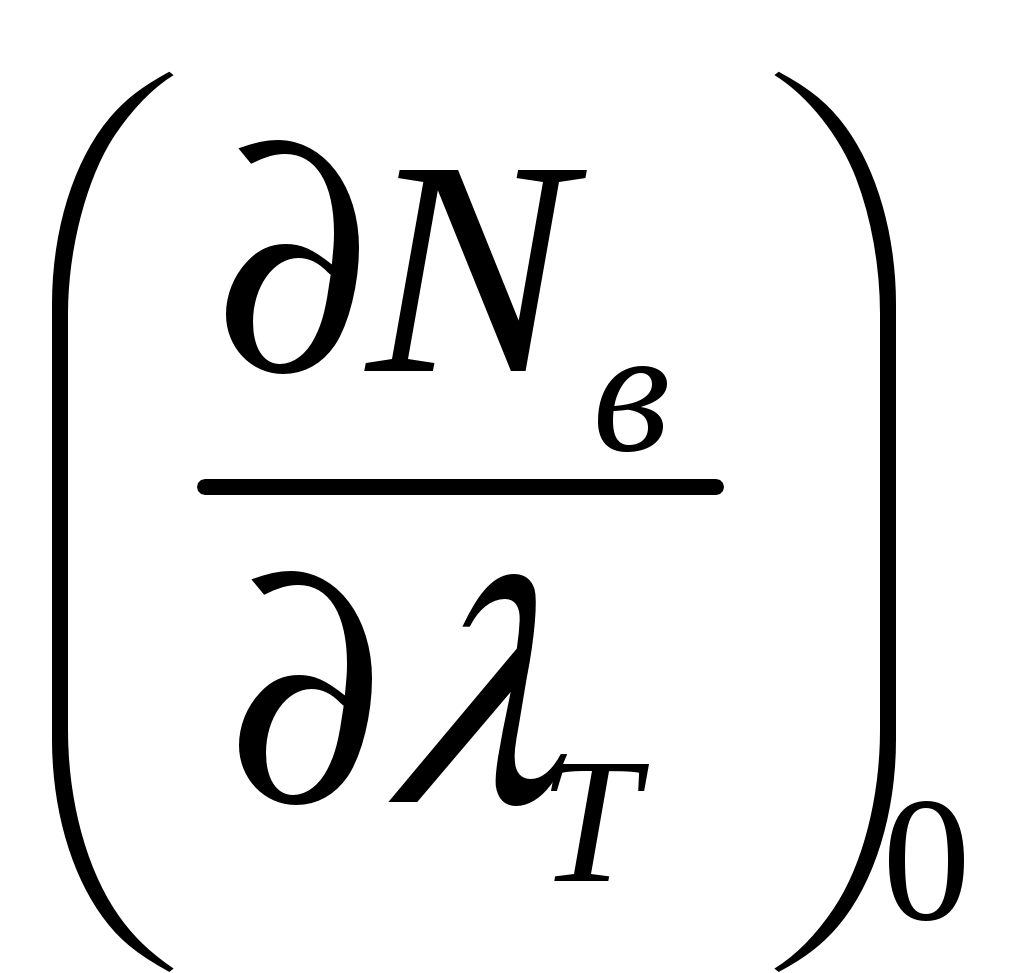 Вычисления частной производной выполним в таблице №9
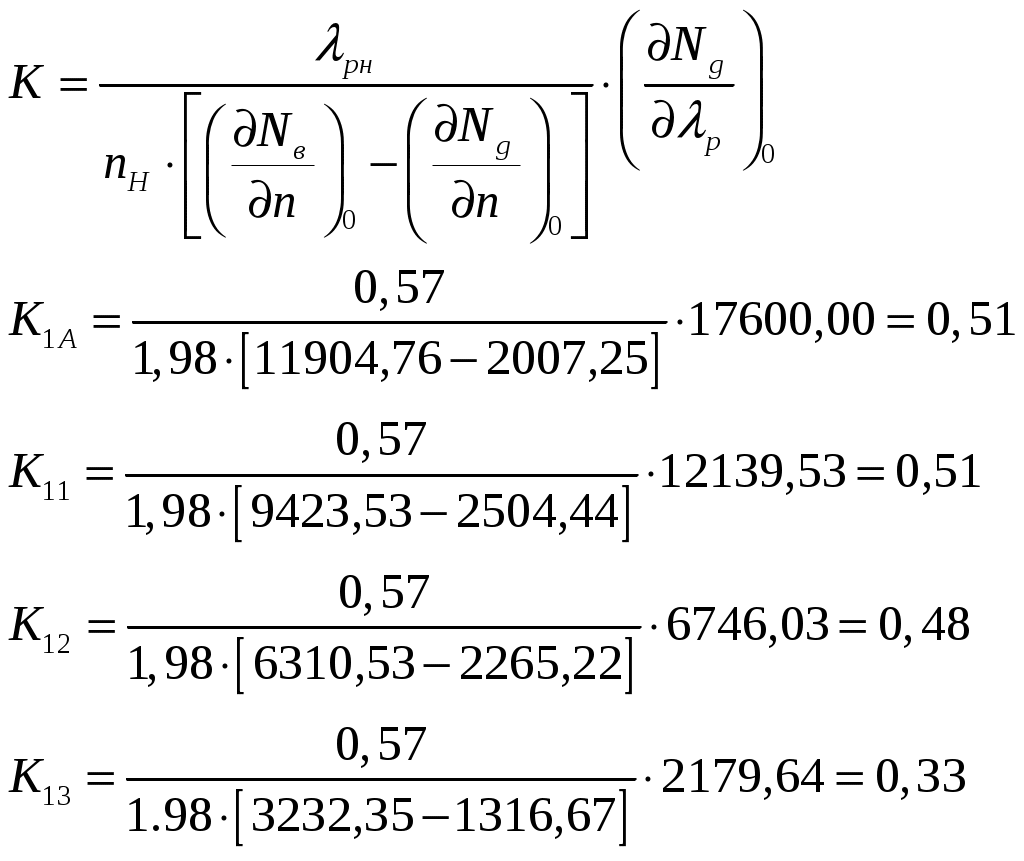 Получение винтовых характеристик двигателя. Численное значение коэффициентов уравнении динамики ГД на установившихся режимах работы сведем в таблицу Значения коэффициентов уравнения динамики двигателя. Табл.№10
Динамика регулятора скорости. Уравнение динамики измерителя. Уравнение динамики измерителя, представляющее аналитическую зависимость изменения во времени его выходной координаты 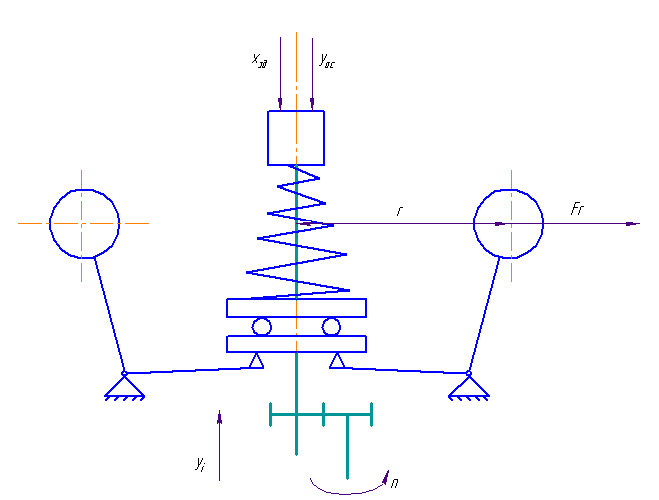 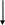, можно получить на основе принципа д,Ламбера, рассматривая все действующие силы, включая силы инерции. При движении на измеритель действуют следующие силы, приведенные к его муфте и показанные на рисунке.  E Fц 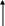 A Рис. Схема измерителя. - поддерживающая сила А, представляющая собой суммы приведенных к муфте центробежных сил грузов  ;-восстанавливающая сила  равная (или пропорциональная ) силе натяжения пружины задания;- сила веса G движущихся частей, приведенная к муфте; - сила сухого трения  ;-сила скоростного (или жидкостного) трения  , муфты, грузов, золотника и других деталей, вращающихся в масляной среде;- приведенная сила реакции струи  ;- сила инерции  всех движущихся масс;В соответствии с принципом д,Аламбера, обозначая приведенную массу всех движущихся деталей через  , можем записать. С целью упрощения будем пренебрегать силами веса, сухого трения, не уравновешенными силами, силами сопротивления и реакции струи в управляющем золотнике . При отмеченных допущениях, приняв за положительное направление движения муфты вверх, уравнение запишем так: Приведенная центробежная (поддерживающая) сила грузов А определяется суммарной массой грузов  , радиусом вращения их центра тяжести r и угловой скоростью вращения : Учитывая радиус r может быть однозначно выражен через выходную координату  , запишем: Приведенная восстанавливающая сила Е, равна силе натяжения пружины, является функцией перемещения муфты , координаты задания  , перемещения  под действием ЖОС и жесткости пружины С: Для цилиндрических пружин жесткость обычно принимается постоянной, для конических она представляет линейную функцию суммарной величины сжатия  отсюда  .Поэтому для общего случая  Приведенная сила жидкостного трения пропорциональна скорости движения  , где Д- коэффициент пропорциональности, определяемый экспериментальным путем.Будем рассматривать движение измерителя в приращениях относительно некоторого исходного равновесного состояния, тогда можем записать:  (1)Приращение сил 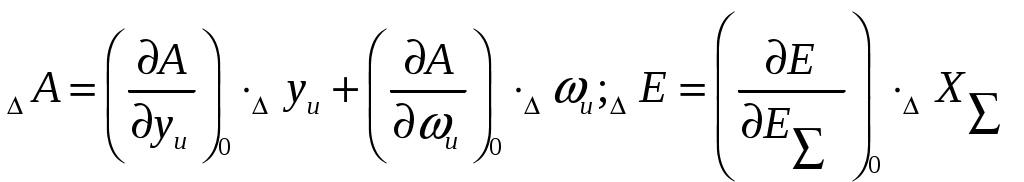 в линейном приближении получим, разложив функции А и Е в ряд Тейлора и сохранив при этом только члены первого порядка: Для цилиндрических пружин, обладающих постоянной жесткостью: 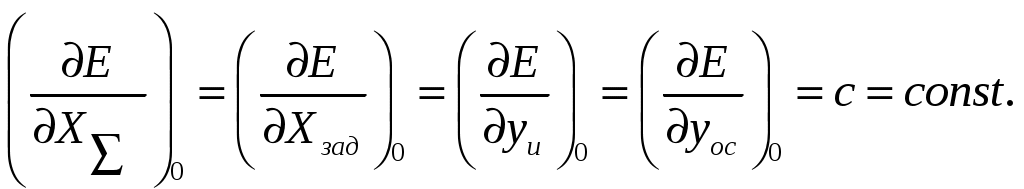 и для конических пружин угловой коэффициент 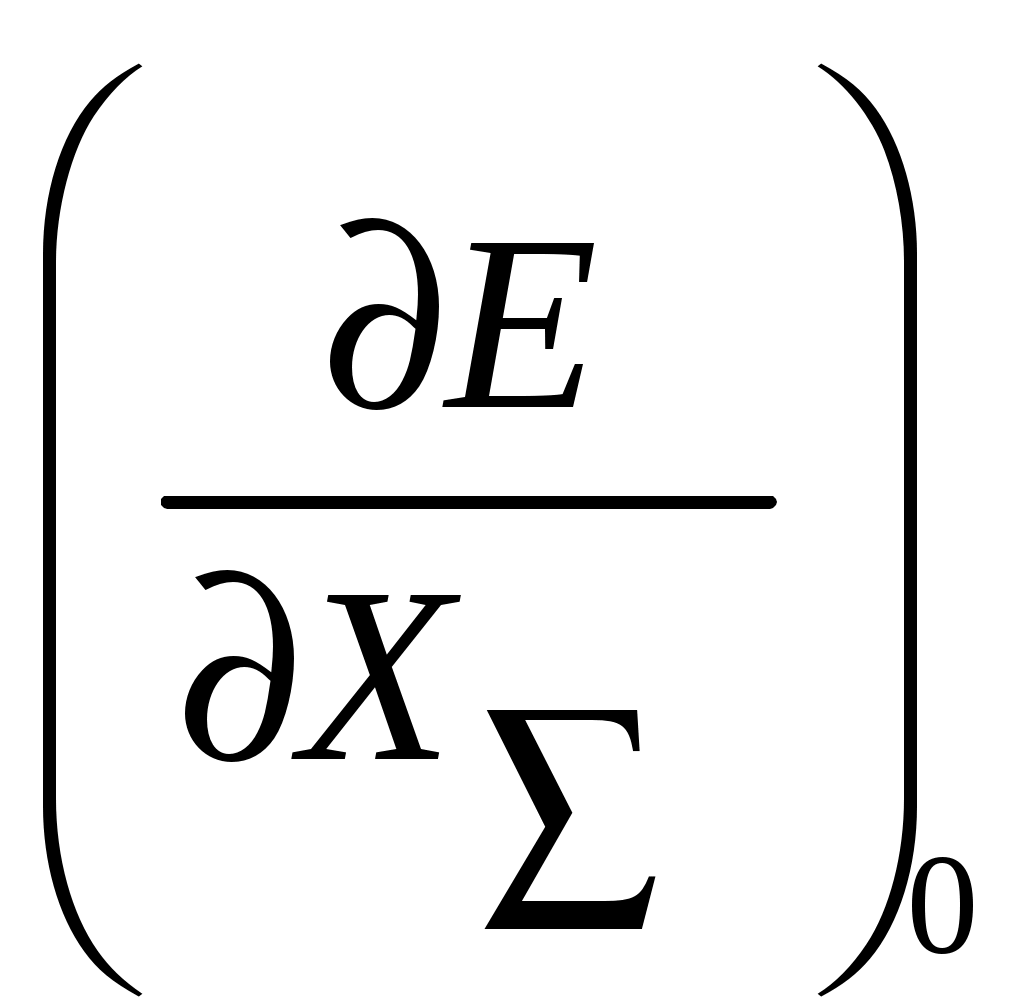 можем иметь различные значения. Он должен определятся в точке статической характеристики, соответствующий исходному режиму при суммарной величине сжатия  . Приращения силы жидкостного трения:  Уравнение движения измерителя в линейном приближении запишется так: 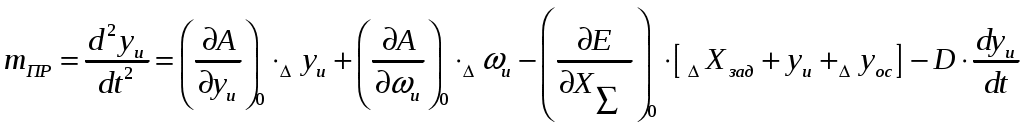 (2)При переходе к относительным коэффициентам, обозначив: |