ПРАВИЛА ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ. Правила приближенных вычислений
 Скачать 49.5 Kb.
|
|
ПРАВИЛА ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ Очень часто неопытные лица добиваются при вычислениях получения такой точности результата, которая совершенно не оправдывается точностью использованных данных. Это приводит к бесполезной затрате труда и времени. Рассмотрим такой случай. Пусть при решении задачи требуется вычислить плотность вещества  некоторого тела. Заданы масса тела  и его объём  . Важно отметить, что исходные данные имеют три значащие цифры.Справка. Значащими цифрами называют все цифры, кроме нуля, а также и нуль в двух случаях: 1) когда он стоит между значащими цифрами; 2) когда он стоит в конце числа и когда известно, что единиц соответствующего разряда в данном числе не имеется. Например, числа  ,  ,  имеют три значащих цифры.Без критического подхода к вычислениям можно для искомой плотности вещества получить такой результат  .Записанный результат имеет шесть значащих цифр. Однако достоверными могут считаться только три первые значащие цифры, что соответствует точности исходных данных. Следовательно, полученный результат необходимо округлить и представить в виде  .Приближенные вычисления следует проводить с соблюдением следующих правил. При сложении и вычитании приближенных чисел окончательный результат округляют так, чтобы он не имел значащих цифр в тех разрядах, которые отсутствуют хотя бы в одном из приближенных данных. Например, при сложении чисел 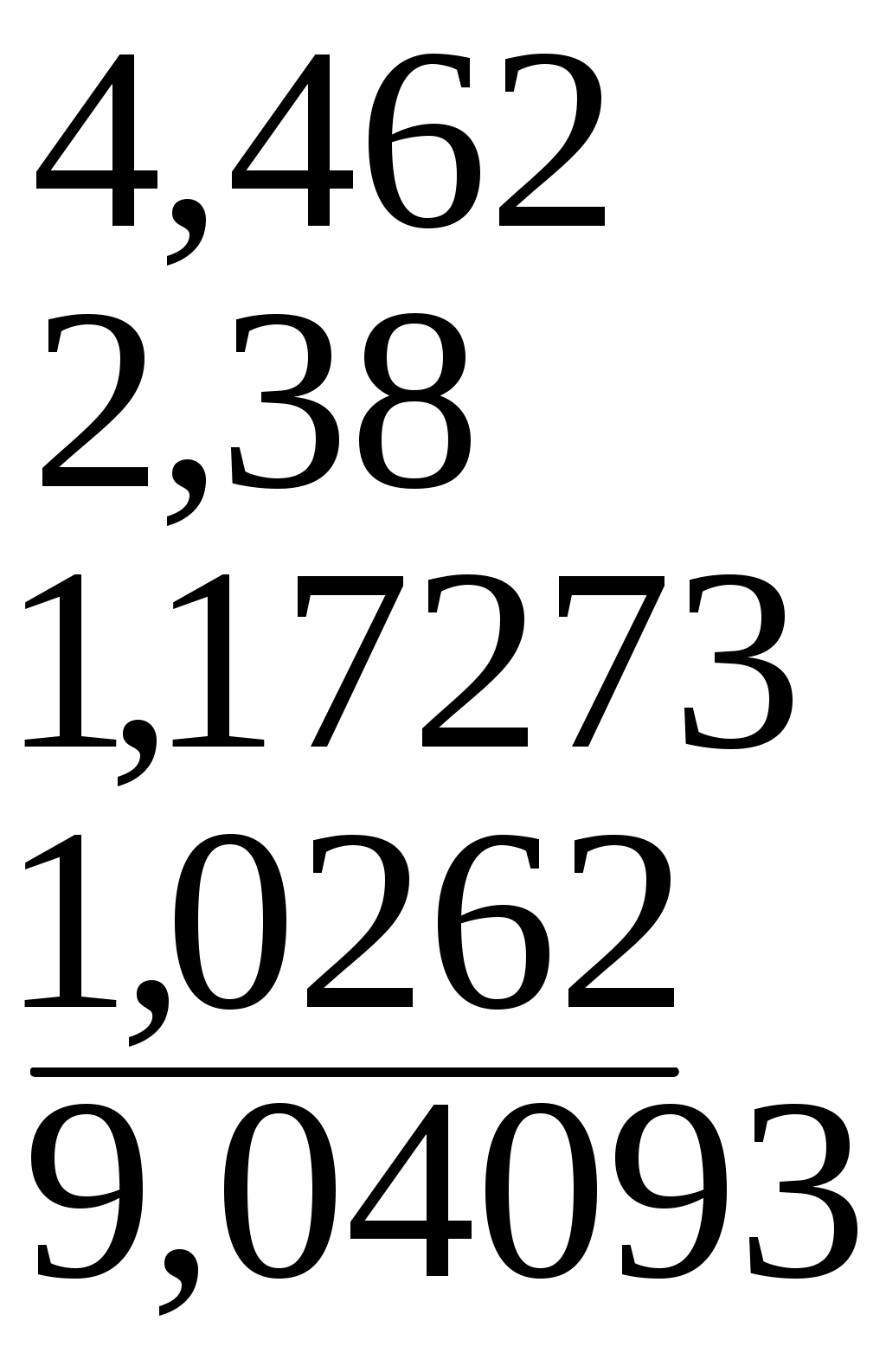 следует сумму округлить до сотых долей, приняв равной  .При умножении следует округлять сомножители так, чтобы каждый из них содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим числом таких цифр. Например, вместо вычисления выражения  следует вычислять выражение  .В окончательном результате следует оставлять такое же количество значащих цифр, какое имеется в сомножителях, после их округления. В промежуточных результатах надо сохранять на одну значащую цифру больше. Такое же правило соблюдается и при делении приближенных чисел. При возведении в квадрат или куб следует в степени брать столько значащих цифр, сколько их имеется в основании степени. Например,  .При извлечении квадратного или кубического корня в результате нужно брать столько значащих цифр, сколько их имеется в подкоренном выражении. Например,  .При вычислении сложных выражений следует применять указанные правила в соответствии с видом производимых действий. Например,  .Сомножитель  имеет наименьшее число значащих цифр – две. Поэтому результаты всех промежуточных вычислений должны округляться до трех значащих цифр: .После округления результата до двух значащих цифр окончательно получаем  .В заключение отметим, что указанные правила приближенных вычислений следует использовать не только при решении задач, но и при обработке результатов измерений в процессе выполнения лабораторных работ. Литература Чертов А.Г., Воробьёв А.А. Федоров М.Ф. Задачник по физике (с примерами решения задач и справочными материалами). - М.: Высшая школа,1973. |