Методические рекомендации по выполнению задания 8. Пример выполнения задания 8 Расчет плоской кинематически неопределимой рамы методом перемещений
 Скачать 353.12 Kb. Скачать 353.12 Kb.
|
|
Пример выполнения задания 8 Расчет плоской кинематически неопределимой рамы методом перемещений. Р Исходные данные: L2 = 6.0 м H1 = 4.0 м H2 = 6.0 м F = 8 кН q = 3 кН/м I1 : I2 =2:3 E = const ассчитать заданную раму методом перемещений. О 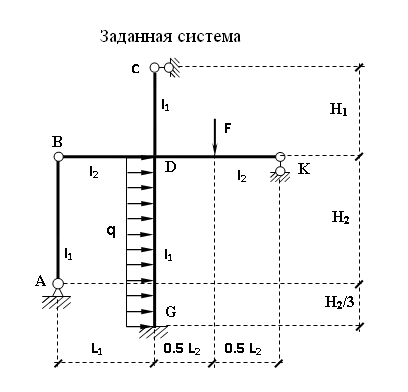 пределение степени кинематической неопределимости заданной рамы на рисунке. Степень кинематической неопределимости находится по формуле 2.1: nк = nу + nл = 1+1 = 2, nу = 1,так как «жесткий» узел - только узел D (все остальные узлы либо опорные, либо шарнирные); по формуле 2.2: n 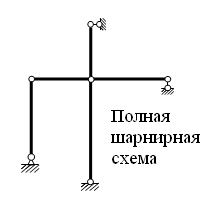 л = 3D – 2Ш - Соп = 3·5 – 2·4 – 7 = 1 (для полной шарнирной схемы). Таким образом, система дважды кинематически неопределима. Выбор основной и эквивалентной систем метода перемещений. Назначение неизвестных перемещений Z1 и Z2. Т 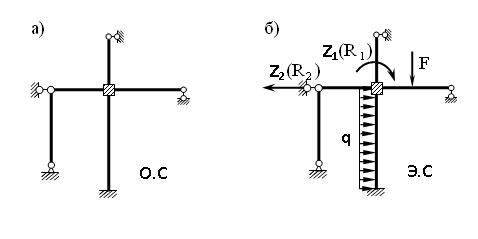 ак как система дважды кинематически неопределима, то в основную систему необходимо ввести две связи. Причем одна должна препятствовать угловому перемещению (nу = 1) – это заделка, введенная в «жесткий» узел, а другая должна препятствовать линейному смещению (nл=1) – это дополнительный опорный стержень, приложенный в направлении возможного линейного перемещения. Так как степень кинематической неопределимости равна двум, то уравнений в системе будет два. Система канонических уравнений будет иметь следующий вид: 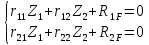 Построение единичных и грузовой эпюр изгибающих моментов. Для построения единичных и грузовой эпюр используется таблица 1 Приложение В. Для построения эпюр моментов необходимо первоначально определить погонные жесткости для каждого участка рамы. Для этого пронумеруем каждый стержень рамы. Погонная жесткость определяется по формуле i=EI/L; так как I1 : I2 =2:3, следовательно, примем I1 = 2I , I2 = 3I. i1 = EI1 / H2= 2EI / 6 = EI / 3 i2 = EI2 / L1 = 3EI/ 4 i3 = EI1 / H1= 2EI/ 4 = EI / 2 i4 = EI1 / (4H2 / 3)=2EI / 8 = EI / 4 i5 = EI2 / L2 = 3EI / 6 = EI / 2 Т 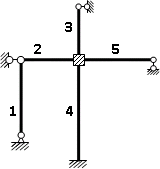 еперь по таблице, исходя из деформированного состояния системы, построим эпюры: Первую эпюру строим от поворота первой введенной заделки на единичный угол. На рисунке а изображено деформированное состояние системы, а на рисунке б первая единичная эпюра: 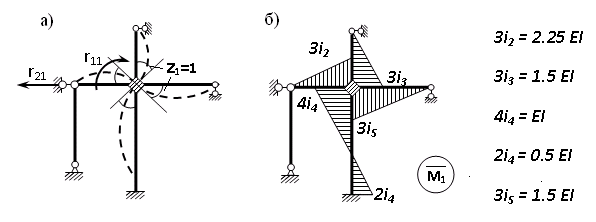 В 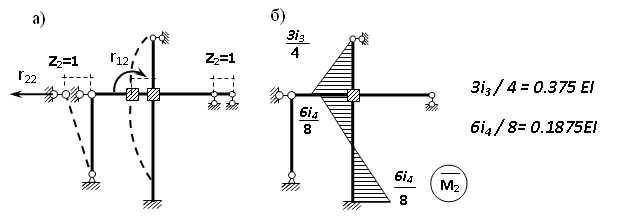 торую эпюру строим от линейного смещения узлов на единицу. На рисунке а изображено деформированное состояние системы, а на рисунке б вторая единичная эпюра: Грузовую эпюру строим от заданной внешней нагрузки, при этом эпюра строится только на участках, к которым приложена внешняя нагрузка. На рисунке а изображено деформированное состояние системы, а на рисунке б грузовая эпюра: 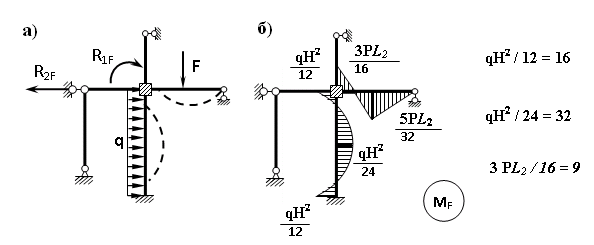 В 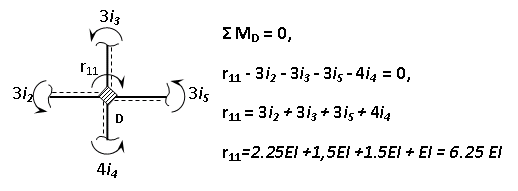 ычисление коэффициентов и свободных членов канонических уравнений (статический способ).    Н 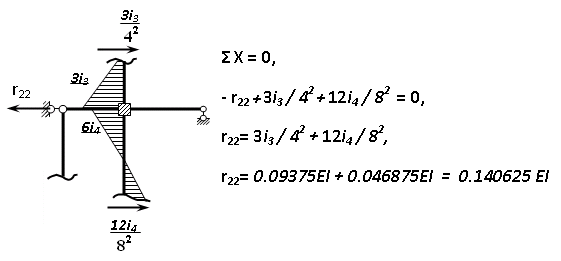 а основании теоремы о взаимности перемещений должно выполняться условие r12=r21. 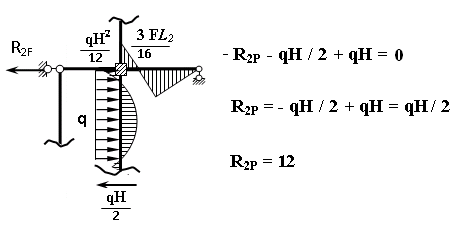 Построение суммарной единичной эпюры изгибающих моментов (формула 2.13): 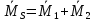 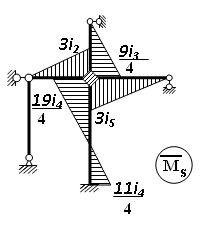 Выполним универсальную проверку единичных коэффициентов (формулы 2.14-2.15): 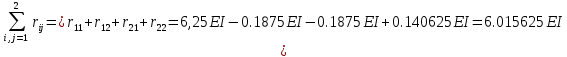 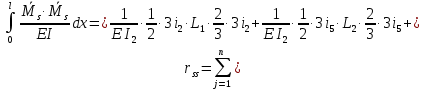 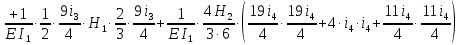 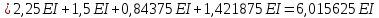 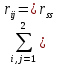 Выполнена универсальная проверка, следовательно, единичные коэффициенты найдены верно. Аналогично выполняется проверка грузовых коэффициентов. Составим систему канонических уравнений: 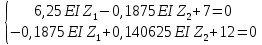 Умножим первое уравнение на 16, а второй уравнение на 64, получим более простую систему уравнений: 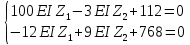 Решая данную систему, получим: Z1 = - 3,833/EI Z2 = - 90,444/EI Делаем проверку найденного решения, т.е. подставляем полученные значения Z1 и Z2 в канонические уравнения: 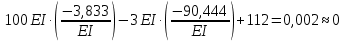 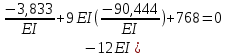 Условие выполнено, значит, решение найдено верно. Построение окончательной эпюры изгибающих моментов (формула 2.8) 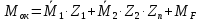 Для этого возьмем первую единичную эпюру и все ее значения (ординаты) умножим на действительную величину Z1=-3,833/EI, при этом жесткости сократятся и останутся только числовые значения. Аналогично возьмем вторую единичную эпюру и все ее значения (ординаты) умножим на действительную величину Z2=-90,444/EI, при этом жесткости сократятся и останутся только числовые значения. Полученные таким образом эпюры сложим вместе с грузовой эпюрой по характерным точкам всей системы. 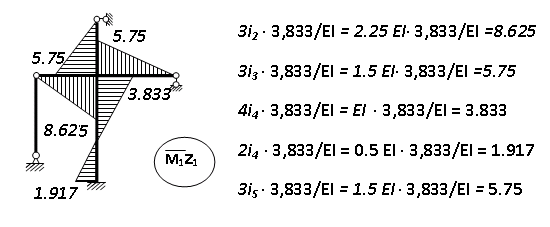 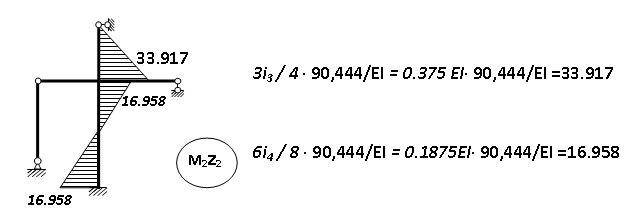 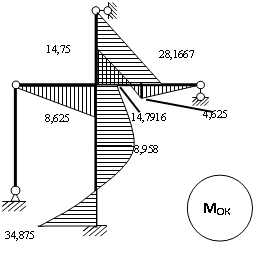 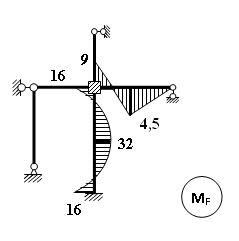 Проверяем правильность построения эпюры Мок. Статическая проверка: 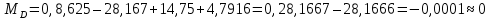 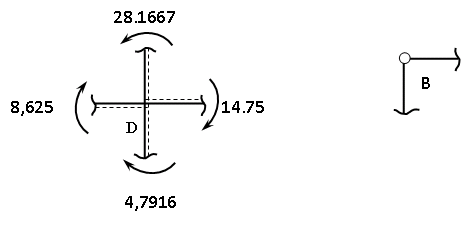 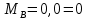 Статическая проверка выполнена, следовательно, эпюра Мок построена верно. П 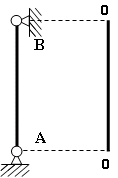 Т.к. на участке АВ отсутствуют изгибающие моменты и внешняя нагрузка , то эпюра поперечных сил на этом участке будет очерчена нулевой линий. остроение эпюры поперечных сил на основании построенной эпюры изгибающих моментов Мок 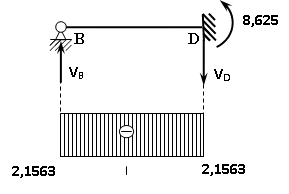 МВ = 0, VС·4 - 8,625 =0, VС = 2,1563 кН МD = 0, VВ·4 - 8,625 =0, VВ = 2,1563 кН Y = 0, VВ - VD = 0, 0 = 0 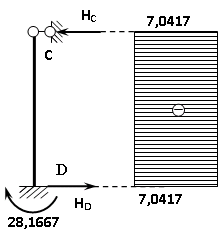 МD = 0, HС·4 +28,1667 = 0, HС = 7,0417 кН МС = 0, -HD·4 +28,1667 = 0, HD = 7,0417 кН X = 0, HD - HС =0, 0 = 0 МD = 0, - 4,7916 - 34,875 - q·8·4 + НЕ·8 = 0, НЕ = 16,9583 кН МE = 0, - 4,7916 - 34,875 + q·8·4 - НD·8 = 0, НD = 7,0417 кН Х = 0, -НE - НD + q·8 = 0, 0 = 0   МD = 0, VF·6 -14,75 + F·3 =0, VF = -1,5417 кН – значит направление реакции выбрано неверно, поэтому меняем его на противоположное. МF = 0, VD·6 -14,75 - F·3 =0, VD = 6,162 кН Y = 0, VD + VF + F = 0, 0 = 0 Э  пюра поперечных сил в общем виде будет иметь следующий вид:  Х = 0, NВD = 0, Y = 0, -NАВ + 2,1563 = 0 NAB = 2,1563 кН Построение эпюры продольных (нормальных) сил N , на основании построенной эпюры поперечных сил: 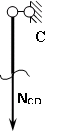 Y = 0 NCD = 0 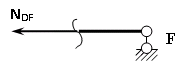 X = 0 NDF = 0 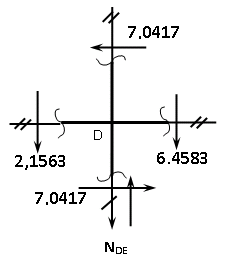 Y = 0, - NDE – 2,1563 – 6,4583 = 0 NСD = -8,6146 кН- направлено в противоположную сторону. X = 0, - 7,0147 + 7,0147 = 0, 0 = 0 Эпюра продольных сил N в общем виде будет иметь следующий вид: 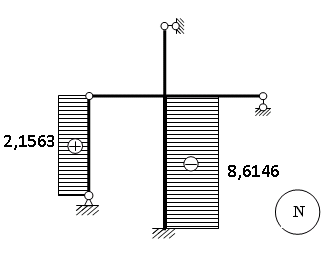 Согласно построенным эпюрам M, N, Q определяем опорные реакции рамы и составляем условие статического равновесия рамы в целом. Для этого используем формулы статического равновесия системы в целом 2.19-2.21. Вертикальные опорные реакции VA,VE определяем по эпюре продольных сил N, горизонтальные реакции HA, HE, HC и вертикальную реакция VF определяем по эпюре поперечных сил Q, а реакцию ME определяем по эпюре изгибающих моментов М. 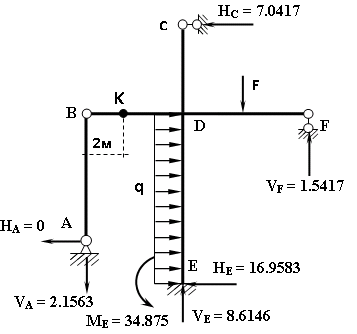 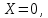 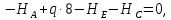 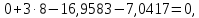 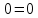 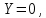 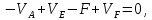 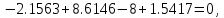 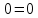 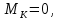  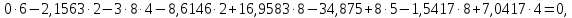 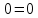 Вывод: Проверки выполнены, значит, рама рассчитана верно, эпюры M, N, Q построены правильно. |
