билеты физика мифи 1 семестр. Принцип относительности Галилея. Преобразования Галилея
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Первый закон Ньютона – В инерциальной системе отсчета скорость тела = const, если на тело не действуют силы (другие тела) или сумма этих сил = 0. В неинерциальной системе отсчета 1 закон Ньютона не выполняется. Инертность — свойство тела в большей или меньшей степени препятствовать изменению своей скорости относительно инерциальной системы отсчёта при воздействии на него внешних сил. Масса - мера инертности тела (сопротивления воздействию). Свойства массы: Величина аддитивная (т.е. сумма системы = сумме масс, её составляющих) Масса тела постоянна. (т.е. не изменяется при движении) Сила — векторная физическая величина, являющаяся мерой воздействия на данное тело других тел Равнодействующая сила – это сила, действие которой заменяет действие всех сил, приложенных к телу. Или, другими словами, равнодействующая всех сил, приложенных к телу, равна векторной сумме этих сил. Вопрос 7 Динамика - раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. Динамика - количественное описание взаимодействия тел, определяющего характер их движения. Сила - это физическая величина, характеризующая изменение скорости движения тела. Она носит векторный характер, т. е. выражается вектором. Иначе сила - это скорость изменения импульса тела F = dP / dt, P = mv - импульс тела, m - масса тела, v - скорость, с которой движется тело. Если на данное тело действует одновременно несколько сил, то их действие на движение тела можно заменить действием одной силы). Такую замену называют сложением сил. Данные силы называют слагающими или составляющими, а заменяющую их силу — их суммой или равнодействующей. Равнодействующая уравновешивающихся сил, например, двух сил, равных по величине и противоположных по направлению, равна нулю. *Второй закон Ньютона В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. a – ускорение материальной точки; F - равнодействующая всех сил, приложенных к материальной точке; m - масса материальной точки. Третий закон Ньютона. Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: Основное уравнение динамики материальной точки в случае, когда на точку действуют n сил, имеет вид: Вопрос 9 Принцип относительности Галилея: Механические явления протекают одинаково во всех инерциальных системах отсчета, т. е. описывающие их законы динамики одинаковы. Поэтому все инерциальные системы отсчета равноправны. Это значит, что уравнения, выражающие законы механики, не меняются при преобразованиях Галилея. Преобразования Галилея заключаются в преобразовании координат и времени t движущейся материальной точки при переходе от одной инерциальной системы отсчета к другой: Для координаты x это выражается так: Здесь и - радиус-векторы, и - координаты точки в двух инерциальных системах отсчета, а υ – относительная скорость движения этих двух инерциальных систем отсчета. Время не изменяется при переходе из одной инерциальной системы отсчета в другую. В любой последующий момент времени положение некоторой точки А, движущейся относительно обеих систем координат, определяется в системе K радиус-вектором , а в системе K´ - радиус-вектором . Вектор, соединяющий начало координат О неподвижной системы координат с началом координат О´ подвижной системы, равен вектору перемещения системы K´ относительно K: Из этого уравнения вытекает закон сложения скоростей: где - скорости точки относительно систем K и K´ соответственно. 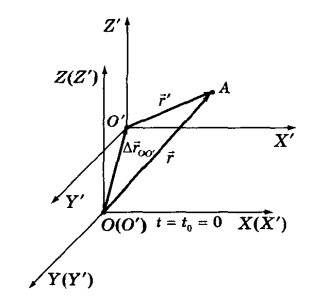 Галилей на основании наблюдений сформулировал классический принцип относительности, согласно которому законы механики одинаковы в любых инерциальных системах отсчета. То есть, уравнения движения относительно любых инерциальных систем совпадают друг с другом. Это значит, что уравнение mw = F эквивалентно уравнению m´w´ = F´. Из принципа Галилея следует, что F = F´, т. е. силы, действующие на точку, неизменны при переходе от одной инерциальной системы к другой, также инерциальной системе. Следовательно, все величины, входящие в уравнение Ньютона, не изменяются при преобразовании от одной инерциальной системы к другой инециальной системе. Вопрос 9 Вес − это сила, с которой любое тело вследствие притяжения Земли действует на опору или подвес. Вес тела − векторная физическая величина, которую обозначают буквой P. Вес покоящегося, а также равномерно и прямолинейно движущегося (относительно Земли) тела по своему численному значению равен действующей на него силе тяжести: P=Fт=mg где m − масса, g − ускорение свободного падения. Сила тяжести — сила, действующая на любое материальное тело, находящееся вблизи поверхности Земли или другого астрономического тела. По определению, сила тяжести на поверхности планеты складывается из гравитационного притяжения планеты и центробежной силы инерции, вызванной суточным вращением планеты. Вес и сила тяжести приложены к разным объектам: вес P приложен к опоре или подвесу, а сила тяжести Fт − к телу. Вес и сила тяжести имеют различную физическую природу. Сила тяжести возникает вследствие взаимодействия тела и Земли. Вес тела возникает в результате взаимодействия тела и опоры (подвеса). Опора (подвес) при этом деформируется, что приводит к появлению силы упругости. Из третьего закона Ньютона следует, что вес тела, то есть сила, с которой тело давит на опору (или растягивает подвес), совпадает по величине с силой, действующей со стороны опоры на данное тело. Сила, с которой опора давит на находящееся на ней тело, называется силой реакции опоры. Обозначив силу реакции опоры N, мы можем записать: N = −P Полученная формула является более общей, чем P=mg, так как она справедлива и в том случае, когда тело вместе с опорой совершает ускоренное движение. Силой трения называют силу, которая возникает при движении одного тела по поверхности другого. Она всегда направлена противоположно направлению движения. Сила трения прямо пропорциональна силе нормального давления на трущиеся поверхности и зависит от свойств этих поверхностей. Сухое трение возникает между поверхностями твердых тел в отсутствие смазки. Сухое трение, в свою очередь, подразделяется на трение скольжения и трение качения. Установлено, что максимальная сила трения покоя не зависит от площади соприкосновения тел и приблизительно пропорциональна модулю силы нормального давления N: μ0 – коэффициент трения покоя, зависящий от природы и состояния трущихся поверхностей. Когда модуль внешней силы, а, следовательно, и модуль силы трения покоя превысит значение F0, тело начнет скользить по опоре – трение покоя Fтр.пок сменится трением скольжения Fск:
где μ – коэффициент трения скольжения. Трение качения возникает между шарообразным телом и поверхностью, по которой оно катится. Сила трения качения подчиняется тем же законам, что и сила трения скольжения, но коэффициент трения μ ; здесь значительно меньше. Коэффицент трения - количественная характеристика силы, необходимой для скольжения или движения одного материала по поверхности другого. Если обозначить вес предмета как N, а коэффициент трения - m, то сила (F), необходимая для движения предмета по ровной поверхности без ускорения, равна F = mN. Коэффициент трения покоя определяет силу, необходимую для начала движения; коэффициент кинетического трения (трения движения) определяет (меньшую) силу, необходимую для поддержания движения. Вопрос 10 Импульсом материальной точки называют величину равную произведению массы точки на ее скорость. Обозначим импульс буквой p⃗. Тогда p⃗ = mυ⃗. Из этой формулы видно, что импульс — векторная величина. Импульс системы P∑→ материальных точек массами m1, m2, m3, …, имеющих скорости V1→, V2→, V3→, …, определяется соотношением: P∑→=m1V1→+m2V2→+m3V3→+…,то есть P∑→=P1→+P2→+P3→+…, где Pk→ — импульс k-й материальной точки. Т.е. это сумма импульсов материальных точек этой системы. Система называется замкнутой, если на неё не действуют внешние силы или сумма внешних сил = 0. Вывод закона сохранения импульса. Второй закон Ньютона выражается формулой . Ее можно записать иным способом, если вспомнить, что ускорение равно быстроте изменения скорости тела. Для равноускоренного движения формула будет иметь вид: Если подставить это выражение в формулу, получим: Эту формулу можно переписать в виде: В правой части этого равенства записано изменение произведения массы тела на его скорость. Произведение массы тела на скорость является физической величиной, которая называется импульсом тела. Обозначим массы этих двух тел через m1 и m2, а их скорости относительно какой-либо системы отсчета через и . Через некоторое время t в результате взаимодействия тел их скорости изменятся и станут равными и . Подставив эти значения в формулу, получим: Следовательно, Изменим знаки обеих частей равенства на противоположные и запишем в виде В левой части равенства – сумма начальных импульсов двух тел, в правой части – сумма импульсов тех же тел через время t. Суммы равны между собой. Таким образом, несмотря на то. что импульс каждого тела при взаимодействии изменяется, полный импульс (сумма импульсов обоих тел) остается неизменным. Вопрос 11 Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой. Работа силы на конечном перемещении равна сумме ее работ на элементарных участках. Работа силы на конечном перемещении М1М0 равняется интегралу вдоль этого перемещения от элементарной работы. Работа силы на перемещении М1М2 изображается площадью фигуры, ограниченной осью абсцисс, кривой и ординатами, соответствующими точкам М1 и М0. Единица измерения работы силы и кинетической энергии в системе СИ 1 (Дж). Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом: 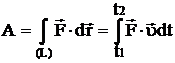 Если = const, то А= × . Работой постоянной силы называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы и перемещения : Выражение показывает, что работа является скалярной величиной и может иметь положительное или отрицательное значение в зависимости от знака косинуса угла . Работа, совершаемая силой , положительна, если угол между вектором силы и вектором перемещения меньше 90°. Работа силы упругости — работа, совершаемая силой упругости при изменении деформации пружины от некоторого начального значения x1 до конечного значения x2 Вывод формулы работы силы упругости (через интеграл)  Коэффициент жесткости пружины k называется жесткостью тела, он зависит от материала, из которого тело изготовлено, а также от его геометрических размеров и формы. Жесткость выражается в ньютонах на метр (Н/м). Сила упругости зависит только от изменения расстояний между взаимодействующими частями данного упругого тела. Работа силы упругости не зависит от формы траектории и при перемещении по замкнутой траектории равна нулю. Поэтому силы упругости является потенциальными силами. Работа сил гравитационного поля при сближении двух материальных точек равна уменьшению потенциальной энергии тяготения А = – DП = – (П2 – П1) = П1 – П2. Вопрос 12 Мощность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. = 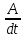 – средняя мощность. {P} = Вт [ватты] скалярная физическая величина. – средняя мощность. {P} = Вт [ватты] скалярная физическая величина.P= 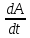 = = 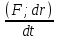 =(F; =(F; ) = (F;V) ) = (F;V)Кинетическая энергия. dA = F dr = 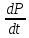 =m * =m * 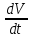 * dr / * dr /  / = mV*dV /внесли V под знак дифференциала/ = / = mV*dV /внесли V под знак дифференциала/ = 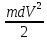 dA=d(  ) Тогда Ek = ) Тогда Ek =  ; dA=dFk ; dA=dFkВопрос 13 Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке (поле силы тяжести Земли). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы. Стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от траектории, а зависит только от положения этих точек, называется потенциальным, а сами силы – консервативными (F тяж, F упр). Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными (F трения). Свойства консервативных сил: Таким образом, потенциальная сила всегда направлена в сторону уменьшения потенциальной энергии. Вопрос 14 Потенциальная энергия частицы в поле. Поле остающееся постоянным во времени называют стационарным. Стационарные силовые поля, в которых работа не зависит от пути между точками 1 и 2 называют консервативными. Если работа не зависит от траектории, а зависит только от начального и конечного положения материальной точки, то можно сопоставить полю некоторую функцию координат.  перемещение частицы из точки 1 в точку 2: А12 = Еп1-Еп2 Выражение, стоящее справа, – разность потенциальной энергии частицы в начальном и конечном положении. Это соотношение позволяет найти выражение для Еп для любого стационарного поля потенциальных сил. Для этого нужно вычислить работу, совершаемую силами поля на любом пути между двумя точками и представить ее в виде разности некоторой функции, которая и есть потенциальная энергия. А представить разностью можно через интеграл Т.е. перемещение частицы из точки 1 в точку 2: А12 = Еп1-Еп2 Выражение, стоящее справа, – разность потенциальной энергии частицы в начальном и конечном положении. Это соотношение позволяет найти выражение для Еп для любого стационарного поля потенциальных сил. Для этого нужно вычислить работу, совершаемую силами поля на любом пути между двумя точками и представить ее в виде разности некоторой функции, которая и есть потенциальная энергия. А представить разностью можно через интеграл Т.е.Е1-Е2= 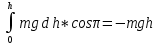 Е1(0)-Е2(h) = -mgh т.к. Е(0)=0 -Е2(h)= - mgh Е(h)=mgh Е1(0)-Е2(  )= - )= - 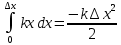 -Е2(  )= )=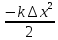 ; Е2( ; Е2( )= )= Связь между потенциальной энергией и силой. Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы F, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии Eп. Для установления связи вычислим элементарную работу dA, совершаемую силами поля при малом перемещении dr тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой r. Эта работа равна dA=Fdr= - dE где F- проекция силы на направление r. Поскольку в данном случае работа совершается за счет запаса потенциальной энергии E, она равна разности потенциальной энергии –dЕ на отрезке оси. А отсюда получаем: F=  ; В декартовой системе координат F = - градиенту энергии. Т.е. ; В декартовой системе координат F = - градиенту энергии. Т.е. F= 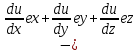 ); );Т.к. Е= mgh, где за h возьмем, к примеру, ось y, тогда F= 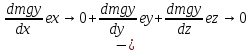 ); = - mgy По оси y. ); = - mgy По оси y.Билет 15 Полная механическая энергия частицы – энергия механического движения и взаимодействия, равная умме кинетической и потенциальной энергий: E = Ek + Ep Из выражения Если сторонние силы отсутствуют, то полная механическая энергия частицы в стационарном поле консервативных сил остается постоянной. Билет 16 Кинетическая энергия механической системы - это энергия механического движения рассматриваемой системы. Потенциальная энергия - механическая энергия системы тел, которая определяется характером сил взаимодействия между телами этой системы и их взаимным расположением. Напомню: работа, совершаемая действующими в системе силами при перемещении тела из точки 1 в 2, не зависит от траектории, по которой это перемещение произошло. [билет 14]. В случае, если работа силы зависит от траектории перемещения тела из одного положения в другое, то такая сила называется диссипативной; примером диссипативной силы является сила трения. Собственная потенциальная энергия системы частиц. Е =  . Где mV - частица (со своей массой и потенциалом) в закрытой системе. Для двух частиц потенциал V2 вызван массой m1, а потенциал V1 вызван массой m2. Т.е. одно тело действует на второе и наоборот. Вместо mV можно подставить любую функцию, описывающую движение частицы, но Е в любом случае будет суммой их взаимодействий. . Где mV - частица (со своей массой и потенциалом) в закрытой системе. Для двух частиц потенциал V2 вызван массой m1, а потенциал V1 вызван массой m2. Т.е. одно тело действует на второе и наоборот. Вместо mV можно подставить любую функцию, описывающую движение частицы, но Е в любом случае будет суммой их взаимодействий.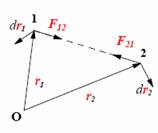 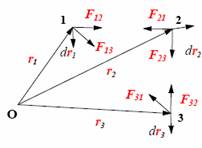 Для двух частиц: Классификация сил. По характеру взаимодействия: Массовые (объёмные) силы обусловлены взаимодействием материальных тел на расстоянии, они приложены к каждой точке тела (распределены по всему его объёму). К массовым силам относятся силы гравитационного и электромагнитного взаимодействия. Обычно из чисто формальных соображений к ним добавляют силы инерции (для сил инерции невозможно указать конкретный материальный источник). Поверхностные силы приложены к участкам поверхности и являются результатом взаимодействия материальных тел при непосредственном контакте. В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные силы подразделяются на сосредоточенные и распределённые. К первым относятся нагрузки, площадь приложения которых несоизмеримо меньше площади поверхности тела. Таковыми являются, например, сила нормального давления и сила трения между колесом тележки и подкрановой балки, а также силы взаимодействия балки с опорами. Билет 17 Преобразования Лоренца − преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. (Инерциальная система отсчёта – система отсчёта, движущаяся прямолинейно с постоянной скоростью v). Если инерциальная система отсчёта K' движется относительно инерциальной системы отсчёта K с постоянной скоростью v вдоль оси x, то преобразования Лоренца имеют вид c - скорость света в вакууме, β = v/c. Формулы, выражающие x', y', z', t' через x, y, z, t получаются из соотношения (1) заменой v на -v.
При v < c преобразования Лоренца переходят в преобразования Галилея: x = x' + vt, y = y', z = z', t = t'. Формулы преобразования скорости: 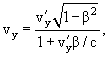 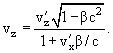 Сложение скоростей Тело движется в системе K’, которая сама движется относительно системы K. Скорость движения этого теля относительно неподвижной системы отсчёта K равна векторной сумме скорости этого тела относительно подвижной системы отсчета K’ и скорости той точки подвижной системы отсчёта, в которой в данный момент времени находится тело (относительно неподвижной системы). Длина стержня в системе К: Из преобразований Лоренца: 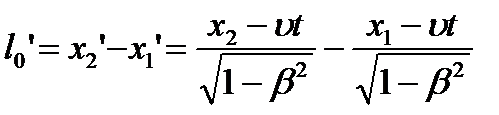 Линейные размеры тела наибольшие в той инерциальной системе отсчёта, отн-но которой тело покоится. Длительность событий в разных системах отсчёта. Пусть в некоторой точке (с координатой х), покоящейся относительно системы К, происходит событие, длительность которого 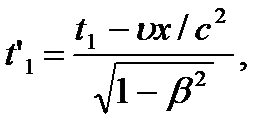  Представляя второе в первое получим: Отсюда видно, что Билет 18 v – скорость частицы, а m – Ньютоновская масса. В случае малых скоростей эти соотношения дают обычный результат В опытах с телами, двигающимися быстрее скорости света этот закон не действует, он заменяется на 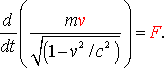 - уравнение в релятивистской механике. - уравнение в релятивистской механике.Кинетическая энергия релятивистской частицы Правила кинетической энергии, которые действовали в ньютоновской механике, верны также и для релятивистской частицы. Необходимо только видоизменить формулу кинетической энергии частицы  Это и есть формула релятивистской кинетической энергии. Билет 19 Релятивистское выражение для импульса. Найдем такое выражение для импульса, чтобы закон сохранения импульса был неизменным к преобразованиям Лоренца при любых скоростях (как мы уже говорили, уравнения Ньютона не неизменны к преобразованиям Лоренца и закон сохранения импульса в k выполняется, а в k' – нет). Ньютоновское выражение для импульса или . В выражении m – постоянная величина – масса частицы в системе k (собственная масса частицы), неизменная величина; dt – интервал времени по часам неподвижного наблюдателя. Если заменить dt на – собственное время частицы, тоже неизменную величину, то получим неизменное выражение для импульса . Преобразуем это выражение с учетом того, что: или Это и есть релятивистское выражение для импульса. Следует, что никакое тело не может двигаться со скоростью большей или даже равной скорости света (при υ→c знаменатель стремится к нулю, тогда p→∞ , что невозможно в силу закона сохранения импульса). Масса покоя. Закон взаимосвязи массы и энергии. Энергия покоя частицы. Связь между энергией и импульсом частицы. Вопрос 20 Колебательными называют движения, которые в точности или приблизительно повторяются через одинаковые промежутки времени. X(t)=Acos(w0t+µ), где А – амплитуда колебаний, µ - начальная фаза колебаний(определяется тем, ка тело вывели из состояния покоя), w0 – собственная частота колебаний. (w0t+µ) – фаза колебаний.  Свободные колебания — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии при отсутствии внешних воздействий. (толкнули и отпустили). Свободные колебания — это колебания колебательной системы, совершаемые благодаря периодическому внешнему воздействию. (постоянно толкают) Автоколебания - незатухающие колебания, которые могут существовать в какой-либо системе при отсутствии переменного внешнего воздействия, причём амплитуда и период колебаний определяются свойствами самой системы. /Автоколебательные системы – системы, которые сами определяют периодичность внешнего воздействия (механические часы)/ Параметрическими называют колебания, при которых один из параметров физической системы периодически изменяется. /Параметрический резонанс – заключается в совершенном в такт с колебаниями периодическом изменении какого-либо параметра системы, вследствии чего само явление – параметрический резонанс. Вопрос 21 Гармонические колебания - колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса. Рассмотрим массу, которая колеблется на пружине. Если амплитуда колебаний мала, то координата x массы по вертикальной оси изменяется по гармоническому закону: x= Asin(wt + j) где A - амплитуда колебаний, t - время, j – фаза колебаний,w- угловая частота колебаний,w= 2pf=2p /T, f - частота колебаний, T - период колебаний. Найдём период колебаний T пружинного маятника, состоящего из грузика массой m и пружины жёсткостью k. Если грузик смещён из нулевого положения (в котором пружина не деформирована) на расстояниеx, то на грузик со стороны пружины будет действовать сила-kx. На грузик действует сила тяжести mg. Согласно второму закону Ньютона, сумма всех сил, приложенных к грузику, равна ma, где a - ускорение. Дифференциальное уравнение для пружинного маятника: md2x/dt2 = -kx + mg, где g- ускорение свободного падения в гравитационном поле,d2x/dt2 - вторая производная координаты x по времени t. Это уравнение имеет следующее решение: x = Asin[(k/m)1/2t + j] + mg/k Мы можем видеть из этой формулы, что период колебаний равен T = 2p(m/k)1/2 и, соответственно, угловая частота w равна w = (k/m)1/2 Амплитуда колебаний A и фаза колебаний j зависят от начальных условий (в момент времени t=0): начального смещение грузика x0 и начальной скорости v0. В состоянии равновесия пружина растянута на величину mg/k. Вопрос 22 Энергия гармонических колебаний Кинетическая энергия тела, совершающего гармонические колебания: Потенциальная энергия тела, совершающего гармонические колебания (под действием квазиупругой силы): Учитывая, что можно записать: Полная энергия гармонических колебаний равна сумме кинетической энергии и потенциальной энергии: При свободных колебаниях колебательная система получает энергию только в начальный момент времени, а далее энергия системы, а с ней и амплитуда колебаний не меняются. При движении тела кинетическая и потенциальная энергия переходят друг в друга. Когда отклонение системы от положения равновесия максимально, потенциальная энергия максимальна, а кинетическая равна нулю. При прохождении положения равновесия потенциальная энергия достигает минимума, а кинетическая энергия (а с ней и скорость, импульс тела) максимальна. Вопрос 23 Представление гармонического колебания с помощью векторной диаграммы
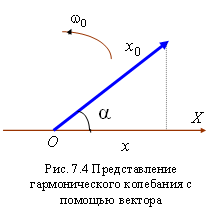 ыберем ось . Из точки О, взятой на этой оси, отложим вектор длины , образующий с осью угол . Если привести этот вектор во вращение с угловой скоростью , то проекция конца вектора на ось будет меняться со временем по закону . Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени. ыберем ось . Из точки О, взятой на этой оси, отложим вектор длины , образующий с осью угол . Если привести этот вектор во вращение с угловой скоростью , то проекция конца вектора на ось будет меняться со временем по закону . Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени.Сложение гармонических колебаний одного направления Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты, которые имеют следующий вид:
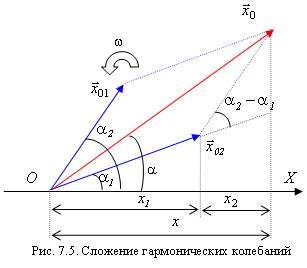 . .Представим оба колебания с помощью векторов и (рис. 7.5). Построим по правилу сложения векторов результирующий вектор . Легко увидеть, что проекция этого вектора на ось равна сумме проекций слагаемых векторов . Следовательно, вектор представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью , что и векторы , , так что результирующее движение будет гармоническим колебанием с частотой , амплитудой и начальной фазой . По теореме косинусов квадрат амплитуды результирующего колебания будет равен
Из рис. 7.5 видно, что начальная фаза результирующего колебания будет равна
Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения векторов. Формулы (7.3) и (7.4) можно, конечно, получить, сложив выражения для и аналитически, но метод векторной диаграммы отличается большей простотой и наглядностью. Вопрос 24 Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начальная фаза первого колебания равна нулю где α — разность фаз обоих колебаний, А и В -амплитуды складываемых колебаний. Исключаем из формул t. Запишем складываемые колебания как Примеры: 1) α = mπ (m=0, ±1, ±2, ...). В этом случае эллипс становится отрезком прямой 2) α = (2m+1)(π/2) (m=0, ± 1, ±2,...). В этом случае уравнение станет иметь вид 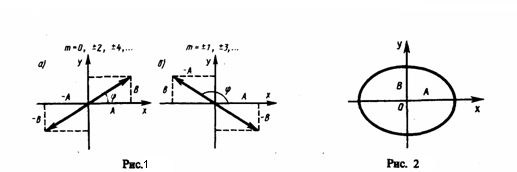 Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. 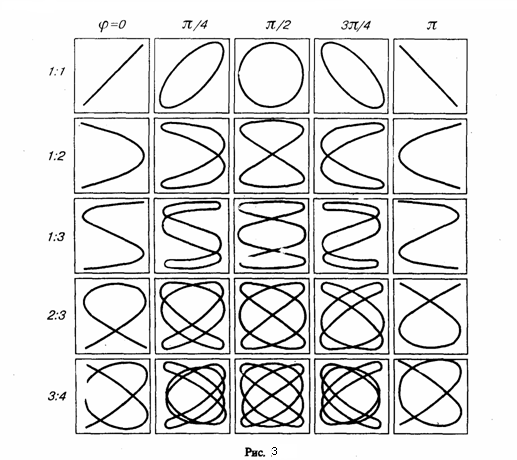 Вопрос 25 Затухающие колебания - колебания с постоянно убывающей со временем амплитудой. (из-за потерь энергии в реальной колебательной системе). Сила сопротивления где β - коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний. При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать. x''+βx’+ω02x=0 - дифференциальное уравнение затухающих колебаний. Коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D, который равен отношению амплитуд, отстоящих по времени на период Логарифмический декремент затухания равен логарифму D: 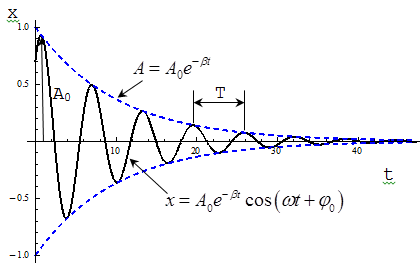 Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз.Е Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления. Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим. При приближении коэффициента затухания к W0 период колебаний становится = +∞ и колебания становятся апериодическими. Выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний, запас энергии тела к моменту его возвращения полностью расходуется на преодоление трения. При приближении коэффициента затухания к собственной частоте W0 период колебаний становится = +∞ и колебания становятся апериодическими. Вопрос 26 Если колебательная система подвергается воздействию внешней периодически изменяющейся силы, то возникают вынужденные колебания, имеющие незатухающий характер. Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющего по гармоническому закону. Для механических колебаний это внешняя вынуждающая сила F=F0 cos wt. С учетом этого закон движения для пружинного маятника запишется в виде: Далее через дифференциалы получаем: X’’+2Bx’-1W02x=f0coswt - уравнение вынужденных колебаний, где f0=F0/m – амплитуда внешнего воздействия. Если частота внешней силы приближается к собственной частоте, возникает резкое возрастание амплитуды колебаний. Это явление называется резонансом. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы называется резонансной кривой. Резонансная частота подразумевает под собой максимальные колебания, какой либо механической системы, при определенных условиях .  , где B= r/2m , где B= r/2mВопрос 27 Описание поведения реальной жидкости достаточно сложно, поэтому воспользуемся моделью несжимаемой жидкости, лишенной внутреннего трения. Такая жидкость называется идеальной. Поведение жидкости будем описывать с помощью поля скоростей. Сопоставив каждой точке жидкости характерное для нее значение скорости, получим поле скоростей (см. рис. 63). Р  ис. 63 ис. 63 Линии, касательные которым во всех точках совпадают с направлением скорости жидкости в этих точках, называются линиями тока (рис. 64). Линии, касательные которым во всех точках совпадают с направлением скорости жидкости в этих точках, называются линиями тока (рис. 64). Рис. 64 При установившемся стационарном течении жидкости линии тока не меняются со временем. Линии тока не могут пересекаться между собой. В этом случае линии тока совпадают с траекториями отдельных элементов жидкости. Такое движение называется ламинарным. При малых скоростях мы наблюдаем ламинарное течение: отдельные слои жидкости скользят друг относительно друга не перемешиваясь.С увеличением скорости характер течения жидкости меняется. Вместо слоистого течения возникают завихрения. Такое течение жидкости называется турбулентным. |

