билеты физика мифи 1 семестр. Принцип относительности Галилея. Преобразования Галилея
 Скачать 0.55 Mb.
|
|
Физика. Материя. Механическое движение. Границы применимости классической механики. Кинематика. Системы отчета. Материальная точка. Поступательное и вращательное движения абсолютно твердого тела. Радиус-вектор, перемещение, мгновенная и средняя скорости. Модуль скорости. Кинематическое описание движения материальной точки. Путь, траектория. Ускорение. Прямолинейное равнопеременное движение. Кинематические уравнения движения материальной точки. Ускорение. Ускорение в декартовой системе координат. Равноускоренное движение. Тангенциальное и нормальное ускорения (вывод). Радиус кривизны. Полное ускорение. Кинематика вращательного движения. Угловые перемещение, скорость и ускорение. Период обращения. Связь между линейными и угловыми скоростями и ускорениями. Динамика. Инерция тела. Инерциальные системы отсчета. Первый закон Ньютона. Инертность. Масса. Свойства массы. Сила. Равнодействующая сил. Динамика. Сила. Равнодействующая сил. II-й и III-й законы Ньютона и их следствия. Основное уравнение динамики материальной точки и возможные постановки задач его решения. Принцип относительности Галилея. Преобразования Галилея. Сила тяжести и вес. Сила трения. Сухое трение. Коэффициент трения. Импульс материальной точки, импульс системы материальных точек. Замкнутая система материальных точек. Вывод закона сохранения импульса. Работа. Графическая интерпретация работы. Работа постоянной, упругой и гравитационной сил. Вывод кинетической энергии частицы. Мощность. Потенциальное поле сил. Стационарное потенциальное поле. Силы консервативные и неконсервативные. Свойства консервативных сил. Потенциальная энергия частицы в поле. Связь между потенциальной энергией и силой. Полная механическая энергия частицы. Закон сохранения механической энергии частицы. Кинетическая и потенциальная энергии системы. Собственная потенциальная энергия системы частиц. Классификация сил. силы. Преобразования Лоренца. Сложение скоростей. Длина стержней и длительность событий в разных системах отчета. Основное уравнение движения в классической и релятивистской механике. Кинетическая энергии релятивистской частицы. Релятивистские выражения для массы и импульса. Масса покоя. Закон взаимосвязи массы и энергии. Энергия покоя частицы. Связь между энергией и импульсом частицы. Колебательное движение. Виды колебания (свободные, вынужденные, автоколебания, параметрические). Гармонические колебания. Уравнение гармонических колебаний и его решение. Пружинный маятник. Амплитуда, частота и фаза колебаний. Период колебаний. Энергия гармонического колебания. Кинетическая и потенциальная энергии гармонических колебаний. Представление гармонического колебания с помощью векторной диаграммы. Сложение гармонических колебаний одного направления. Сложение взаимно перпендикулярных гармонических колебаний. Фигуры Лиссажу. Уравнение затухающих колебаний. Коэффициент затухания. Период затухающих колебаний. Логарифмический декремент затухания. Добротность. Апериодические колебания. Уравнение вынужденных колебаний. Резонанс. Резонансная частота. Резонансные кривые. Идеальная жидкость. Линия тока. Трубка тока. Ламинарное течение. Описание движения жидкостей. Теорема о неразрывности струи. Вывод уравнения Бернулли. Истечение жидкости из отверстия. Число Рейнольдса. Неинерционные системы отсчета. Силы инерции. Вопрос 1 Физика - Наука, изучающая общие свойства материального мира, свойства и строение материи, формы ее движения и изменения. Материя - физическое понятие, связанное с любыми объектами, существующими в природе, о которых можно судить благодаря ощущениям. Физика описывает материю как нечто, существующее в пространстве и во времени; либо как нечто, само задающее свойства пространства и времени. Изменения во времени, происходящие с различными формами материи, составляют физические явления. Основной задачей физики является описание свойств тех или иных видов материи. Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики. Раздел механики, описывающий геометрические свойства движения без учёта причин, его вызывающих, называется кинематикой. Границы применимости классической механики В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий. Другими словами, для описания свойств атомов и субатомных частиц является квантовая механика. При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике. Кинематика — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.) Система отсчёта — это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение каких-либо тел. Математическое движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями x=f1(t), y=f2(t), z=f3(t) Материальная точка (частица) — простейшая физическая модель в механике — обладающее массой тело, размерами, формой, вращением и внутренней структурой которого можно пренебречь в условиях исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки Поступательным движение называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. Вращательное движение - Движение абсолютно твердого тела, при котором две его точки А и B остаются неподвижными, называется вращением (вращательным движением) вокруг неподвижной прямой АВ, называемой осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости - перпендикулярны к ней. Тело, вращающееся вокруг неподвижной оси, обладает одной степенью свободы: его положение полностью определяется заданием угла f поворота из некоторого начального положения. Вопрос 2 Радиус-вектор - вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат. Перемещение - вектор, соединяющий начальную и конечную точки траектории. Средняя скорость – это физическая величина, равная отношению вектора перемещения  точки к промежутку времени Δt, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения . Средняя скорость определяется по формуле: Мгновенная скорость (скорость в данный момент времени) –физическая величина, равная пределу к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:  Модуль вектора скорости равен отношению приращения длины пути к соответствующему промежутку времени:  (длина вектора).Кинематическое описание движения материальной точки. Материальной точкой называется тело, размерами и формой которого можно пренебречь в данной задаче. В декартовой системе координат положение материальной точки A в определенный момент времени, задается тремя координатами X,Y,Z или радиус-вектором , проведенным из начала координат O в данную точку A. При движении точки ее координаты изменяются с течением времени. Кинематические уравнения движения материальной точки можно записать в скалярном виде: x=x(t), y=y(t), z=z(t) или в векторной форме: Траектория – это линия, вдоль которой движется тело. Путь– скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Вопрос 3 Ускорение – векторная физическая величина, характеризующая быстроту изменения скорости. Равномерное прямолинейное движение − это движение с постоянной по модулю и направлению скоростью, при котором материальная точка совершает равные перемещения за равные промежутки времени. При прямолинейном движении траектория является прямой линией. Если направить ось X вдоль траектории, то проекции перемещения и скорости на оси Y, Z равны нулю и зависимости координаты х и модуля перемещения (в данном случае − пути) от времени для этого типа движения имеют вид: x = x0 + vхt = x0 + vt Равноускоренное прямолинейное движение — это такое движение, при котором скорость тела за равные промежутки времени изменяется одинаково, другими словами, это движение с постоянным ускорением. Ускорение a=const (по модулю и по направлению). Скорость тела меняется по закону v=v0+at Закон движения в случае равноускоренного движения имеет вид:   При движении т.М ее координаты и меняются со временем, поэтому для задания закона движения необходимо указать вид функциональной зависимости от времени всех трех её координат: ; ; , либо зависимость радиуса-вектора ;.Эти уравнения называются кинетическими уравнениями движения точки Вопрос 4 Ускорение в декартовой системе координат:  , проекции и ускорения на оси декартовой системы координат будут  , составляющие ускорения, параллельные осям координат, определятся как  , а численное значение ускорения будет равно:  . Проекцию ускорения на ось, совпадающую по направлению с вектором скорости. для определения характера движения точки (т.е. ускоренно или замедленно она движется) можно в данном случае найти, в виде: .Равноускоренное движение - движение с постоянным ускорением (a = const); движение, при котором за равные промежутки времени скорость меняется одинаково (по величине и направлению). Полное, тангенциальное и нормальное ускорения. При криволинейном движении полное ускорение материальной точки раскладывается на две составляющих: нормальное ускорение и тангенциальное ускорение :  ,  ., а – полное ускорение. Тангенциальное ускорение - ускорение, направленное параллельно мгновенной скорости и изменяющее ее по величине  .Величина тангенциального ускорения связана с величиной углового ускорения соотношением: , где — радиус траектории. Нормальное ускорение (центростремительное ускорение) — ускорение, направленное перпендикулярно мгновенной скорости и изменяющее ее по направлению . R – радиус кривизны. Радиус кривизны — величина, обратная кривизне. Радиус кривизны характеризует величину соответствия кривой от прямой. Чем больше радиус кривизны, тем больше кривая похожа на прямую. Радиус кривизны определяется для конкретной точки конкретной кривой он равняется радиусу соприкасающейся окружности. 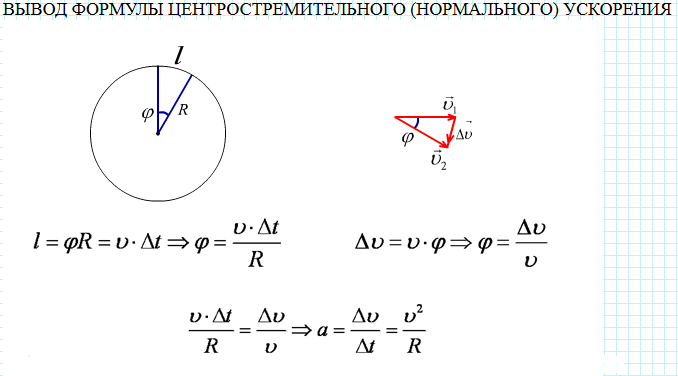 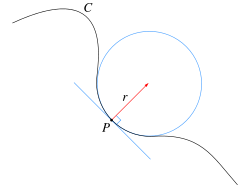 Вопрос 5 Вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси. Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:  Единица измерения угловой скорости радиан в секунду (рад/с). Таким образом, вектор ω определяет направление и быстроту вращения. Если ω=const, то вращение называется равномерным. При равномерном вращении его можно охарактеризовать периодом вращения Т –временем, за которое точка тела совершает один полный оборот, т.е. поворачивается на угол 2π:  Число полных оборотов, совершаемых телом при равномерном движении по окружности, в единицу времени называется частотой вращения:  О  ткуда Связь между линейной и угловой скоростями. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь  . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так: Так как  , то Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:  Следовательно,  Вопрос 6 Динамика — раздел механики, в котором изучаются причины возникновения механического движения. Инерция — свойство тел оставаться в некоторых системах отсчёта в состоянии покоя или равномерного прямолинейного движения в отсутствии или при взаимной компенсации внешних воздействий. Инерциальная система отсчёта — система отсчёта, в которой все свободные тела движутся прямолинейно (вдоль одной прямой) и равномерно (с постоянной скоростью). Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения. |