билеты физика мифи 1 семестр. Принцип относительности Галилея. Преобразования Галилея
 Скачать 0.55 Mb.
|
Часть жидкости, ограниченная линиями тока, называется трубкой тока (рис. 65).  При стационарном течении жидкости ее количество, протекающее в единицу времени через сечение S1, равно количеству жидкости, протекающему в единицу времени через другое сечение S2, если плотность жидкости постоянна (рис.66). 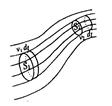 Масса жидкости, протекающей через некоторое сечение за время dt равна:  .Тогда из вышесказанного следует, что:  . Т.к. плотность постоянна, то это условие принимает вид:  .(в лекции вместо плотности использована скорость) Это соотношение называют уравнением неразрывности струи. Вопрос 28 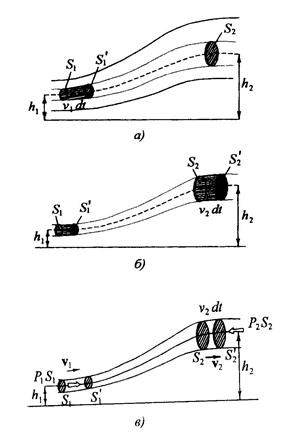 Рассмотрим часть жидкости, заключенной между сечениями S1 и S2 выделенной трубки тока, расположенными на высотах h1 и h2 (рис. 65). За промежуток времени dt эта часть жидкости смещается вдоль трубки тока и занимает положение между сечениями и . Работа внешних сил, действующих на выделенный элемент жидкости, запишем в следующем виде:  . Это связано с тем, что силы давления, действующие на боковую поверхность трубки тока, перпендикулярны перемещению жидкости и работы не совершают, а работы сил давления в сечениях и отличаются знаком. Тогда можем получить: ,  здесь dm – масса жидкости между указанными сечениями.Изменение энергии рассматриваемой части жидкости равно энергии части жидкости между сечениями и минус энергия части жидкости между сечениями и . Кинетическая энергия части жидкости между сечениями и определится как:  .Потенциальная энергия определится как:  .Аналогично записывается энергия, заключенная между сечениями и . В результате изменение энергии всей выделенной массы жидкости за время dt равно: .  Работа внешних сил равна изменению механической энергии системы:. Это уравнение 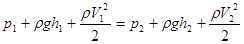 называется уравнением Бернулли. Для каждого вида течения существует критическое число Рейнольдса, Re крR e κ ρ , которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При Re< Re кр R e < R e κ ρ течение происходит в ламинарном режиме, при Re > Re кр R e > R e κ ρ возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, такими как изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др. Истечение жидкости из отверстия. Выделим в жидкости трубку тока, имеющую своим сечением с одной стороны открытую поверхность жидкости в сосуде, а с другой стороны — отверстие, через которое жидкость вытекает. Уравнение Бернули в данном случае будет иметь вид:  где v — скорость истечения из отверстия. Сократив на ρ и введя h=h1-h2 — высоту открытой поверхности жидкости над отверстием, получим: ϑ2/2=gh, откуда  Эта формула называется формулой Торричелли.Итак, скорость истечения жидкости из отверстия, расположенного на глубине h под открытой поверхностью, совпадает со скоростью, которую приобретает любое тело, падая с высоты h (жидкость идеальна). Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличается от значения ф.Торричелли, чем больше вязкость жидкости. 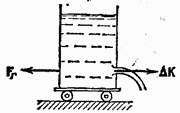 Струя жидкости, вытекающая из отверстия в сосуде, уносит с собой за время Δt импульс ΔK=ρSϑVΔt (ρ — плотность жидкости, S — площадь отверстия, v — скорость истечения струи). Этот импульс сообщается вытекающей жидкости сосудом. По третьему закону Ньютона сосуд получает от вытекающей жидкости за время Δt импульс, равный -ΔK, т. е. испытывает действие силы  Эта сила называется реакцией вытекающей струи. Если сосуд поставить на тележку, то под действием силы F, он придет в движение в направлении, противоположном направлению струи. Найдем значение силы Fr воспользовавшись выражением для скорости истечения жидкости из отверстия:  Возникающее при вытекании струи движение жидкости в сосуде приводит к перераспределению давления, причем давление вблизи стенки, лежащей против отверстия, оказывается несколько большим, чем вблизи стенки, в которой сделано отверстие. Вопрос 29 Инерциальные системы – которые движутся вдоль одной прямой с постоянной скоростью. Системы отсчета, которые движутся относительно инерциальной системы с ускорением, называются неинерциальными. В них законы Ньютона не применяются. Однако законы динамики можно применять и для них, если кроме сил, которые обусловлены воздействием тел друг на друга, ввести в рассмотрение понятие силы особого рода - так называемую силу инерции. При учете сил инерции второй закон Ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (учитывая и силы инерции). При этом силы инерции Fin должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение а', каким оно обладает в неинерциальных системах отсчета, т. е.  Так как F=ma (a - ускорение тела в инерциальной системе отсчета), то  Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы. Пример: силы инерции при ускоренном поступательном движении системы отсчета; На тележке к штативу на нити подвешен шарик массой m. Пока тележка покоится или движется прямолинейно и равномерно, нить, которая удерживает шарик, занимает вертикальное положение, и сила тяжести Р уравновешивается силой реакции (натяжения) нити Т. 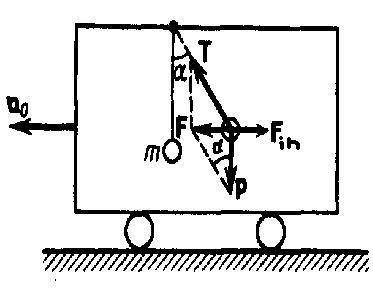 Если тележку привести в поступательное движение с ускорением а0, то нить будет отклоняться от вертикали в сторону, обратную движению, до такого угла α, пока результирующая сила F=P+T не даст ускорение шарика, равное а0. Значит, результирующая сила F направлена в сторону ускорения тележки а0 и для установившегося движения шарика (теперь шарик движется вместе с тележкой с ускорением а0) равна F=mgtgα=ma0, откуда  т. е. угол отклонения нити от вертикали тем больше, чем больше ускорение тележки. В системе отсчета, которая связана с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой Fin, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Таким образом,  (2)Силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Если на тело действует сила инерции, то не существует силы, противодействующей ей и приложенной к данному телу. Для любого из тел, которые находятся в неинерциальной системе отсчета, силы инерции являются внешними; Значит, здесь нет замкнутых систем, т.е. в неинерциальных системах отсчета не выполняются также и законы сохранения импульса, энергии и момента импульса. Значит, силы инерции действуют только в неинерциальных системах отсчета. В инерциальных системах отсчета таких сил не существует. Силы инерции, которые действуют на тела в неинерциальной системе отсчета, пропорциональны их массам и при прочих равных условиях сообщают этим телам одинаковые ускорения. Значит в поле сил инерции эти тела движутся абсолютно одинаково, если только одинаковы начальные условия. силы инерции, которые действуют на тело, покоящееся во вращающейся системе отсчета; 3) силы инерции, которые действуют на тело, движущееся во вращающейся системе отсчета. Относительно системы отсчета, которая связана с вращающимся диском, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой Fс, являющаяся ничем иным, как силой инерции, так как никакие другие силы на шарик не действуют. Сила Fc, называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна  (3) Чтобы заставить шарик катиться по вращающемуся диску вдоль радиуса, будем использовать жестко укрепленный вдоль радиуса диска стержень, на котором шарик движется без трения прямолинейно равномерно со скоростью ν' (рис. 3б). При отклонении шарика стержень действует на него с некоторой силой F. Во вращающейся системы отсчета, т.е. относительно диска, шарик движется прямолинейно и раномерно, что объясняется тем, что сила F уравновешивается приложенной к шарику силой инерции Fk, которая перпендикулярной скорости ν'. Эта сила называется кориолисовой силой инерции. Можно показать, что сила Кориолиса  Сила Кориолиса действует только на тела, которые движутся относительно вращающейся системы отсчета. |