лабораторки MPI. Принципы работы mpi в операционной системе Windows Краткая теория
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
Создание MPI-программы в Visual StudioПрежде всего, нужно настроим Visual Studio, чтобы он находил заголовочные файлы и .lib-библиотеки MPICH. Для этого запускаем Visual Studio и Tools → Options, в дереве слева выбераем Projects and Solutions → VC++ Directories. Справа-вверху выберем Show directories for: Include files. Путь к .h-файлам (рис. 2.1.) 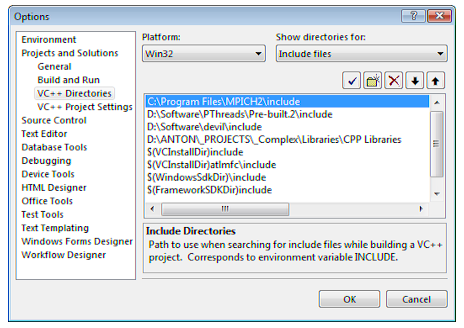 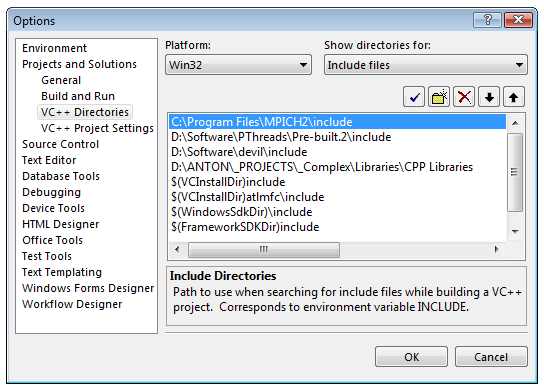 Рис 2.1. Настройка пути к заголовочным файлам MPICH После этого проделаем ту же процедуру для библиотек (Show directories for: Library files) (Рис. 2.2.): 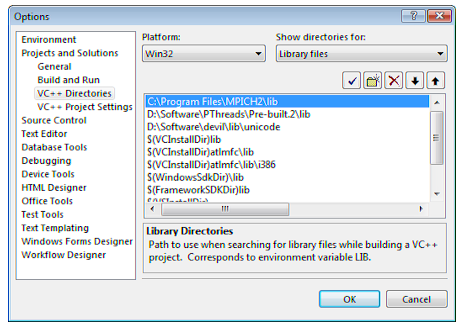 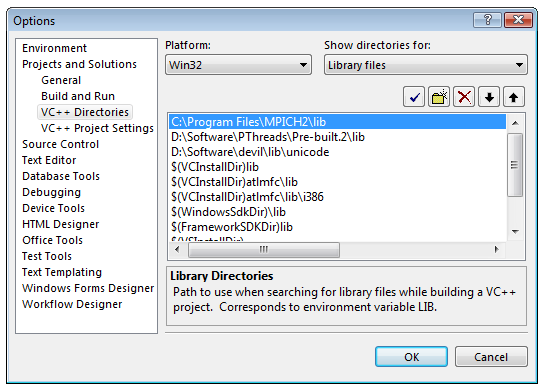 Рис 2.2. Настройка пути к библиотечным файлам MPICH Теперь создаем консольный проект. Откроем окно настроек проекта (Project → Properties), выберем Configuration: All Configurations, в дереве слева выберите Configuration Properties → Linker → Input. Добавим mpi.lib в поле Additional Dependencies справа (Рис. 2.3.): 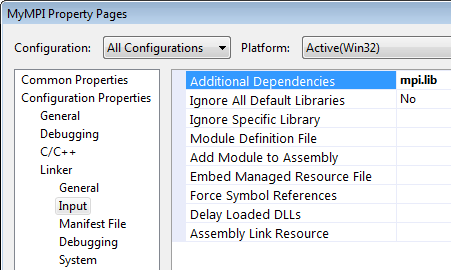 Рис 2.3. Добавление mpi.lib к программе Исходный код примера 2.1 /* This is an interactive version of cpi */ #include "mpi.h" #include #include #include double f(double); int main(int argc, char **argv) { int done = 0, n, myid, numprocs, i; double PI25DT = 3.141592653589793238462643; double mypi, pi, h, sum, x; double startwtime = 0.0, endwtime; int namelen; char processor_name[MPI_MAX_PROCESSOR_NAME]; MPI_Init(&argc,&argv); MPI_Comm_size(MPI_COMM_WORLD,&numprocs); MPI_Comm_rank(MPI_COMM_WORLD,&myid); MPI_Get_processor_name(processor_name,&namelen); /* fprintf(stdout,"Process %d of %d is on %s\n", myid, numprocs, processor_name); fflush(stdout); */ while (!done) { if (myid == 0) { fprintf(stdout, "Enter the number of intervals: (0 quits) "); fflush(stdout); if (scanf("%d",&n) != 1) { fprintf( stdout, "No number entered; quitting\n" ); n = 0; } startwtime = MPI_Wtime(); } MPI_Bcast(&n, 1, MPI_INT, 0, MPI_COMM_WORLD); if (n == 0) done = 1; else { h = 1.0 / (double) n; sum = 0.0; for (i = myid + 1; i <= n; i += numprocs) { x = h * ((double)i - 0.5); sum += f(x); } mypi = h * sum; MPI_Reduce(&mypi, &pi, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD); if (myid == 0) { printf("pi is approximately %.16f, Error is %.16f\n", pi, fabs(pi - PI25DT)); endwtime = MPI_Wtime(); printf("wall clock time = %f\n", endwtime-startwtime); fflush( stdout ); } } } MPI_Finalize(); _getch(); return(0); } double f(double a) { return (4.0 / (1.0 + a*a)); } Методы распараллеливания и модели программ, поддерживаемые MPI Одной из целей, преследуемых при решении задач на вычислительных системах, в том числе и на параллельных, – является эффективность. Эффективность параллельной программы существенно зависит от соотношения времени вычислений ко времени коммуникаций между компьютерами (при обмене данными). И чем меньше в процентном отношении доля времени, затраченного на коммуникации, в общем времени вычислений, тем больше эффективность. Для параллельных систем с передачей сообщений оптимальное соотношение между вычислениями и коммуникациями обеспечивают методы крупнозернистого распараллеливания, когда параллельные алгоритмы строятся из крупных и редко взаимодействующих блоков. Задачи линейной алгебры, задачи, решаемые сеточными методами и многие другие, достаточно эффективно распараллеливаются крупнозернистыми методами. MPMD - модель вычислений. MPI - программа представляет собой совокупность автономных процессов, функционирующих под управлением своих собственных программ и взаимодействующих посредством стандартного набора библиотечных процедур для передачи и приема сообщений. Таким образом, в самом общем случае MPI - программа реализует MPMD - модель программирования (Multiple program - Multiple Data). SPMD - модель вычислений. Все процессы исполняют в общем случае различные ветви одной и той же программы. Такой подход обусловлен тем обстоятельством, что задача может быть достаточно естественным образом разбита на подзадачи, решаемые по одному алгоритму. На практике чаще всего встречается именно эта модель программирования (Single program - Multiple Data). Последнюю модель иначе можно назвать моделью распараллеливания по данным. Кратко, суть этого способа заключается в следующем. Исходные данные задачи распределяются по процессам (ветвям параллельного алгоритма), а алгоритм является одним и тем же во всех процессах, но действия этого алгоритма распределяются в соответствии с имеющимися в этих процессах данными. Распределение действий алгоритма заключается, например, в присвоении разных значений переменным одних и тех же циклов в разных ветвях, либо в исполнении в разных ветвях разного количества витков одних и тех же циклов и т.п. Другими словами, процесс в каждой ветви следует различными путями выполнения на той же самой программе. Виртуальные топологии В этом пункте описываем механизм виртуальных топологий MPI. Под виртуальной топологией здесь понимается программно реализуемая топология в виде конкретного графа, например: кольцо, решетка, тор, звезда, дерево и вообще произвольно задаваемый граф на существующей физической топологии. Виртуальная топология обеспечивает очень удобный механизм наименования процессов, связанных коммуникатором, и является мощным средством отображения процессов на оборудование системы. Виртуальная топология в MPI может задаваться только в группе процессов, объединенных коммуникатором. Нужно различать виртуальную топологию процессов и топологию основного, физического оборудования. Механизм виртуальных топологий значительно упрощает и облегчает написание параллельных программ, делает программы легко читаемыми и понятными. Пользователю при этом не нужно программировать схему физических связей процессоров, а только программировать схему виртуальных связей между процессами. Отображение виртуальных связей на физические связи осуществляет система, что делает параллельные программы машинно-независимыми и легко переносимыми. Функции в этой главе осуществляют только машинно-независимое отображение. Функции создания декартовых топологий Функция, конструирующая декартову топологию MPI_CART_CREATE используется для описания декартовой структуры произвольного измерения. Для каждого направления координаты определяется, является ли структура процесса периодической или нет. MPI_CART_CREATE(comm_old, ndims, dims, periods, reorder, comm_cart) IN comm_old входной (старый) коммуникатор IN ndims количество измерений в декартовой топологии IN dims целочисленный массив размером ndims, определяющий количество процессов в каждом измерении IN periods массив размером ndims логических значений,определяющих переодичность (true) или нет (false) в каждом измерении IN reorder ранги могут быть перуномерованы (true) или нет (false) OUT comm_cart коммуникатор новой (созданой) декартовой топологии int MPI_Cart_create(MPI_Comm comm_old, int ndims, int *dims, int *periods, int reorder, MPI Comm *comm_cart) MPI_CART_CREATE возвращает управление новому коммуникатору, к которому присоединена информация декартовой топологии. Эта функция коллективная. Как в случае с другими коллективными функциями, вызов этой функции должен быть синхронизован во всех процессах. Если reorder = false, тогда номер каждого процесса в новой группе идентичен ее номеру в старой группе. Иначе, функция может переупорядочивать процессы (возможно чтобы выбрать хорошее отображение виртуальной топологии на физическую топологию). Если полный размер декартовой сетки меньше чем размер группы comm_old, то некоторые процессы возвращают MPI_COMM_NULL, по аналогии с MPI_COMM_SPLIT. Запрос ошибочен, если он определяет сетку, которая является большей, чем размер группы comm_old (Рис. 3.1).
Рис. 3.1. Связь между рангами и декартовыми координатами для 3x4 2D топологии. Верхний номер в каждой клетке - номер процесса, а нижнее значение (строка, столбец) - координаты. Декартова функция задания решетки Для декартовой топологии, функция MPI_DIMS_CREATE помогает пользователю выбрать сбалансированное распределение процессов по направлению координат, в зависимости от числа процессов в группе, и необязательных ограничений, которые могут быть определены пользователем. Одно возможное использование этой функции это разбиение всех процессов (размер группы MPI_COMM_WORLD) в N-мерную топологию. MPI_DIMS_CREATE(nnodes, ndims, dims) IN nnodes количество узлов в решетке IN ndims размерность декартовой топологии INOUT dims целочисленный массив, определяющий количество узлов в каждой размерности int MPI_Dims_create(int nnodes, int ndims, int *dims) Элементы в массиве dims представляют описание декартовой решетки с размерностями ndims и общим количеством узлов nnodes. Размерности устанавливаются так, чтобы быть близко друг к другу насколько возможно, используя соответствующий алгоритм делимости. Пользователь может ограничивать действие этой функции, определяя элементы массива dims. Если в dims[i] уже записано число, то функция не будет изменять количество узлов в измерении i; функция модифицирует только нулевые элементы в массиве, т.е. где dims[i] = 0. Отрицательные значения элементов dims(i) ошибочены. Ошибка будет выдаваться, если nnodes не кратно П dims[i]. (i,dims[i]¹0) Для dims[i] установленных функцией, dims[i] будут упорядочены в монотонно уменьшающемся порядке. Массив dims подходит для использования, как вход к функции MPI_CART_CREATE. Функция MPI_DIMS_CREATE локальная. Отдельные типовые запросы показываются на Рис 3.2.
Рис. 3.2. Отдельные типовые запросы к функции MPI_DIMS_CREATE. Декартовы информационные функции Если декартова топология создана, может возникнуть необходимость запросить информацию относительно этой топологии. Эти функции даются ниже и все они локальные. MPI_CARTDIM_GET(comm, ndims) IN comm коммуникатор с декартовой топологией OUT ndims размерность декартовой топологии int MPI_Cartdim_get(MPI_Comm comm, int *ndims) MPI_CARTDIM_GET возвращает число измерений декартовой топологии, связанной с коммуникатором comm. Коммуникатор с топологией на рис. 1.2 возвратил бы ndims = 2. MPI_CART_GET(comm, maxdims, dims, periods, coords) IN comm коммуникатор с декартовой топологией IN maxdims максимальный размер массивов dims, periods, и coords в вызывающей программе OUT dims массив значений, указывающих количество процессов в каждом измерении OUT periods массив значений, указывающих периодичность (true/false) в каждом измерении OUT coords координаты вызвавшего процесса в декартовой топологии int MPI_Cart_get(MPI_Comm comm, int maxdims, int *dims, int *periods, int *coords) MPI_CART_GET возвращает информацию относительно декартовой топологии, связанной с коммуникатором comm. maxdims должен быть, по крайней мере, равен ndims, как возвращает MPI_CARTDIM_GET. Для примера на рис. 1.2, dims = (3,4), а в процессе 6 функция возвратит coords = (1,2). Декартовы функции транслирования Функции, приведенные в этом пункте переводят на\из ранга в декартовы координаты топологии. Эти запросы локальные. MPI_CART_RANK(comm, coords, rank) IN comm коммуникатор с декартовой топологией IN coords целочисленный массив, определяющий координаты нужного процесса в декартовой топологии OUT rank ранг нужного процесса int MPI_Cart_rank(MPI_Comm comm, int *coords, int *rank) Для группы процессов с декартовой структурой функция MPI_CART_RANK переводит логические координаты процессов в номера. Эти номера процессы используют в парных взаимодействиях между процессами. coords - массив размером ndims как возвращает MPI_CARTDIM_GET. Для примера на рис. 1.2 процесс с coords = (1,2) возвратил бы rank = 6. Для измерения i с periods(i) = true, если координата, coords(i), находится вне диапазона, то есть coords(i) < 0 или coords(i) >= dims(i), она перемещается назад к интервалу 0 <= coords(i) < dims(i) автоматически. Если топология на рис. 1.2 периодическая в обеих размерностях, то процесс с coords = (4,6) также возвратил бы rank = 6. Для непериодических размерностей диапазон вне координат ошибочен. MPI_CART_COORDS(comm, rank, maxdims, coords) IN comm коммуникатор с декартовой топологией IN rank ранг процесса в торологии comm IN maxdims максимальный размер массивов dims, periods, и coords в вызывающей программе OUT coords целочисленный массив, определяющий координаты нужного процесса в декартовой топологии int MPI_Cart_coords(MPI_Comm comm, int rank, int maxdims, int *coords) MPI_CART_COORDS – переводит номер процесса в координаты процесса в топологии. Это обратное отображение MPI_CART_RANK. maxdims можно взять, например, равным ndims, возвращенным MPI_CARTDIM_GET. Для примера на рис. 1.2, процесс с rank = 6 возвратил бы coords = (1,2). Декартова функция смещения Если в декартовой топологии, используется функция MPI_SENDRECV (см. далее п. 3.2) для смещения данных вдоль направления какой либо координаты, то входным аргументом MPI_SENDRECV берется номер процесса source (процесса источника) для приема данных, и номер процесса dest (процесса назначения) для передачи данных. Операция смещения в декартовой топологии определяется координатой смещения и размером шага смещения (положительным или отрицательным). Функция MPI_CART_SHIFT возвращает информацию для входных спецификаций, требуемых в вызове MPI_SENDRECV. Функция MPI_CART_SHIFT локальная. MPI_CART_SHIFT(comm, direction, disp, rank_source, rank_dest) IN comm коммуникатор с декартовой топологией IN direction номер измерения (в топологии), где делается смещение IN disp направление смещения (> 0: смещение в сторону увеличения номеров координаты direction, < 0: смещение в сторону уменьшения номеров координаты direction) OUT rank_source ранг процесса источника OUT rank_dest ранг процесса назначения int MPI_Cart_shift(MPI_Comm comm, int direction, int disp, int *rank_source, int *rank_dest) Аргумент direction указывает измерение, в котором осуществляется смещение данных. Измерения маркируются от 0 до ndims-1, где ndims - число размерностей. disp указывает направление и величину смещения. Например, в топологии "линейка" или "кольцо" с N ≥ 4 процессами для процесса с номером 1 при disp = +1 rank_source = 0, а rank_dest = 2; при disp = -1 rank_source = 2, а rank_dest = 0. Для этого же процесса 1 при disp = +2 rank_source = N-1 для "кольца" и MPI_PROC_NULL для "линейки", а rank_dest = 3 для обоих структур; при disp = -2 rank_source = 3 для обоих структур, а rank_dest = N-1 для "кольца" и MPI_PROC_NULL для "линейки". В зависимости от периодичности декартовой топологии в указанном направлении координат, MPI_CART_SHIFT обеспечивает идентификаторы rank_source и rank_dest для кольцевого или не кольцевого смещения данных. Это имеющие силу входные аргументы к функции MPI_SENDRECV. Ни MPI_CART_SHIFT, ни MPI_SENDRECV не коллективные функции. Не требуется, чтобы все процессы в декартовой решетке одновременно вызвали MPI_CART_SHIFT с теми же самыми direction и disp аргументами, но только тот процесс, который посылает соответственно, получает в последующих запросах к MPI_SENDRECV. |
