БУрение скважин с применением технологии колтюбинга. КОЛТЮБИНГ. Проблемы, которым посвящена эта работа, в равной степени относятся и к бурению, и к подземному ремонту, и к исследованию скважин
 Скачать 397.13 Kb. Скачать 397.13 Kb.
|
|
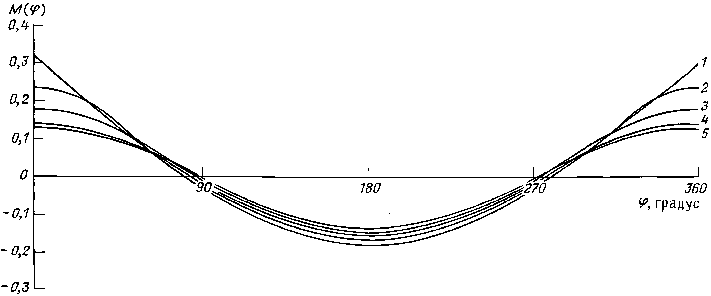
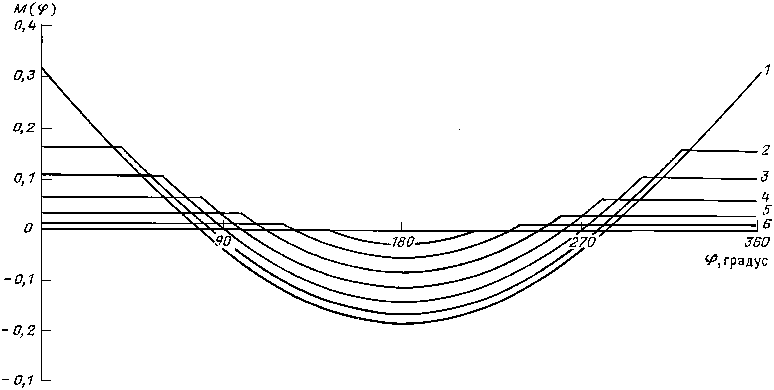
3.ОСНОВНЫЕ УЗЛЫ АГРЕГАТОВ, ИХ РАСЧЕТ И КОНСТРУИРОВАНИЕ 3.1. ТРАНСПОРТЕР КОЛОННЫ ГИБКИХ ТРУБ (ИНЖЕКТОР) Кинематический расчет Цель расчетов, приведенных в данном разделе, заключается в определении взаимосвязи скорости перемещения колонны гибких труб и подачи рабочей жидкости гидропривода к гидромоторам транспортера. Два гидромотора, приводящие в действие цепи транспортера, получают рабочую жидкость от насоса того же типа, что и каждый гидромотор. Подача насоса Qф = qкnфK0/1000, где qк – объем рабочей камеры насоса (qк = 112 см3); nф – фактическая частота вращения вала гидромотора; коэффициента подачи насоса K0 = 0,95. При nф = 1500 об/мин Qф = 11215000,95/1000 = 159,6 л/мин. Угловая скорость вращения вала гидромотора г = [(Qф/2)Kом1000]/30qк, где Kом – объемный КПД гидромотора (Kом = 0,95). Соответственно угловая скорость вращения звездочки инжекторного механизма г = [(Qф/2)Kом1000]/30iqк, где i – передаточное отношение редуктора транспортера. Скорость подъема непрерывной трубы v = гR, где R – радиус звездочки, которая приводит в действие цепь инжекторного механизма (R = 114 мм). В результате v = [R(Qф/2)Kом1000]/30iqк. Скорость перемещения трубы при номинальной частоте вращения вала приводного двигателя v = [0,114(159,6/2)3,140,951000]/3024112 = 0,336 м/с. При работе приводного двигателя с максимальной частотой вращения nф = 1800 об/мин, подача насосов Qф = 191 л/мин и соответственно скорость перемещения трубы v = 0,4 м/с. Определение допускаемого усилия на плашки Усилие, с которым плашки воздействуют на трубу, однозначно связано с величинами напряжений, возникающих в последней. Для определения максимально допустимого значения усилий проследим взаимосвязь внутренних силовых факторов и внешней нагрузки. Для оценки напряжений, возникающих в продольных сечениях гибкой трубы, сжатой плашками, рассмотрим возможные варианты их взаимодействия, которые определяют картину приложения внешних сил к трубе. В дальнейшем примем следующие допущения, которые, как показывает практика, достаточно обоснованы: плашка представляет собой абсолютно жесткий монолит, а труба – упругое тело.При взаимодействии плашек с трубой возможны три варианта приложения сил: а) при Rтр.н < Rп возникает ситуация, изображенная на рис. 12, а; б) при Rтр.н > Rп имеет место вариант, представленный на рис. 12, в; в) при Rтр.н = Rп характерной является картина, изображенная на рис. 12, б. Здесь Rтр.н – наружный радиус гибкой трубы, Rп – радиус кривизны контактной поверхности плашек. Картины взаимодействия плашки и трубы, представленные на рис. 12, а, в, могут наблюдаться не только при несоответствии размеров трубы и плашки, но и при деформации поперечного сечения трубы. Помимо этого встречаются и другие варианты приложения нагрузки, например, несимметричный. В этом случае каждая из плашек по-своему взаимодействует с трубой. 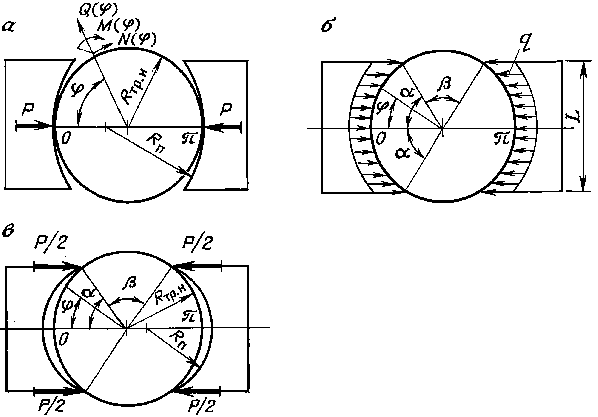 Рис. 12. Схема взаимодействия плашек транспортера с гибкой трубой: при сжатии трубы: а – двумя сосредоточенными силами, б – равномерно распределенной нагрузкой, в – двумя парами сосредоточенных сил Для определения наиболее опасного с точки зрения прочности трубы случая взаимодействия плашки с ее поверхностью рассмотрим внутренние силовые факторы (см. рис. 12), возникающие при различных вариантах приложения сил . Приложение двух сосредоточенных сил. Этот случай соответствует соотношению Rтр.н < Rп (см. рис. 12, а). При этом в поперечных сечениях трубы с угловой координатой действуют следующие силы: нормальная N() = 0,5Рsin; поперечная Q() = 0,5Рсos; изгибающий момент M() = РRтр.н(0,3183 – 0,5sin). Приложение двух пар сосредоточенных сил. Этот случай соответствует соотношению Rтр.н > Rп. Здесь также в качестве координаты рассматриваемого сечения принят угол . Нормальная сила: интервал 0 N() = –(P/2)[0,3183сos(sin2 – sin2)]; интервал N() = –(P/2)[0,3183сos(sin2 –sin2) + sin]; нтервал N() = –(P/2)[0,3183сos(sin2 – sin2)]. Поперечная сила: интервал 0 Q() = (–P/2)[0,3183sin(sin2 – sin2)]; интервал Q() = (–P/2)[0,3183sin(sin2 – sin2) + сos]; интервал Q() = (–P/2)[0,3183sin(sin2 – sin2)]. Изгибающий момент: интервал 0 M() = (PRтр.н/2)[0,3183(sin + сos – sin – сos – – sin2сos + sin2сos) – sin + sin]; интервал M() = (PRтр.н/2)[0,3183(sin + сos – sin – сos – – sin2сos + sin2сos) – sin + sin]; интервал M() = (PRтр.н/2)[0,3183(sin + сos – sin – сos – – sin2сos + sin2сos)]. В рассматриваемом случае нагружения трубы предполагают, что каждая из действующих сил равна половине усилия, приложенного к плашке. Приложение распределенной нагрузки. Этот случай соответствует соотношению Rтр.н = Rп (см. рис. 12, б). Значение характеризует текущую угловую координату продольного сечения, в которой определяется изгибающий момент, а – половину угла охвата трубы плашкой. Силовые факторы в поперечных сечениях определяются следующим образом. Нормальная сила: интервал 0 N() = –qRтр.нsin2; интервал – N() = –qRтр.нsinsin. Поперечная сила: интервал 0 Q() = qRтр.нsinсos; интервал – Q() = qRтр.нsinсos. Изгибающий момент: интервал 0 M() = qR2тр.н{(1/)[(0,5 + sin2 + 1,5sinсos)] – – 0,5 sin2 – 0,5sin2}; интервал – M() = qR2тр.н{(1/)[(0,5 + sin2) + 1,5sinсos] – – 0,5sin2 – sinsin + 0,5sin2}. Для определения экстремальных значений изгибающих моментов в безразмерной форме были построены эпюры, характеризующие зависимости M() для различных условий приложения нагрузки. Для обеспечения возможности сопоставления получаемых величин по формулам при распределенной нагрузке коэффициент выражен через величину силы P, приложенной к плашке, и ее ширину Lï = 2Rsin. Тогда qR2тр.н = R2тр.нP/L = R2тр.нP/2Rтр.нsin = PRтр.н/2sin. Отсюда величины безразмерных изгибающих моментов M1() могут быть представлены следующим образом: при приложении двух сосредоточенных сил M1() = M()/PRтр.н = –0,3183 + 0,5sin; при приложении двух пар сосредоточенных сил интервал 0 M1() = M()/2PRтр.н = (1/2)[0,3183(sin + сos – sin – – сos – sin2сos + sin2сos) – sin + sin]; интервал M1() = M()/2PRтр.н = (1/2)[0,3183(sin + сos – sin – – cos – sin2сos + sin2сos) – sin + sin; интервал M1() = M()/2PRтр.н = (1/2)[0,3183(sin + cos – sin – – сos – sin2сos) + sin2сos)]; при приложении распределенной нагрузки интервал 0 M1() = M()/(PRтр.н) = [1/(2sin)]{(1/)[(0,5 + + sin2 + 1,5sinсos] – 0,5sin2 – 0,5sin2}; интервал – M1() = M()/(PRтр.н/2sin) = [1/(2sin)]{(1/)[(0,5 + + sin2 + 1,5sinсos] – 0,5sin2 – sinsin + 0,5sin2}. Графики, иллюстрирующие изменение изгибающего момента, приведены на рис. 13, 14. Из них следует, что оптимальным с точки зрения минимизации напряжений, возникающих при сжатии плашкой трубы и действии распределенной нагрузки, является значение угла охвата , близкое к 90. Достигнуть такой величины по конструктивным соображениям невозможно, поэтому в качестве максимального значения следует принимать = 80 85. Это же положение относится и к случаю действия двух пар сосредоточенных сил. Однако этот вариант нагружения является промежуточным при переходе к распределенной нагрузке. При условии равенства геометрических размеров поперечных сечений гибких труб для трех рассмотренных вариантов взаимодействия их с плашками наиболее опасным будет случай, при котором возникает максимальный по модулю изгибающий момент. При проведении прочностных расчетов следует, в первую очередь, учитывать растягивающие напряжения, которые суммируются с растягивающими напряжениями, возникающими при действии давления технологической жидкости. Максимальные значения изгибающих моментов для трех рассмотренных случаев представлены ниже:
Из приведенных данных следует, что наиболее предпочтительным случаем при взаимодействии трубы и плашек является приложение распределенной нагрузки. Вместе с тем, при действии двух сосредоточенных сил деформация поперечного сечения трубы приводит к увеличению площади контакта и в итоге к передаче усилия по всей площади плашки. Картина деформации поперечного сечения при приложении двух пар сосредоточенных сил является более сложной. При угле 40 50 они могут вызвать сплющивание трубы. Но поскольку подобные значения углов в плашках не предусмотрены, данный вопрос как представляющий сугубо теоретический интерес рассмотрен не будет. Исходя из полученных зависимостей ,может быть вычислен изгибающий момент и определены максимальные напряжения, возникающие при обжатии трубы плашками. Рассмотрим пример расчета напряжений в предположении, что отсутствует давление технологической жидкости во внутренней полости трубы и на нее нет осевой нагрузки. Под действием изгибающего момента в продольном сечении гибкой трубы возникают нормальные напряжения, максимальное значение которых определяется следующим образом: x = Mx1/Wx1, где Mx1 = KнагрP1R – максимальное значение изгибающего момента, действующего в поперечном сечении, в расчете на единицу длины трубы (значения максимальных моментов и соответствующих коэффициентов нагружения Kнагр приведены выше); Wx1 = bтр2тр/6 – момент сопротивления изгибу поперечного сечения трубы, имеющей длину, равную единице (где тр – толщина стенки трубы; bтр – ширина ее поперечного сечения, в рассматриваемом случае b = 1). Моменты сопротивления изгибу для труб различной толщины имеют следующие значения:
|