лекция геометрические тела. Проекционное черчение. Проецирование основных геометрических фигур
 Скачать 1.16 Mb. Скачать 1.16 Mb.
|
|
Способ вращения. Способ заключается в том, что геометрическую фигуру поворачивают до нужного положения вокруг неподвижной прямой — оси вращения U. Осью вращения может быть прямая любого положения. Однако проще всего поворачивать геометрические фигуры вокруг осей, перпендикулярных плоскостям проекций. Способ вращения рассмотрим на примере поворота точки А на угол 150° вокруг оси U, перпендикулярной плоскости Н (рис.28,а).Предположим, что точку А надо вращать в направлении против движения часовой стрелки. Точка А вращается в плоскости Т, перпендикулярной оси вращения U и, следовательно, параллельной плоскости Н. При вращении точка А описывает дугу окружности радиуса RАс центром в точке О, расположенной на оси вращения U. Эта дуга и угол поворота точки А, равный 150°, проецируются без искажения на плоскость Н. На плоскость V дуга окружности радиуса RАпроецируется в виде отрезка, параллельного оси X. Положение точки А после поворота обозначают А1, а ее новые проекции — а1 и а1'. 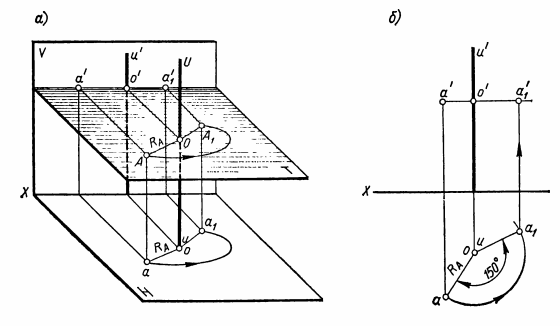 Рис.28 На проекциях (рис.28,б)изображение точки А после поворота ее вначале получают на плоскости Н. Для этого проводят дугу окружности радиуса RA = oa с центром в точке о. По дуге в заданном направлении от точки а отмеряют угол 150° и получают точку а1. На плоскость V траектория вращения точки А проецируется в виде отрезка прямой, параллельного оси X и проходящего через точку а'. Новую фронтальную проекцию а1' точки А получают на пересечении линии связи, проведенной через точку а1, с прямой, параллельной оси X и проведенной через точку а'. Поворот точки вокруг оси U⊥ V аналогичен повороту точки вокруг оси U⊥H. Наглядное представление о вращении точки В вокруг оси U, перпендикулярной плоскости V, можно получить из рис.29,а. Для примера точка В повернута на угол 60° по движению часовой стрелки. Построение проекций точки В после поворота показано на рис. 29,б. Порядок построения проекций указан стрелками. 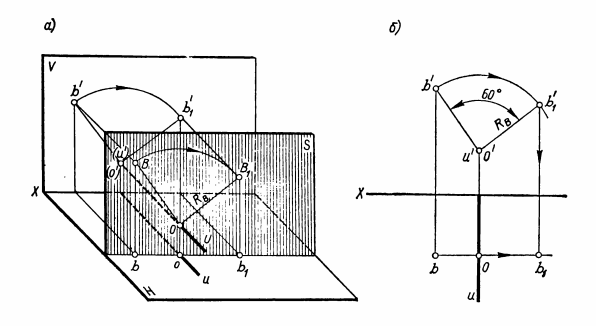 Рис.29 Для лучшего понимания основ способа вращения наденьте на любой стержень (круглый карандаш) колесико, вырезанное хотя бы из картона, отметьте на его ободе точку и проследите за ее вращением. Сначала стержень поставьте перпендикулярно плоскости Н, затем — плоскости V. Простейший случай применения способа вращения — это определение длины отрезка прямой общего положения. Задача решается путем поворота отрезка вокруг оси U⊥ H или U⊥ V до положения, параллельного плоскости проекций. Рассмотрим определение величины отрезка АВ прямой общего положения (рис.30). 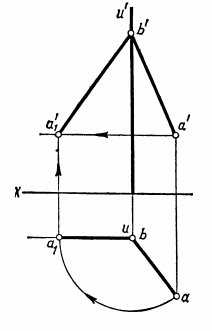 Рис.30 Если ось вращения U задать перпендикулярной плоскости Н, то отрезок АВ следует поворачивать до положения, параллельного плоскости V. Ось вращения удобно проводить через один из концов отрезка, например точку В. В таком случае точка В принадлежит оси вращения и при повороте отрезка остается неподвижной. Таким образом, поворот отрезка АВ сведется к повороту точки А. После поворота горизонтальная проекция а1b отрезка АВ должна быть параллельной оси Х, поэтому проведем через точку b прямую, параллельную оси X, и отложим на ней отрезок a1b = ab. Затем построим фронтальную проекцию а1' точки А1и, соединив ее прямой с точкой b', получим отрезок а1'b', равный длине отрезка АВ. Ось вращения в частном случае может принадлежать плоскости проекций. Тогда при определении длин отрезков прямых или натуральных величин плоских фигур их поворачивают до совмещения с плоскостью проекций, на которой расположена ось вращения. Такой поворот удобно применять, когда один конец отрезка или хотя бы одна вершина плоской фигуры принадлежит плоскости проекций. Например, при определении длины отрезка АВ прямой общего положения (рис.31,а)ось U взята перпендикулярной плоскости V и проведена через точку А, принадлежащую плоскости Н. Точка А при вращении отрезка остается неподвижной, а точку В поворачивают до совмещения с плоскостью Н. После совмещения точки В с плоскостью Н ее фронтальная проекция — точка b1'— окажется на оси X. Дуга окружности, по которой вращается точка В, без искажения проецируется на плоскость V и величина радиуса ОВ равна длине отрезка а'b'. Поэтому проводят дугу окружности радиуса Rв = а' b'с центром в точке а' (рис.31,б)и на пересечении дуги с осью X получают точку b1'. Горизонтальная проекция дуги вращения точки В — отрезок прямой, проходящей через точку b и параллельной оси X. На пересечении этой прямой с линией связи, проведенной через точку b1', получают точку b1. Отрезок прямой АВ после поворота принадлежит плоскости Н, поэтому |аb1| = |АВ|. 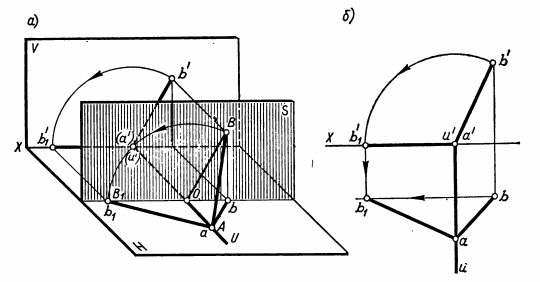 Рис.31 ПЛОСКИЕ ФИГУРЫ Определение натуральной величины плоского многоугольника Плоская фигура проецируется на плоскость проекций без искажения, если она расположена параллельно этой плоскости (см. рис.20,в, 21,в и 22,в). Поэтому, чтобы определить натуральную величину плоской фигуры, надо спроецировать ее на дополнительную плоскость, параллельную заданной фигуре, или повернуть саму фигуру до положения, параллельного плоскости проекций. Например, определим натуральную величину четырехугольника ABCD (рис.32), который расположен перпендикулярно плоскости V и наклонен к плоскости Н. Сначала воспользуемся дополнительной плоскостью Н1 (рис.32,а), которую зададим параллельно плоскости четырехугольника и перпендикулярно плоскости V, т.е. проведем ось проекций X1||a'c'. Для построения проекции четырехугольника на плоскости Н1проведем через точки а', b', с', d' линии связи, перпендикулярные оси Х1. На этих линиях от оси Х1отложим отрезки а1ах1 = аах; b1bх1 = bbх; c1cx1 = ccx; d1dx1 = ddx, взятые с горизонтальной проекции, и получим точки а1, b1, с1, d1. Эти точки последовательно соединим прямыми линиями и получим четырехугольник а1b1с1d1, равный натуральной величине четырехугольника ABCD. 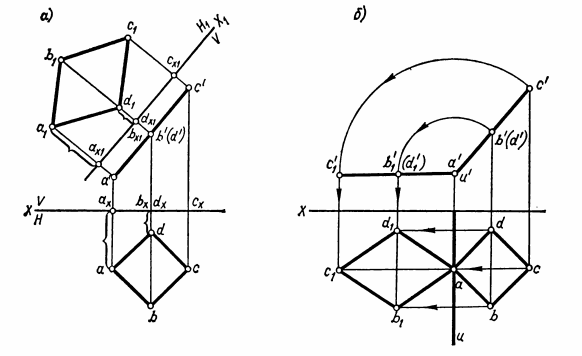 Рис.32 На рис.32,бпоказано определение натуральной величины четырехугольника ABCD путем поворота его до положения, параллельного плоскости Н. Такой поворот можно осуществить вокруг оси, перпендикулярной плоскости V. Если ось вращения провести через одну из вершин, например А, то при повороте она останется неподвижной. При вращении точка С перемещается по дуге окружности радиуса Rc = а'с',а точки В и D — по одинаковым дугам радиуса RB,D = а'b'. Фронтальную проекцию четырехугольника ABCD поворачивают до положения, параллельного оси X. Затем строят его горизонтальную проекцию — четырехугольник аb1с1d1, величина которого равна четырехугольнику ABCD. Построение проекций окружности Окружность проецируется на плоскость проекций без искажения, если она параллельна ей. При этом две другие ее проекции есть отрезки, параллельные осям проекций и по длине равные диаметру окружности. Например, на рис.33 изображена окружность, расположенная в плоскости Т, параллельной плоскости V. 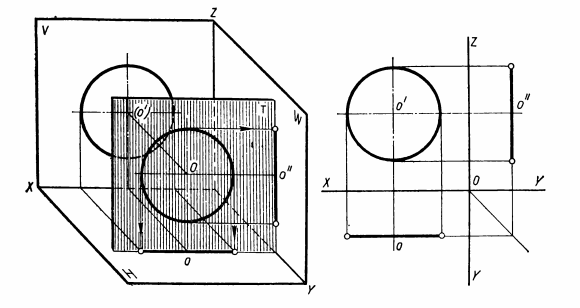 Рис.33 Эта окружность проецируется без искажения на плоскость V, а на плоскости Н и W — в виде отрезков, параллельных соответственно осям X и Z. Если окружность наклонена к плоскости проекций, то ее проекция представляет собой эллипс, большая ось которого равна диаметру окружности. Величина малой оси этого эллипса зависит от угла наклона плоскости окружности к плоскости проекций. Рассмотрим проекции окружности, изображенные на рис.34 Заданная окружность перпендикулярна плоскости V и наклонена к плоскостям Н и W (см. ее фронтальную проекцию), поэтому ее горизонтальная и профильная проекции — эллипсы. Большие оси этих эллипсов представляют собой проекции диаметра окружности, который без искажения проецируется на плоскости Н и W. Таким диаметром является диаметр АВ, перпендикулярный плоскости V и параллельный плоскостям Н и W. Малыми же осями эллипсов являются проекции диаметра CD, перпендикулярного АВ. Величины малых осей определяются с помощью линий связи* проведенных через точки с', d'. Промежуточные точки эллипса построены с помощью дополнительной плоскости проекций Н1. Плоскость Н1 расположена параллельно плоскости окружности, поэтому на нее окружность проецируется без искажения. Сначала строят новую проекцию центра окружности — точку о1и на плоскости Н1описывают заданную окружность. Затем на окружности намечают 10...12 точек и находят их проекции на плоскостях V, Н, W. На рис.34 приведено построение только для двух промежуточных точек 1 и 2. Остальные промежуточные точки строят аналогично точкам 1 и 2.  Рис.34 |
