лекция геометрические тела. Проекционное черчение. Проецирование основных геометрических фигур
 Скачать 1.16 Mb. Скачать 1.16 Mb.
|
|
ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ ЛИНИЙ Прямые линии или их отрезки могут занимать относительно друг друга следующие положения: быть параллельными, пересекаться или скрещиваться. О взаимном положении двух прямых (отрезков) судят по расположению их проекций. Параллельные прямые Если прямые параллельны, то их одноименные проекции параллельны между собой. Например, прямые общего положения АВ и CD (рис.15) параллельны, так как их одноименные проекции параллельны между собой ab||cd, a'b'||c'd' и a''b''||c''d''. Примером параллельных отрезков прямых могут служить боковые ребра призм, образующие цилиндров. 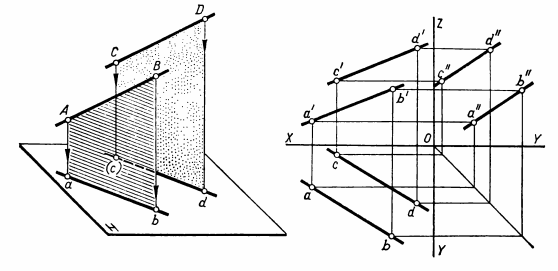 Рис.15 Пересекающиеся прямые Если две прямые пересекаются, то их одноименные проекции также пересекаются и точки пересечения любой пары одноименных проекций располагаются на общей для них линии связи. Такие прямые показаны на рис.16. Прямые общего положения АВ и CD пересекаются между собой, поскольку точки пересечения горизонтальных и фронтальных проекций прямых (k,k'), горизонтальных и профильных (k,k"), фронтальных и профильных (k',k"), лежат на общих линиях связи. Примерами пересекающихся отрезков прямых являются две смежные стороны любого многоугольника или ребра многогранника, сходящиеся в одной вершине. 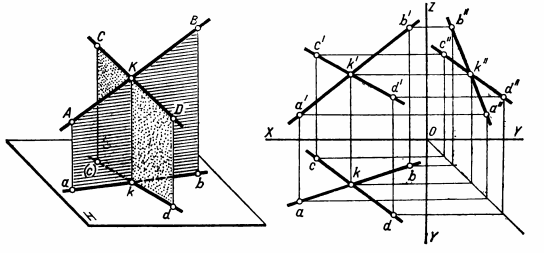 Рис.16 Скрещивающиеся прямые. Если две прямые не параллельны друг другу и не пересекаются, то, следовательно, они скрещиваются (рис.17). Одноименные проекции скрещивающихся прямых могут пересекаться, но в отличие от пересекающихся прямых пара точек пересечения одноименных проекций не лежит на общей линии связи. Это происходит потому, что точка пересечения одноименных проекций скрещивающихся прямых представляет собой проекцию двух точек. Например, точка пересечения горизонтальных проекций аb и cd является проекцией двух точек — М и N. Точка М расположена на прямой АВ, а точка N находится под ней и принадлежит прямой CD. 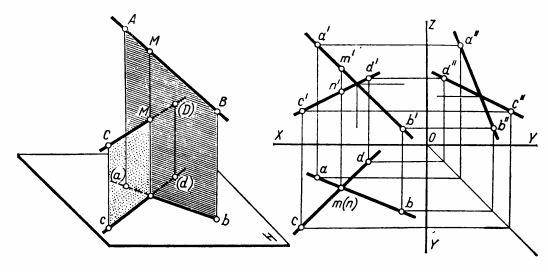 Рис.17 ПРОЕКЦИИ ПЛОСКОСТИ Положение плоскости в пространстве определяют три точки плоскости, не лежащие на одной прямой. Следовательно, чтобы задать проекции какой-либо плоскости Р, достаточно построить проекции трех произвольных ее точек А, В и С, не лежащих на одной прямой (рис.18).  Рис.18 Способы задания плоскости. Если через точки А, В и С (рис.18) провести две пересекающиеся (параллельные) прямые или, последовательно соединив их прямыми, построить треугольник, то проекциями этих прямых и треугольника будет задана та же плоскость Р. Таким образом, проекции плоскости могут быть заданы несколькими способами. Однако чаще всего плоскости задают такими фигурами, как треугольники, трапеции, круги, эллипсы и др. Эти плоские фигуры можно рассматривать как грани призм и пирамид, основания цилиндров и конусов, а также грани и срезы предметов или деталей. В качестве примера на рис.19 плоскость задана треугольником SAB, который является гранью пирамиды. 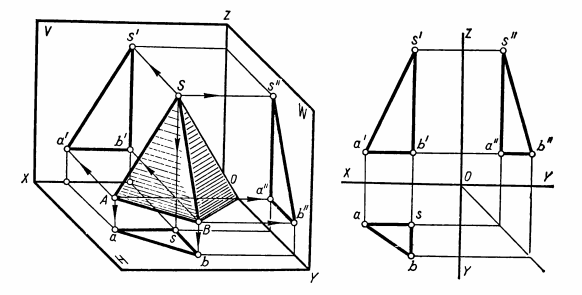 Рис.19 Различные положения плоскости В зависимости от положения заданных плоскостей относительно плоскостей проекций их делят на плоскости общего и частного положения (плоскости уровня и проецирующие плоскости). Плоскости общего положения — плоскости, наклоненные ко всем плоскостям проекций. Плоская фигура, занимающая общее положение (см. рис.19), проецируется на все плоскости проекций с искажением. Плоскости уровня — плоскости, параллельные одной плоскости проекций и перпендикулярные двум другим. По числу плоскостей проекций различают три вида плоскостей уровня. Плоскость, параллельную плоскости Н, называют горизонтальной плоскостью (рис.20,а). Горизонтальная плоскость, перпендикулярна плоскостям проекций V и W и проецируется на них в виде прямых, параллельных осям проекций X и Y (рис.20,б). Проекцию плоскости в виде прямой линии обозначают прописной буквой с индексом плоскости проекций, например, фронтальная проекция горизонтальной плоскости Р обозначается Рy. 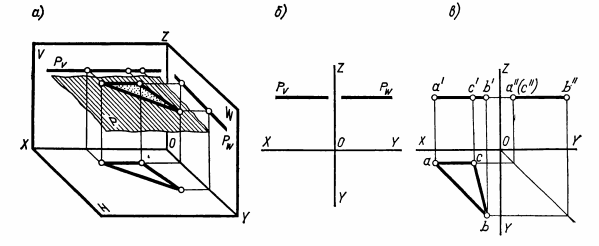 Рис.20 На рис.20,в та же плоскость Р задана проекциями треугольника ABC. Любая фигура, принадлежащая горизонтальной плоскости, например ΔABC, проецируется без искажения на плоскость H, т.е. |Δаbс| = |ΔАВС|. Плоскость, параллельную плоскости V, называют фронтальной плоскостью (рис.21,а). Фронтальная плоскость перпендикулярна плоскостям проекций Н и W. Ее горизонтальная проекция Qнпараллельна оси X, а профильная Qw— оси Z (рис.21,б). 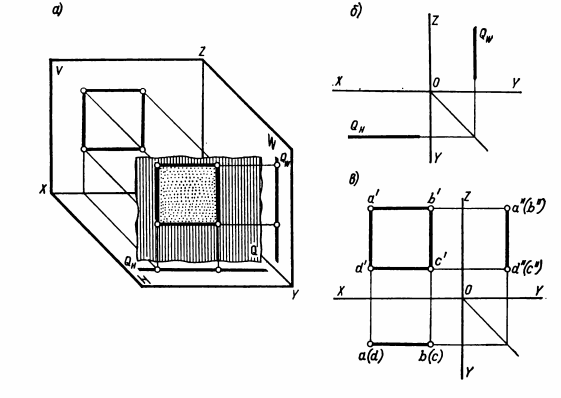 Рис.21 На рис.21,в фронтальная плоскость Q задана плоской фигурой. Фигура, принадлежащая фронтальной плоскости, проецируется без искажения на плоскость V, например квадрат ABCD. Плоскость, параллельную плоскости W, называют профильной плоскостью (рис.22,а). Профильная плоскость перпендикулярна плоскостям проекций Н и V и проецируется на них в виде прямых, параллельных соответственно осям проекций Y и Z (рис.22,б). 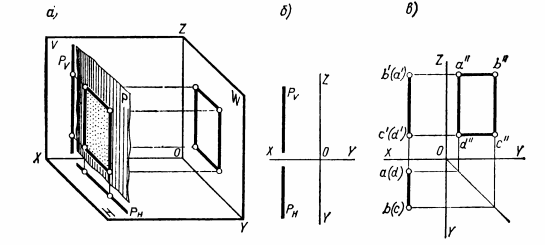 Рис.22 На рис.22,в профильная плоскость задана прямоугольником ABCD. Фигуры, расположенные в профильных плоскостях, проецируются без искажения на плоскость W. Из описания плоскостей уровня видно, что они обладают общими свойствами: 1). плоскости уровня, перпендикулярные двум плоскостям проекций, проецируются на них в виде прямых, параллельных осям проекций; 2). одна проекция плоскости уровня, к плоскости которой она перпендикулярна, определяет ее положение относительно плоскостей проекций; 3). фигуры, принадлежащие плоскостям уровня, проецируются без искажения на параллельную им плоскость проекций. Проецирующие плоскости — плоскости, перпендикулярные одной плоскости проекций и наклоненные к двум другим. Плоскость, перпендикулярная плоскости Н и наклоненная к плоскостям V и W, называется горизонтально-проецирующей (рис.23,а). Горизонтально-проецирующая плоскость Р, перпендикулярная плоскости Н, проецируется на нее в виде прямой Рн. По горизонтальной проекции горизонтально-проецирующей плоскости можно судить о наклоне ее к плоскостям V и W. Угол между ее горизонтальной проекцией Рни осью X равен углу между плоскостями Р и V, а угол между Рни осью Y равен углу наклона плоскости Р к плоскости W (рис.23,б). 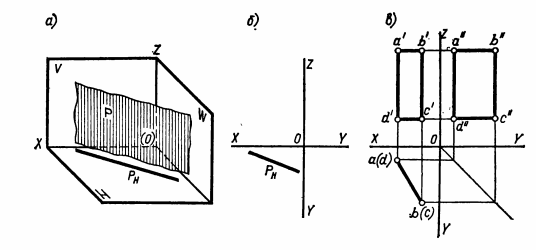 Рис.23 Плоская фигура, задающая горизонтально-проецирующую плоскость, например прямоугольник ABCD (рис.23,в), проецируется на плоскости V и W, с искажением, а на плоскость Н — в виде отрезка ab прямой. Величина искажения зависит от угла наклона проецирующей плоскости к данной плоскости проекций. В рассматриваемом случае прямоугольник ABCD искажен в меньшей степени на профильной проекции, так как с плоскостью W он составляет меньший угол, чем с плоскостью V. Плоскость, перпендикулярная плоскости V и наклоненная к плоскостям Н и W, называется фронтально-проецирующей (рис.24,а). 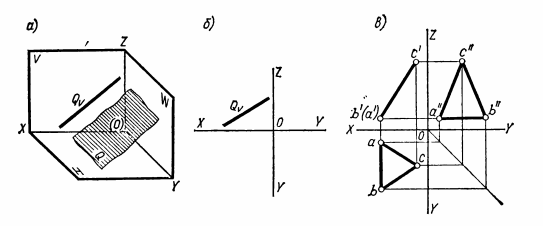 Рис. 24 Для фронтально-проецирующей плоскости характерно, что ее фронтальная проекция представляет собой прямую линию. Независимо от способа задания фронтально-проецирующей плоскости Q (рис.24,б и в)по ее фронтальной проекции всегда можно судить о наклоне плоскости Q к плоскостям проекций Н и W. Угол между фронтальной проекцией Qy(или отрезком а'b') и осью X равен углу между плоскостями Q и H, а угол между Qvи осью Z равен углу наклона плоскости Q к плоскости W. Плоская фигура, принадлежащая фронтально-проецируюшей плоскости, например треугольник ABC (рис.24,в), проецируется на плоскости Н и W с искажением, а на плоскость V — в виде отрезка прямой. Плоскость, перпендикулярная плоскости W и наклоненная к плоскостям Н и V, называется профильно-проецирующей (рис.25,а). Профильно-проецирующая плоскость проецируется на плоскость W в виде прямой линии Pw, которая составляет некоторые углы с осями Y и Z (рис.25,б). О величине углов наклона профильно-проецирующей плоскости к плоскостям Н и V судят по наклону ее профильной проекции соответственно к осям Y и Z. Если профильно-проецирующая плоскость задана плоской фигурой (рис.25,в), то эта фигура проецируется с искажением на плоскости Н и V, а на плоскость W — в виде отрезка прямой. 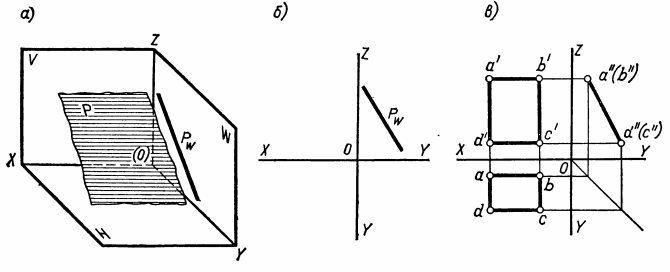 Рис.25 Выводы о свойствах проекций проецирующих плоскостей: 1). Проецируюшая плоскость проецируется в виде прямой на ту плоскость проекций, которой она перпендикулярна. Углы между прямой, представляющей проекцию плоскости, и двумя осями проекций равны углам наклона данной плоскости к двум плоскостям проекций. 2). Проецирующую плоскость можно задавать одной проекцией на ту плоскость проекций, которой она перпендикулярна. 3). Фигуры, расположенные в проецирующих плоскостях, на две плоскости проекций - проецируются с искажением, на одну — в виде отрезка прямой, совпадающего с проекцией плоскости. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ При изображении различных геометрических фигур всегда стремятся располагать их по отношению к плоскостям проекций так, чтобы они занимали частные положения. Это позволяет непосредственно по проекциям судить о размерах и форме изображаемых фигур, определять взаимное положение фигур, а также решать другие метрические задачи. В тех случаях, когда не удается расположить изображаемую фигуру или отдельные ее части (например, ребра, грани) в частных положениях, для решения метрических задач прибегают к преобразованию проекций. Преобразование проекций осуществляют способом перемены плоскостей проекций и способом вращения. Способ перемены плоскостей проекций Способ заключается в том, что изображаемую фигуру (отрезок прямой, многоугольник, тело), не меняя ее положения в пространстве, проецируют на новую дополнительную плоскость проекций, заменившую одну из основных плоскостей Н или V. Дополнительная плоскость проекций образует с плоскостями Н или V новые системы двух взаимно перпендикулярных плоскостей проекций. Положение дополнительной плоскости проекций выбирают в зависимости от поставленной задачи. Сущность способа перемены плоскостей проекций рассмотрим на примере определения длины отрезка АВ прямой общего положения (рис.26,а). Известно, что отрезок прямой проецируется на плоскость проекций без искажения, если он ей параллелен. Поэтому для определения длины отрезка прямой необходимо задать дополнительную плоскость, например V1параллельную отрезку АВ. Плоскость V1должна быть также перпендикулярна плоскости Н. Расстояние от плоскости V1до отрезка АВ выбирают произвольно. Плоскости проекций Н и V1образуют новую систему двух взаимно перпендикулярных плоскостей проекций H/V1. Плоскости Н и V1 пересекаются по прямой Х1— новой оси проекций. В данном примере новая ось X1||ab. 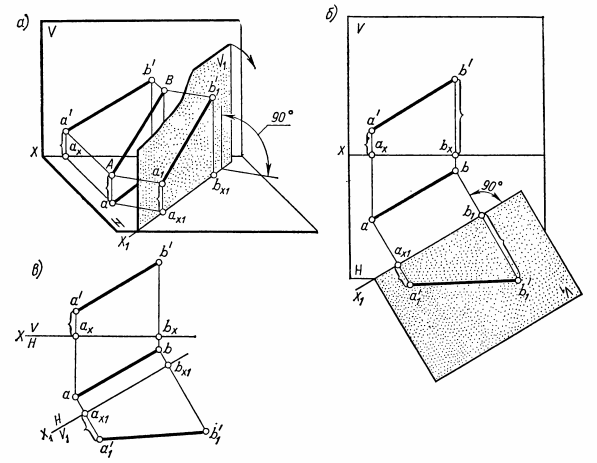 Рис.26 В новой системе плоскостей проекций Н/V1горизонтальная проекция ab отрезка АВ уже построена. Проекцию же отрезка АВ на дополнительную плоскость V1строят обычным путем. Через точки А и В проводят прямые, перпендикулярные плоскости V1 и в пересечении этих прямых с плоскостью V1получают новые проекции точек А и В. Их обозначают а1' и b1'. Соединив точки а1' и b1' прямой линией, получают новую проекцию отрезка АВ, равную его длине, так как отрезок АВ параллелен плоскости V1 Чтобы получить все изображения отрезка АВ на одной плоскости, плоскость V1совмещают с плоскостью Н путем поворота ее вокруг оси Х1. Затем плоскости V1 и Н совмещают с плоскостью V путем поворота их вокруг оси X. После совмещения (рис.26,б) линии связи, соединяющие точки а и а1', а также точки b и b1', должны быть перпендикулярны оси Х1. Точки а1' и b1' удалены от новой оси проекций Х1на то же расстояние, что и точки а' и b' от оси X, т.е. |а1'ax1| = |а'ах| и \ b1'bx1| = |b'bx|. Обычно основную и новую системы плоскостей проекций показывают упрощенно одними осями проекций X и Х1, около которых указывают обозначения плоскостей проекций (рис.26,в). Таким образом, определение длины отрезка АВ прямой общего положения с помощью дополнительной плоскости V1,параллельной отрезку прямой и перпендикулярной плоскости Н, сводится к следующим построениям. Параллельно горизонтальной проекции аb отрезка АВ и на произвольном расстоянии от нее проводят новую ось Х1. Около оси Х1пишут обозначения плоскостей Н и V1, определяя тем самым направление совмещения плоскостей проекций. Плоскости надо совмещать так, чтобы новая проекция не накладывалась на заданную. Затем через точки а и b проводят линии связи, перпендикулярные оси Х1, и на них в направлении совмещения откладывают отрезки: а1'ах1 = а'ах и b1'bx1 = b'bx. Соединив прямой точки а1' и b1', получают длину отрезка, т.е. |а1'b1'| = |AB|. Задача по определению длины отрезка прямой общего положения может быть решена также с помощью дополнительной плоскости проекций, перпендикулярной плоскости V и параллельной отрезку. Пусть требуется определить длину отрезка CD прямой общего положения (рис.27,а). Дополнительную плоскость Н1располагают параллельно отрезку CD и перпендикулярно плоскости V. Расстояние от плоскости Н1до отрезка CD по-прежнему берут произвольно. Однако это расстояние желательно задавать небольшим, так как в противном случае проекции займут много места. 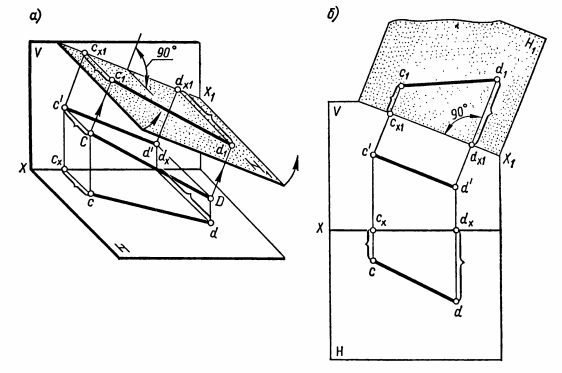 Рис.27 Плоскости H1 и V образуют новую систему плоскостей проекций с осью X1 — линией пересечения плоскостей Н1и V. В данном случае ось Х1расположена параллельно фронтальной проекции отрезка, т. е. X1||c'd'. В новой системе H1⊥ V, у отрезка CD фронтальная проекция c'd' задана и остается построить только его проекцию на плоскости Н1. Для этого через точки С и D проводят проецирующие прямые, перпендикулярные плоскости Н1, и в пересечении их с плоскостью Н1получают новые проекции точек С и D, которые обозначают с1 и d1. Соединив точки с1 и d1 прямой, получают новую проекцию отрезка CD, равную его длине. При введении дополнительной плоскости Н1 расстояние от точек С и D до плоскости V остается неизменным как в основной системе H ⊥ V, так и в новой H1⊥ V, поскольку не меняется положение плоскости V. Это расстояние измеряется отрезками |ссх| = |с1сх1| и |ddx| = |d1dx1| . Чтобы получить совмещенное положение проекций отрезка CD в новой системе H1⊥ V, плоскость Н1поворачивают вокруг оси проекций X1до совмещения ее с плоскостью V. После совмещения (рис.27,б) линии связи, соединяющие точки c' и c1, а также точки d ' и d1, перпендикулярны оси Х1. Проекции без условных ограничений для плоскостей проекций, но с обозначениями плоскостей выполняют так же, как показано на рис.26,в. Таким образом, графическое решение задачи по определению длины отрезка с помощью плоскости Н1, параллельной отрезку и перпендикулярной плоскости V, заключается в следующем. Вначале проводят ось Х1, ипараллельно фронтальной проекции отрезка c'd'и на небольшом от нее расстоянии. Около оси Х1пишут обозначения плоскостей Н1и V. Затем через точки с' и d' проводят линии связи, перпендикулярные оси Х1. На этих линиях связи от оси Х1откладывают два отрезка с1сх1= ссхи d1dx1= ddx. Соединив прямой точки с1 и d1, получают отрезок с1d1, равный длине отрезка CD. |
