ПРОЕКТИРОВАНИЕ И ЛОГИЧЕСКИЙ СИНТЕЗ СУММАТОРАУМНОЖИТЕЛЯ ДВОИЧНО-ЧЕТВЕРИЧНЫХ ЧИСЕЛ. Курсовая работа Сёмин. Проектирование и логический синтез сумматораумножителя двоичночетверичных чисел

• Название: Проектирование и логический синтез сумматораумножителя двоичночетверичных чисел
• Анкор: ПРОЕКТИРОВАНИЕ И ЛОГИЧЕСКИЙ СИНТЕЗ СУММАТОРАУМНОЖИТЕЛЯ ДВОИЧНО-ЧЕТВЕРИЧНЫХ ЧИСЕЛ
• Дата: 08.09.2022
• Размер: 311.66 Kb.
• Имя файла: Курсовая работа Сёмин.docx
• Тип: Пояснительная записка; #667719
• страница: 3 из 6

Минимизация выхода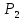

Заменим все конституенты единицы их двоичными номерами (в скобках термы, на которых функция не определена):

К={00100, (00110),01100, (01110)}.

Выполним разбиение комплекса К на группы. Признаком образования i - й группы является количество единиц в двоичном номере конституенты единицы.

Номер группы	Двоичные номера конституент единицы
1	00100
2	(00110), 01100
3	(01110)

Попарно сравним соседние по номеру группы.

К02 К01	(00110)	01100
00100	001*0	0*100

К03 К02	(01110)
(00110)	0*110
01100	011*0

Термы, на которых функция не определена и которые склеились между собой, обозначены серым. Функция на этих наборах переменных должна быть доопределена как имеющая нулевые значения и, следовательно, из дальнейшего рассмотрения должны быть исключены эти импликанты.

Далее формируем новые группы кубов в зависимости от положения свободной координаты и сравниваем их внутри каждой группы.

К12	К14
0*100	001*0
	011*0
0*100	0*1*0

К²₁ = {0*1*0}
Строим импликантную таблицу. Формирование минимального покрытия сводится к выявлению обязательных простых импликант и построению на их основе тупиковых форм.

Простые импликанты	Конституенты единицы
	00100	01100
0*1*0	*	*

F_min = {0*1*0}

F_min =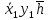

Эффективность минимизации: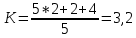

Минимизация выхода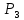

К={00000,(00110),01000,01100,10000,10001,10010,10011,10100,10101, (10110),(10111),11000,11001,11010,11011,11101,(11111)}.

Выполним разбиение комплекса К на группы. Признаком образования i - й группы является количество единиц в двоичном номере конституенты единицы.

Номер группы	Двоичные номера конституент единицы
0	00000
1	01000, 10000
2	(00110), 01100, 10001, 10010, 10100, 11000,
3	10011, 10101, (10110), 11001, 11010
4	(10111), 11011, 11101
5	(11111)

Попарно сравним соседние по номеру группы.

К01 К00	01000	10000
00000	0*000	*0000

К02 К01	(00110)	01100	10001	10010	10100	11000
01000		01*00				*1000
10000			1000*	100*0	10*00	1*000

К02 К03	(00110)	01100	10001	10010	10100	11000
10011			100*1	1001*
10101			10*01		1010*
(10110)	*0110			10*10	101*0
11001			1*001			1100*
11010				1*010		110*0

К03 К04	10011	10101	(10110)	11001	11010
(10111)	10*11	101*1	1011*
11011	1*011			110*1	1101*
11101		1*101		11*01

К04 К05	(10111)	11011	11101
(11111)	1*1111	11*11	111*1

Далее формируем новые группы кубов в зависимости от положения свободной координаты и сравниваем их внутри каждой группы.

К11	К12	К13	К14	К15
*0000	0*000	01*00	100*0	1000*
*1000	1*000	10*00	100*1	1001*
	1*001	10*01	101*0	1010*
	1*010	10*10	110*0	1100*
	1*011	10*11	101*1	1101*
	1*101	11*01	111*1
		11*11
**000	**000	1**00	100**	100**
	1*00*	10*0*	10**0	10*0*
	1*0*0	10**0	1*0*0	1*00*
	1*0*1	10**1	10**1	1*01*
	1**01	1**01	101**	110**
	1*01*	10*1*	1*1*1
		1**11
		11**1

Сгруппируем результаты в группы по положению свободных координат:

1: **000.

2: 1*00*, 1*01*.

3: 1*0*0, 1*0*1, 1*1*1.

4: 1**01, 1**00, 1**11.

5: 10*0*, 10*1*.

6: 10**0, 10**1, 11**1.

7: 100**, 101**, 110**.
Выполним сравнение кубов внутри групп:

2: 1*0**.

3: 1*0**, 1***1.

4: 1**0*, 1***1.

5: 10***.

6: 10***, 1***1.

7: 10***, 1*0**.

К²₁ = {01*00, **000, 1*0**, 1***1, 1**0*, 10***}
Строим импликантную таблицу.

Конституенты единицы	Простые импликанты
	01*00	**000	1*0**	1***1	1**0*	10***
00000		*
01000	*	*
01100	*
10000		*	*			*
10001			*	*	*	*
10010			*			*
10011			*	*		*
10100					*	*
10101				*	*	*
11000		*	*		*
11001			*	*	*
11010			*
11011			*	*
11101				*	*

F_min = {**000, 1*0**, 1**0*}

F_min =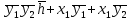

Эффективность минимизации: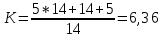



Минимизация выхода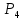

К={00100, (00110), 01001, 01010, 01011, 01101, (01110), (01111), 11001, 11010, 11011, 11100, 11101, (11111)}.

Выполним разбиение комплекса К на группы. Признаком образования i - й группы является количество единиц в двоичном номере конституенты единицы.

Номер группы	Двоичные номера конституент единицы
1	00100.
2	(00110), 01001, 01010.
3	01011, 01101, (01110), 11001, 11010, 11100.
4	(01111), 11011, 11101.
5	(11111).

Попарно сравним соседние по номеру группы.

К02 К01	(00110)	01001	01010
00100	001*0

К03 К02	01011	01101	(01110)	11001	11010	11100
(00110)			0*110
01001	010*1	01*01		*1001
01010	0101*		01*10		*1010

К03 К04	01011	01101	(01110)	11001	11010	11100
(01111)		011*1	0111*
11011	*1011			110*1	1101*
11101		*1101		11*01		1110*

К04 К05	(01111)	11011	11101
(11111)	*1111	11*11	111*1

Далее формируем новые группы кубов в зависимости от положения свободной координаты и сравниваем их внутри каждой группы.

К11	К12	К13	К14	К15
*1001		01*01	001*0	0101*
*1010		01*10	010*1	1101*
*1011		11*01	011*1	1110*
*1101		11*11	110*1
			111*1
*10*1		*1*01	01**1	*101*
*1*01		11**1	*10*1
*101*			*11*1
			11**1

Сгруппируем результаты в группы по положению свободных координат:

1: *10*1, *11*1.

2: *1*01.

3: *101*.

4: 11**1, 01**1.

Выполним сравнение кубов внутри групп:

1: *1**1.

4: *1**1.

К²₁ = {01*10, 001*0, 1110*, *101*, *1**1.}
Строим импликантную таблицу.

Про-стые импли-канты	Конституенты единицы
	00100	01001	01010	010011	01101	11001	11010	11011	11100	11101
01*10			*
001*0	*
1110*									*	*
*101*			*				*	*
*1**1		*		*	*	*		*		*

F_min = {001*0, 1110*, *101*, *1**1}

F_min =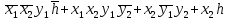

Эффективность минимизации: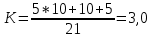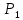


=1

Функциональная схема ОЧУ представлена в графическом приложении