Главная страница
Навигация по странице:

  • Если устройство работает как умножитель

  • Сигналы на входах ФДК Результат на выходах ФДК F

  • 4. Разработка функциональных схем основных узлов 4.1. Логический синтез одноразрядного четверичного умножителя

  • Таблица 3 Мн Мт Упр

    		•

    ПРОЕКТИРОВАНИЕ И ЛОГИЧЕСКИЙ СИНТЕЗ СУММАТОРАУМНОЖИТЕЛЯ ДВОИЧНО-ЧЕТВЕРИЧНЫХ ЧИСЕЛ. Курсовая работа Сёмин. Проектирование и логический синтез сумматораумножителя двоичночетверичных чисел


    Скачать 311.66 Kb.
    НазваниеПроектирование и логический синтез сумматораумножителя двоичночетверичных чисел
    АнкорПРОЕКТИРОВАНИЕ И ЛОГИЧЕСКИЙ СИНТЕЗ СУММАТОРАУМНОЖИТЕЛЯ ДВОИЧНО-ЧЕТВЕРИЧНЫХ ЧИСЕЛ
    Дата08.09.2022
    Размер311.66 Kb.
    Формат файлаdocx
    Имя файлаКурсовая работа Сёмин.docx
    ТипПояснительная записка
    #667719
    страница2 из 6
    1   2   3   4   5   6


    После окончания умножения необходимо оценить погрешность вычислений. Для этого полученное произведение ((Мн*Мт)4=0,13032100002322 РМн*Мт = 6) приводится к нулевому порядку, а затем переводится в десятичную систему счисления:

    (Мн*Мт)4 = 130321,00002322

    (Мн*Мт)10 = 1849.0028

    Результат прямого перемножения операндов дает следующее значение:

    Мн10 · Мт10 = 63,48 * 29,18 = 1849,1724

    Абсолютная погрешность: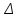

    = 1849,1724 – 1849.0028 = 0,1696

    Относительная погрешность: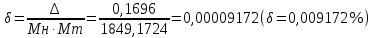



    Эта погрешность получена за счет приближенного перевода из десятичной системы счисления в четверичную обоих сомножителей, а также за счет округления полученного результата произведения.
    3. Разработка структурной схемы сумматора-умножителя
    1 типа для алгоритма умножения "А"

    Если устройство работает как сумматор(на входе Mul/sum – «1»), то оба слагаемых последовательно (за два такта) заносятся в регистр множимого, а на управляющий вход формирователя дополнительного кода (ФДК) F2 и на вход h ОЧУ поступает «1». При поступлении «1» на вход h, ОЧУ не выполняет операцию умножения, а передает без изменения на выход поступившее слагаемое.

    На выходах ФДК формируется дополнительный код одного из слагаемых с учётом знака. Это слагаемое может быть записано в регистр результата, при этом управляющие сигналы, поступающие на входы h всех ОЧУ, дают возможность переписать на выходы ОЧУ разряды слагаемого без изменений (рисунок 3.1).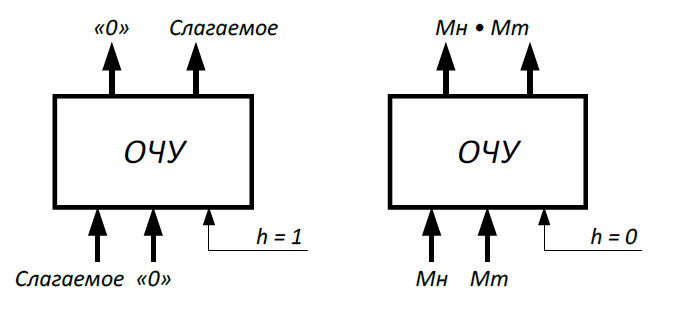



    Рисунок 3.1 – Режим работы ОЧУ
    О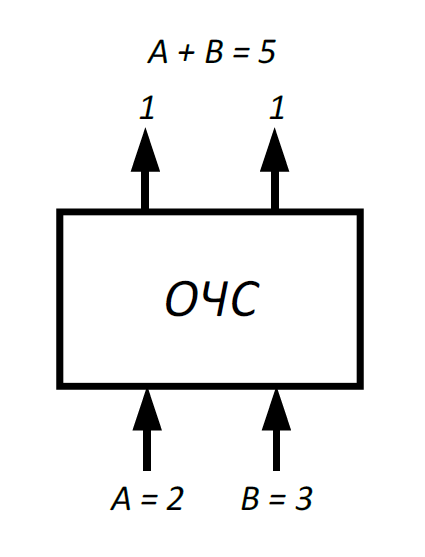
    дноразрядный четверичный сумматор предназначен для сложения двух двоично-четверичных цифр, подаваемых на его выходы (рисунок 3.2).

    Рисунок 3.2 – Одноразрядный четверичный сумматор
    В ОЧС первое слагаемое складывается с нулём, т. к. на старших выходах ОЧУ будут формироваться только коды нуля. Затем первое слагаемое попадает в регистр-аккумулятор, который изначально обнулён.

    На втором такте второе слагаемое из регистра множимого через цепочку ОЧУ и ОЧС попадает в аккумулятор, где складывается с первым слагаемым. Таким образом, аккумулятор (накапливающий сумматор) складывает операнды и хранит результаты.

    Разрядность аккумулятора должны быть на единицу больше, чем разрядность исходных слагаемых, чтобы предусмотреть возможность возникновения переноса при суммировании.

    Если устройство работает как умножитель (на входе Mul/sum – «0»), то множимое и множитель помещаются в соответствующие регистры, а на управляющий вход ФДК F2 поступает «0».

    Диада множителя поступает на входы преобразователя множителя (ПМ). Задачей ПМ является преобразование диады множителя в соответствии с алгоритмом преобразования. При этом в случае образования единицы переноса в старшую диаду множителя она должна быть учтена при преобразовании следующей старшей диады (выход 1 ПМ), т. е. сохраняться до следующего такта на триггер.

    Выход 2 ПМ переходит в единичное состояние, если текущая диада содержит отрицание ( 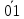). В этом случаи инициализируется управляющий вход F1 формирователя дополнительного кода (ФДК) и на выходах ФДК формируется дополнительный код множимого с обратным знаком (умножение на «-1»).

    Принцип работы ФДК, в зависимости от управляющих сигналов, приведён в таблице 2.
    Таблица 2 – Режим работы формирователя дополнительного кода

    Сигналы на входах ФДК
    Результат на выходах ФДК

    F1
    F2

    0
    0
    Дополнительный код множимого

    0
    1
    Дополнительный код слагаемого

    1
    0
    Меняется знак Мн

    1
    1
    Меняется знак слагаемого


    На выходах 3 и 4 ПМ формируются диады преобразованного множителя, которые поступают на входы ОЧУ вместе с диадами множимого.

    ОЧУ предназначен лишь для умножения двух четверичных цифр. Если в процессе умножения возникает перенос в следующий разряд, необходимо предусмотреть возможность его прибавления.

    Для суммирования результата умножения текущей диады Мн·Мт с переносом из предыдущей диады предназначен ОЧС. Следовательно, чтобы полностью сформировать частичное произведение четверичных сомножителей, необходима комбинация цепочек ОЧУ и ОЧС.

    На четырёх выходах ОЧУ формируется результат умножения диад Мн·Мт. Максимальной цифрой в диаде преобразованного множителя является двойка, поэтому в старшем разряде произведения максимальной цифрой может оказаться только «1»:


    3
    ·
    2
    =
    1 2

    max



    max






    Мн



    Мт







    Это означает, что на младшие входы ОЧС никогда не поступят диады цифр, соответствующие кодам «2» и «3», следовательно, в таблице истинности работы ОЧС будут содержаться 16 безразличных входных наборов.
    Схема электрическая функциональная приведена в графическом приложении.

    4. Разработка функциональных схем основных узлов
    4.1. Логический синтез одноразрядного четверичного умножителя

    ОЧУ - это комбинационное устройство, имеющее 5 входов и 3 выхода:

    • 2 разряда из регистра Мн, преобразованные в ФДК;

    • 2 разряда из регистра Мт, преобразованные в ПМ;

    • управляющий вход h.

    Разряды множителя закодированы в обыкновенной двоичной с/с:

    0 - 00; 1 - 01; 2 - 10; 3 - 11.

    Разряды множимого закодированы в соответствии с заданием:

    0 - 10; 1 - 11; 2 - 01; 3 - 00.

    Управляющий вход h определяет тип операции:

    0 - умножение закодированных цифр, поступивших на информационные входы ОЧУ.

    1 - вывод на выходы без изменения значения разрядов, поступивших из регистра множимого.

    Принцип работы ОЧУ описывается с помощью таблицы истинности (таблица 3).

    В таблице выделено 8 безразличных набора, т.к. на входы ОЧУ из разрядов множителя не может поступить код 11.

    Проведём минимизацию переключательных функций картами Карно-Вейча. Для проведения минимизации переключательных функций необходимо выделить те наборы переменных, где функция принимает единичное значение. Также необходимо включить и все безразличные наборы, то есть наборы, которые не могут прийти на вход схемы ОЧУ.



    Таблица 3

    Мн
    Мт
    Упр
    Старшие разряды
    Младшие разряды
    Пример операции

    в четверичной с/с

    x1
    x2
    y1
    y2
    h
    P1
    P2
    P3
    P4

    0
    0
    0
    0
    0
    1
    0
    1
    0
    3·0=00

    0
    0
    0
    0
    1
    1
    0
    0
    0
    Выход - код «03»

    0
    0
    0
    1
    0
    1
    0
    0
    0
    3·1=03

    0
    0
    0
    1
    1
    1
    0
    0
    0
    Выход - код «03»

    0
    0
    1
    0
    0
    1
    1
    0
    1
    3·2=12

    0
    0
    1
    0
    1
    1
    0
    0
    0
    Выход - код «03»

    0
    0
    1
    1
    0
    0
    1
    1
    1
    3·3=21

    0
    0
    1
    1
    1
    1
    0
    0
    0
    Выход - код «03»

    0
    1
    0
    0
    0
    1
    0
    1
    0
    2·0=00

    0
    1
    0
    0
    1
    1
    0
    0
    1
    Выход - код «02»

    0
    1
    0
    1
    0
    1
    0
    0
    1
    2·1=02

    0
    1
    0
    1
    1
    1
    0
    0
    1
    Выход - код «02»

    0
    1
    1
    0
    0
    1
    1
    1
    0
    2·2=10

    0
    1
    1
    0
    1
    1
    0
    0
    1
    Выход - код «02»

    0
    1
    1
    1
    0
    1
    1
    0
    1
    2·3=12

    0
    1
    1
    1
    1
    1
    0
    0
    1
    Выход - код «02»

    1
    0
    0
    0
    0
    1
    0
    1
    0
    0·0=00

    1
    0
    0
    0
    1
    1
    0
    1
    0
    Выход - код «00»

    1
    0
    0
    1
    0
    1
    0
    1
    0
    0·1=00

    1
    0
    0
    1
    1
    1
    0
    1
    0
    Выход - код «00»

    1
    0
    1
    0
    0
    1
    0
    1
    0
    0·2=00

    1
    0
    1
    0
    1
    1
    0
    1
    0
    Выход - код «00»

    1
    0
    1
    1
    0
    1
    0
    1
    0
    0·3=00

    1
    0
    1
    1
    1
    1
    0
    1
    0
    Выход - код «00»

    1
    1
    0
    0
    0
    1
    0
    1
    0
    1·0=00

    1
    1
    0
    0
    1
    1
    0
    1
    1
    Выход - код «01»

    1
    1
    0
    1
    0
    1
    0
    1
    1
    1·1=01

    1
    1
    0
    1
    1
    1
    0
    1
    1
    Выход - код «01»

    1
    1
    1
    0
    0
    1
    0
    0
    1
    1·2=02

    1
    1
    1
    0
    1
    1
    0
    1
    1
    Выход - код «01»

    1
    1
    1
    1
    0
    1
    0
    0
    0
    1·3=03

    1
    1
    1
    1
    1
    1
    0
    1
    1
    Выход - код «01»


    Следует определить МДНФ для переключательных функций 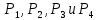, а также эффективность минимизации.

    Минимизацию переключательных функций проводится при помощи метода Квайна – Мак – Класки. Т.к. переключательные функции не полностью определенны, то наборы, на которых они не определены, могут участвовать в склеивании, но в импликантную таблицу не вносятся.
    1   2   3   4   5   6

    написать администратору сайта