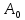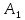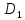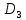ПРОЕКТИРОВАНИЕ И ЛОГИЧЕСКИЙ СИНТЕЗ СУММАТОРАУМНОЖИТЕЛЯ ДВОИЧНО-ЧЕТВЕРИЧНЫХ ЧИСЕЛ. Курсовая работа Сёмин. Проектирование и логический синтез сумматораумножителя двоичночетверичных чисел
 Скачать 311.66 Kb. Скачать 311.66 Kb.
|
4.2 Логический синтез одноразрядного четверичного сумматораОдноразрядный четверичный сумматор (далее – ОЧС) – это комбинационное устройство, имеющее 5 двоичных входов (2 разряда одного слагаемого, 2 разряда второго слагаемого и вход переноса) и 3 двоичных выхода. Принцип работы ОЧС представлен с помощью таблицы истинности (таблица 4). Разряды слагаемого закодированы: 0 – 10; 1 – 11; 2 – 01; 3 – 00. Таблица истинности ОЧС
В таблице 4 выделено шестнадцать безразличных наборов, так как со старших входов ОЧУ не могут прийти комбинации 01 и 00. Минимизацию переключательных функций проведём с помощью карт Карно-Вейча. Символом «x» отмечены наборы, на которых функция может принимать произвольное значение (безразличные наборы). Для функции П
П minДНФ = 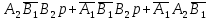 Эффективность минимизации: 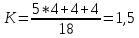 Запишем результат минимизации в логическом базисе ИЛИ, НЕ: П minДНФ = 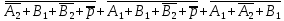  Карта Карно для функции S1: Карта Карно для функции S1:
S1minДНФ = 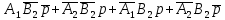 Эффективность минимизации: 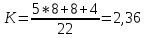 Запишем результат минимизации в логическом базисе ИЛИ, НЕ: S1minДНФ = 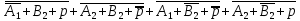 Карта Карно для функции S2:
S2minДНФ = 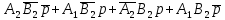 Эффективность минимизации: 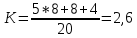 Запишем результат минимизации в логическом базисе ИЛИ, НЕ: S2minДНФ = 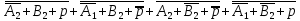 Функциональная схема ОЧС представлена в графическом приложении. 5. Синтез комбинационных схем устройств на основе мультиплексоров 5.1. Смысл мультиплексора Мультиплексор — это логическая схема, имеющая n информационных входов, m управляющих входов и один выход. При этом должно выполняться условие 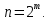 Принцип работы мультиплексора состоит в следующем. На выход мультиплексора может быть пропущен без изменений любой (один) логический сигнал, поступающий на один из информационных входов. Порядковый номер информационного входа, значение которого в данный момент должно быть передано на выход, определяется двоичным кодом, поданным на управляющие входы. На рисунке 5.1 показан мультиплексор, имеющий четыре информационных (или входа данных D0 – D3) и два управляющих (или адресных, А0 и А1) входа, так называемый «один из четырёх». 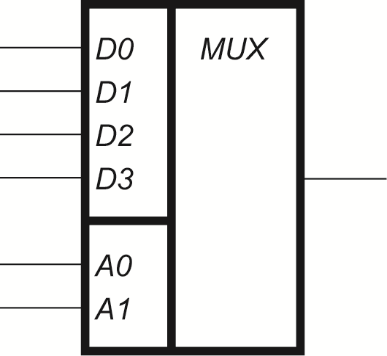 Рисунок 5.1 – Мультиплексор «один из четырёх» В таблице 5.1 определена зависимость выходного сигнала от сигналов на входах мультиплексора. Сигналы 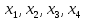 – это логические сигналы, поступающие на вход мультиплексора, которые могут принимать значения нуля или единицы. – это логические сигналы, поступающие на вход мультиплексора, которые могут принимать значения нуля или единицы.Таблица 5.1 – Работа мультиплексора
Из таблицы 5.1 видно, что под действием управляющей комбинации 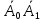 на выход будет пропущен сигнал, поданный на вход на выход будет пропущен сигнал, поданный на вход 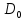 (в данном случае (в данном случае 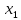 ), а управляющая комбинация ), а управляющая комбинация 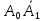 пропускает на выход сигнал, поданный на вход пропускает на выход сигнал, поданный на вход 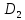 (в данном случае (в данном случае 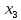 ). ).Мультиплексор может быть использован для синтеза комбинационных схем. С помощью мультиплексора «один из четырёх» легко реализовать любую переключательную функцию (ПФ) от двух переменных. Пример реализации функции «ИЛИ» на мультиплексоре по таблицам истинности (см. таблицу 5.2) приведён на рисунке 5.2. Таблица 5.2 – Функция «ИЛИ»
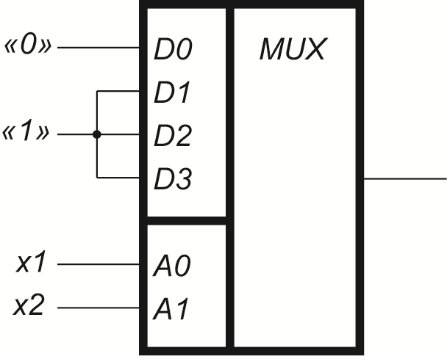 Рисунок 5.2 – Реализация функции «ИЛИ» на мультиплексоре «один из четырёх». На основе мультиплексора можно синтезировать ПФ более чем от двух переменных. Для этого на входе мультиплексора, возможно, придётся разместить некоторую дополнительную логическую схему. Для синтеза этой дополнительной схемы все наборы в таблице истинности целесообразно поделить на группы так, чтобы в каждой группе наборы переменных 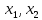 были одинаковы. Таких групп с одинаковыми наборами 00, 01, 10, 11 будет четыре. были одинаковы. Таких групп с одинаковыми наборами 00, 01, 10, 11 будет четыре.Таблицы 5.3 – Таблица истинности для синтеза ПФ от четырёх переменных
Для синтеза входной логической схемы независимыми переменными будут только 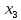 и и 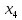 , которые в свою очередь образуют четыре различных набора в каждом группе. , которые в свою очередь образуют четыре различных набора в каждом группе.Записывая для единичных значений ПФ логические выражения для входных переменных 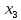 и и 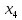 , следует построить по этим выражениям для каждого входа , следует построить по этим выражениям для каждого входа 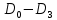 логическую схему. логическую схему.Например, для первой и четвёртой групп: 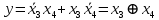 . .Для второй и третьей групп 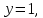 поскольку ПФ на всех восьми наборах равна единице. поскольку ПФ на всех восьми наборах равна единице.Мультиплексор с входной логической схемой для реализации ПФ четырёх переменных показан на рисунке 5.3. 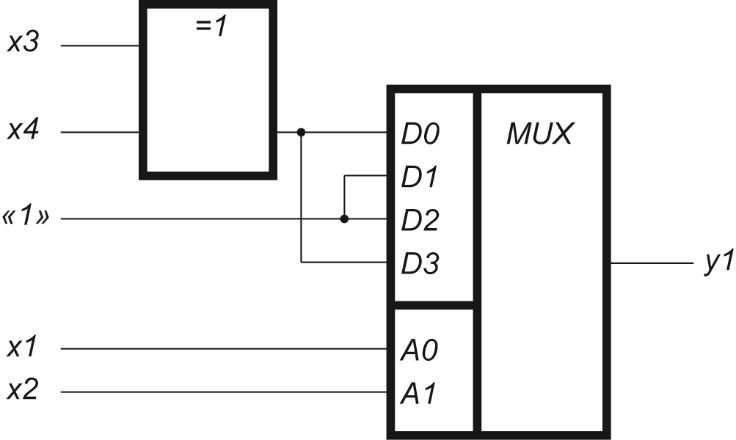 Рисунок 5.3 – Реализация ПФ четырёх переменных | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 X
X 1
1 1
1 X
X
 X
X 1
1 1
1 X
X X
X X
X 1
1