ПРОЕКТИРОВАНИЕ И ЛОГИЧЕСКИЙ СИНТЕЗ СУММАТОРАУМНОЖИТЕЛЯ ДВОИЧНО-ЧЕТВЕРИЧНЫХ ЧИСЕЛ. Курсовая работа Сёмин. Проектирование и логический синтез сумматораумножителя двоичночетверичных чисел
 Скачать 311.66 Kb. Скачать 311.66 Kb.
|
6. Логический синтез преобразователя множителя (ПМ)Преобразователь множителя (ПМ) служит для исключения из множителя диад 11, заменяя их на триады 10  . .Принцип работы ПМ задан таблицей истиности (таблица 6) Таблица 6 – Таблица истинности ПМ
Минимизируем выходные функции 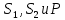 картами Карно. картами Карно.Карта Карно для функции P:
Pmin = qnqn-2 + qnqn-1 Карта Карно для функции S1:
S1min = qnqn-1qn-2 + qnqn-1qn-2 Карта Карно для функции S2:
S2min = qn-1qn-2 + qn-1qn-2 = qn-1  qn-2 qn-2Функциональная схема ПМ представлена в графическом приложении 6. Оценка результатов разработки Быстродействие комбинационной схемы оценивается максимальной задержкой сигнала при прохождении его от входа схемы к выходу, т.е. определяется промежутком времени от момента поступления входных сигналов до момента установления соответствующих значений выходных. Задержка сигнала кратна числу элементов, через которые проходит сигнал от входа к выходу схемы. Поэтому быстродействие схемы характеризуется значением 𝑘∙𝑡эл, где 𝑡эл — задержка сигнала на одном элементе. Значение 𝑘 определяется количеством уровней (рангом) схемы, и рассчитывается следующим образом. Входам приписывается нулевой уровень. Логические элементы, связанные только со входами схемы, относятся к первому уровню. Элемент относится к уровню n, если он связан по входам с элементами нижних уровней. На основе полученных задержек можно определить время умножения на один разряд и на n разрядов множителя): 𝑡𝑛=(𝑡сдв.Мн+𝑡ПМ+𝑡ФДК+𝑡ОЧУ∙𝑚+𝑡ОЧС∙𝑚+𝑡сдв.Мт)∙𝑛, где 𝑡𝑛 — время умножения на n четверичных разрядов множителя; 𝑡сдв.Мн — время сдвига в регистре множимого на один четверичный разряд (два двоичных разряда) вправо; 𝑡ПМ — быстродействие функциональной схемы ПМ; 𝑡ФДК — время работы ФДК; 𝑡ОЧУ — быстродействия функциональной схемы ОЧУ; 𝑚 — количество четверичных разрядов в регистре множимого, количество четверичных разрядов в регистре результата, количество ОЧС и количество ОЧУ; 𝑡ОЧС — быстродействия функциональной схемы ОЧС; 𝑡сдв.Мт — время сдвига в регистре множителя на один четверичный разряд (два двоичных разряда) вверх. Заключение В процессе выполнения курсовой работы была разработана структурная схема сумматора-умножителя первого типа, а также функциональные схемы основных узлов данного устройства. Для уменьшения стоимости логических схем были выполнены минимизации переключательных функций различными способами. Такой подход позволил выявить достоинства и недостатки этих алгоритмов. В качестве главного достоинства минимизации картами Карно-Вейча можно выделить простоту и минимальные затраты времени. Однако применение данного способа для функций многих переменных будет затруднительно. Для минимизации функций многих переменных удобно использовать метод метод Куайна—Мак-Класки. Функциональные схемы были построены в различных логических базисах. Это позволило закрепить теоретические знания основных законов булевой алгебры. Реализация переключательных функций на основе мультиплексоров позволила облегчить процесс минимизации этих функций и упростить функциональную схему одноразрядного четверичного сумматора. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ Искра, Н. А. Арифметические и логические основы вычислительной техники: пособие / Н. А. Искра, И. В. Лукьянова, Ю. А. Луцик. – Минск: БГУИР, 2016. – 75с. Луцик, Ю. А. Учебное пособие по курсу «Арифметические и логические основы вычислительной техники» / Ю. А. Луцик, И. В. Лукьянова, М. П. Ожигина. – Минск: МРТИ, 2001. – 77 с. Савельев, А. Я. Прикладная теория цифровых автоматов / А. Я. Савельев. – М.: Выш. шк., 1987. – 272 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 0
0 1
1 1
1