ПМ. Прикладная механика_пример. Проектирование редуктора одноступенчатого горизонтального привода ленточного конвейера
 Скачать 1.42 Mb. Скачать 1.42 Mb.
|
|
2.4 Расчет предварительных основных размеров колеса  / / ,[1, c.21] (27) ,[1, c.21] (27)где  - делительный диаметр, - делительный диаметр, 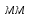 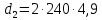 / /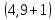 =398,644 =398,644 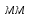 Ширина колеса определяется по формуле [1, c.16] 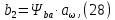  мм ммПринимаем по [1, c.48, таблица 19.1]  96мм не стандартное значение 96мм не стандартное значение 2.5 Расчет и выбор по СТ СЭВ модуля передачи 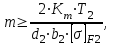 [1,с.22] (30) [1,с.22] (30)где  - коэффициент модуля, для косозубых колес – 5,8. - коэффициент модуля, для косозубых колес – 5,8. Принимаем по рекомендации [1, с.22] модуль передачи  мм. мм.2.6 Определение суммарного числа зубьев и предварительного угла накл. βmin = arcsin(4m/b2)=arsin(4 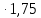 /96)=4,18 /96)=4,18 <8 <8 принимаем βmin=8 принимаем βmin=8 предварительно принимают 100 предварительно принимают 100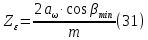 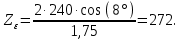 Принимаем 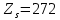   передачи косозубые с таким углом наклона не делают, интервал от 80 до 180 передачи косозубые с таким углом наклона не делают, интервал от 80 до 1802.7 Определение числа зубьев шестерни и колеса Число зубьев шестерни рассчитываем по [1, с.22] 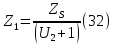 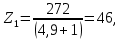 Принимаем  =46. =46.Число зубьев колеса по [1, с.23]  - - (33) (33) 2.8 Определение фактического передаточного числа Фактическое передаточное число определяется по [1, с.23]: 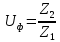 (34) (34) Отклонение от передаточного отношения определяется по [1, с.23]:  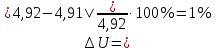 2.9 Определение геометрических размеров колес   делительный диаметр, делительный диаметр,  диаметр вершин, диаметр вершин,  диаметр впадин, диаметр впадин, 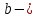 ширина зубчатого колеса ширина зубчатого колесаРисунок 1 – Основные размеры зубчатого колеса Делительный диаметр шестерни по [1, c.23]: 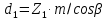 , (36) , (36) = 81,181 = 81,181 , ,Делительный диамет колеса по [ 1, c. 23]:  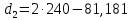 = 398,819 = 398,819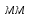 , ,Диаметры окружностей вершин и впадин зубьев колеса и шестерни по [1, c. 23]: 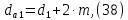 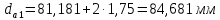 , ,  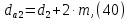 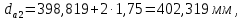   2.10 Определение усилий в зацеплении Окружная сила по [1, c. 24]: 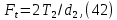 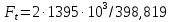 = 6995,65Н. = 6995,65Н.Радиальная сила по [1, c. 24]:  (43) (43)В соответствии с рекомендацией[1, c. 24] для стандартного угла:  , , 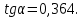  Н. Н.Осевая сила: 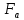 = = 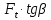 , ,  2.11 Проверка зубьев колеса по напряжениям изгиба Расчетное напряжение изгиба в зубьях колеса по[1, . 15]:  где  – коэффициент, учитывающий распределение нагрузки между зубьями, – коэффициент, учитывающий распределение нагрузки между зубьями,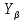 – коэффициент, учитывающий распределение нагрузки по длине зуба, – коэффициент, учитывающий распределение нагрузки по длине зуба, - коэффициент, учитывающий распределение нагрузки по длине зуба, - коэффициент, учитывающий распределение нагрузки по длине зуба, - коэффициент, учитывающий окружную скорость колес, - коэффициент, учитывающий окружную скорость колес, - коэффициент, учитывающий форму зуба. - коэффициент, учитывающий форму зуба.Определяем окружную скорость колеса по [1, c. 25]: 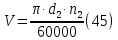  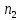 = 66,3 об/мин (см. п.р. 1.9), = 66,3 об/мин (см. п.р. 1.9),V = 3,14 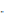 398,819 398,819 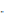 66,3/ 60000 = 1,4м/с 66,3/ 60000 = 1,4м/с Ft = 6995,65 Н (см. п.р. 1.10), b2 =96 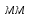 (см. п.р. 2.4), (см. п.р. 2.4),m = 2  (см. п.р. 2.5). (см. п.р. 2.5).По рекомендации [1, с . 25] для косозубых передач:  По рекомендации [1, с . 25] :  , (46) , (46)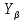 = =  / /   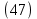  Значение коэффициента Значение коэффициента  принимают по рекомендации [1, с . 26] при HB≤350 для косозубых передач: принимают по рекомендации [1, с . 26] при HB≤350 для косозубых передач: По рекомендации [1, с . 26]:  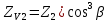 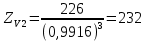 . .По найденому значению  согласно рекомендации [1,с.26, таблица 2.5]принимаем коэфиициент согласно рекомендации [1,с.26, таблица 2.5]принимаем коэфиициент = 3,61. = 3,61. Расчетное напряжение изгиба в зубьях шестерни раситываем по формуле [1, с . 26]: 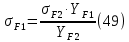  , (50) , (50)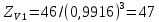 По найденому значению  согласно рекомендации [1,с.26, таблица 2.5] принимаем коэффициент фрмы зуба согласно рекомендации [1,с.26, таблица 2.5] принимаем коэффициент фрмы зуба = 3,65, тогда: = 3,65, тогда: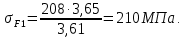 Прочность зубьев колеса по напряжениям изгиба обеспечена, т.к. 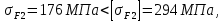  2.12 Проверка зубьев колес по контактным напряжениям Расчетное контактное напряжение определеяем по формуле [1,c. 27]:  где 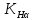 – коэффициент, учитывающий распределение нагрузки мужду зубьями, – коэффициент, учитывающий распределение нагрузки мужду зубьями, - коэффициент, учитывающий распределение нагрузки вдоль линий - коэффициент, учитывающий распределение нагрузки вдоль линий Зацепления, 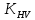 - коэффициент динамической нагрузки - коэффициент динамической нагрузкиd2 = 398,819 мм (см. п.р. 2.9), b2 = 96 мм, 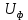 = 4,9 (см. п.р.2.8), = 4,9 (см. п.р.2.8),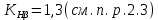 , ,Полученное расчетное контактное напряжение должно находиться в интервале (0,95 ... 1,1). По рекомендации для косозубых колес:  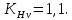 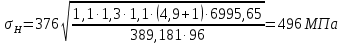  Полученное значение напряжения входит в рекомендуемый интервал, следовательно, контактная прочность колеса обеспечена. 2.13 Основные геометрические параметры зубчатого зацепления
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 мм
мм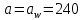 мм
мм , мм
, мм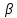 ,
,
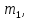 мм
мм мм
мм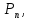 мм
мм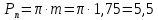 мм
мм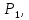 мм
мм мм
мм

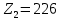
 мм
мм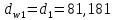

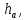 мм
мм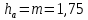 мм
мм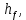 мм
мм мм
мм мм
мм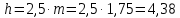 мм
мм мм
мм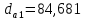 мм
мм
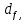 мм
мм мм
мм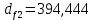 мм
мм
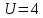 ,9
,9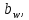 мм
мм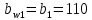 мм
мм мм
мм