Проектирование реверсивного тиристорного преобразователя и пч
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
Энергетические характеристики тиристорного преобразователяЭнергетические характеристики тиристорных преобразователей оцениваются коэффициентом мощности χ и коэффициентом полезного действия η. Коэффициент мощности χ в самом общем случае может быть определён как отношение активной мощности, потребляемой преобразователем P, к полной мощности S (кажущейся мощности для несинусоидальных токов)  (2.5) (2.5)Полная и активная мощности, потребляемые из сети в общем случае несинусоидальных напряжений и токов 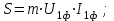 (2.6) (2.6)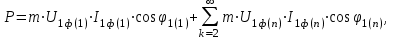 (2.7) (2.7)где  - фазные первичные действующие значения основных гармоник напряжения и тока; - фазные первичные действующие значения основных гармоник напряжения и тока; - действующие значения фазных напряжений и тока высших гармоник; - действующие значения фазных напряжений и тока высших гармоник;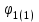 - угол сдвига между векторами основных гармоник фазных напряжений и токов; - угол сдвига между векторами основных гармоник фазных напряжений и токов; - угол сдвига между векторами напряжений и тока высших гармоник. - угол сдвига между векторами напряжений и тока высших гармоник.В случае  , что справедливо для мощных сетей, коэффициент искажения по напряжению , что справедливо для мощных сетей, коэффициент искажения по напряжению  (2.8) (2.8)а по току 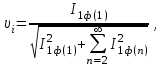 (2.9) (2.9)величина, которого для трёхфазного мостового выпрямителя  . .Активная мощность, потребляемая из сети 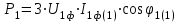 , (2.10) , (2.10)где 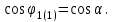 Коэффициент мощности без учёта процесса коммутации определяется по формуле  (2.11) (2.11)Для регулируемого мостового выпрямителя с учётом процесса коммутации (  ) коэффициент мощности определяется по формуле ) коэффициент мощности определяется по формуле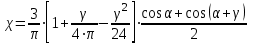 , (2.12) , (2.12)где 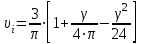 - коэффициент искажения кривой первичного тока с учётом коммутации. - коэффициент искажения кривой первичного тока с учётом коммутации.Активная и реактивная мощности по первой гармонике тока 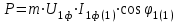 ; (2.13) ; (2.13)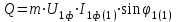 , (2.14) , (2.14)где  ; (2.15) ; (2.15)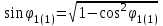 . (2.16) . (2.16)Мощность искажения (дисторции) 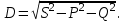 (2.17) (2.17)Порядок расчёта следующий: определяются следующие величины: 1. Первичный линейный ток (обмотка соединена по схеме треугольника) 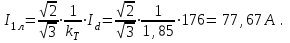 2. Первичный фазный ток  3. Первая гармоника первичного фазного тока 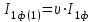 . (2.18) . (2.18)4. Коэффициент искажения по току с учётом коммутации  , (2.19) , (2.19)где γ – угол коммутации,  (2.20) (2.20)Угол регулирования α в расчётах принимается от αmin = 15˚ до αmax = 150,23˚ - βmin = 156˚; p=12 – число пульсаций выпрямленного тока; 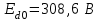 - максимальное значение выпрямленной ЭДС при α = 0; - максимальное значение выпрямленной ЭДС при α = 0; - индуктивное сопротивление фазы трансформатора. - индуктивное сопротивление фазы трансформатора.5. Полная мощность 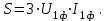 (2.21) (2.21)6. Активная мощность 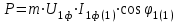 . (2.22) . (2.22)7. Реактивная мощность 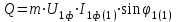 . (2.23) . (2.23)8. Коэффициент мощности 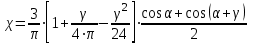 . (2.24) . (2.24)9. Мощность дисторции 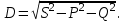 (2.25) (2.25)Результаты расчётов зависимостей S, P, Q, D, χ = 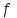 (α) представлены в таблице 2.6 и на рисунке 2.8. (α) представлены в таблице 2.6 и на рисунке 2.8.Таблица 2.6 - Результаты расчёт энергетических характеристик
 Рисунок 2.8 – Энергетические характеристики тиристорного преобразователя Как обычно под КПД подразумевается отношение отдаваемой выпрямителем мощности Pd к потребляемой из сети активной мощности P. 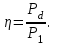 (2.26) (2.26)Для случая работы выпрямителя со сглаженным выпрямленным током, при малой величине пульсаций кривой выпрямленного тока 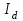 , можно считать, что , можно считать, что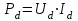 , (2.27) , (2.27)где 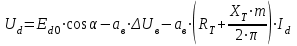 - выпрямленное напряжение на выходе преобразователя; - выпрямленное напряжение на выходе преобразователя; - номинальный ток двигателя. - номинальный ток двигателя.Тогда 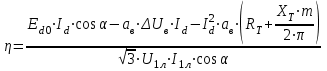 . (2.28) . (2.28)Необходимо определить номинальное значение КПД, рассчитать и построить зависимости  при при 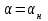 , и , и 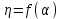 при при  . Исходные данные для расчёта: . Исходные данные для расчёта: 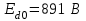 ; ;  ; ; 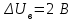 ; ; 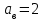 ; ; 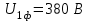 ; ; 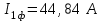 ; ;  ; ; 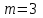 ; ;  ; ; 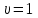 . .Результаты расчётов представлены в таблице. 2.7, 2.8. Примечание. При  преобразователь работает в инверторном режиме и преобразователь работает в инверторном режиме и  . .Таблица 2.7 - Зависимость η = f(Id) при αн = 39,76°
Таблица 2.8 - Зависимость η=f (α) при Id = 176 A, I1ф = 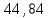 А. А.
По результатам расчёта на рисунке 2.9 и 2.10 построены зависимости  и и 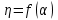 . . Рисунок 2.9 - Зависимость  тиристорного преобразователя тиристорного преобразователя Рисунок 2.10 - Зависимость 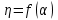 тиристорного преобразователя тиристорного преобразователя |
