Пояснительная записка ПРОЕКТИРОВАНИЕ ТЯГОВОГО ЭЛЕКТРОДВИГАТЕЛЯ. ПЗ_ПРОЕКТИРОВАНИЕ ТЯГОВОГО ЭЛЕКТРОДВИГАТЕЛЯ_Барабанов_48Е. Проектирование тягового электрического двигателя пульсирующего тока

• Название: Проектирование тягового электрического двигателя пульсирующего тока
• Анкор: Пояснительная записка ПРОЕКТИРОВАНИЕ ТЯГОВОГО ЭЛЕКТРОДВИГАТЕЛЯ
• Дата: 01.11.2022
• Размер: 2.85 Mb.
• Имя файла: ПЗ_ПРОЕКТИРОВАНИЕ ТЯГОВОГО ЭЛЕКТРОДВИГАТЕЛЯ_Барабанов_48Е.doc
• Тип: Реферат; #765684
• страница: 3 из 8

. (2.8)

Максимальное число коллекторных пластин оцениваем по (2.3) из [2]:

, (2.9)

Получаем:

.

Определим окружную скорость коллектора при конструктивной скорости электровоза:

, (2.10)



удовлетворяет условиям нормальной работы.

Минимальное число коллекторных пластин оцениваем по (2.5) из [2]:

, (2.11)

где – среднее межламельное напряжение, В.

Среднее межламельное напряжения для двигателей пульсирующего тока должно быть в пределах, указанных в (2.11) из [2], В:

. (2.12)

Пусть , тогда минимальное число коллекторных пластин по (2.12):

.

Полученное количество коллекторных пластин попадает в найденный диапазон значений.
2.3 Расчет размеров проводников обмотки якоря и размеров паза

В проектируемом ТЭД выберем горизонтальное расположение проводников в пазу. Это позволяет значительно уменьшить высоту проводников и уменьшает высоту паза в целом. Это также эффективная мера снижения добавочных потерь в меди.

Линейную нагрузку на якоре машины определяем по формуле (1.3) из [2], А/см:

(2.13)

При подстановке получаем:



Линейная нагрузка током А, полученная в формуле (2.13) попадает в промежуток А= , при , представленным на рисунке 1.1 из [2].

Тепловой фактор определяет в первом приближении нагрев обмотки якоря, поэтому выбор этой величины производим в соответствии с выбранным классом изоляции, класс изоляции В. При величине тепловой фактор лежит в пределах при изоляции В.

Примем .

Размеры меди проводников находятся по допустимой плотности тока, которая зависит от теплового фактора и линейной нагрузки машины. Плотность тока рассчитываем по формуле (1.8) из [2], :

, (2.14)
Получаем:

.

Площадь сечения проводника находим по формуле (2.50) из [2], :

, (2.15)

Получаем:

.

Полюсное деление по якорю определяем по выражению (1.5) из [2], м:

, (2.16)

Получаем:



В работе принята горизонтальная укладка обмотки («плашмя»). Глубина паза ориентировочно оценивается по (2.47) из [2], мм:

, (2.17)

Из формулы (2.16) получаем:

.

Ширину паза выбирают по формуле (2.48) из [2], предварительно так, чтобы:

, (2.18)

Получаем:

.

Зная площадь сечения проводника и пользуясь таблицей 4.2 из [2], подберем примерные значения высоты и ширина проводника по ГОСТу из ряда стандартных: и . Площадь сечения проводника получается

Рассмотрим табличным методом заполнения паза якоря с учетом всей требуемой изоляции и выбранного проводника.

.

Ширина, мм

Медь …………………………………………………………..……………..... 9,3

1. 
   Изоляция проводника – полиамидная лента толщиной 0,05 мм,
   

один слой вполуперекрышу ………………………………………………… 0,2

2. 
   Изоляция корпусная – стеклолента толщиной 0,11 мм,
   

4 слоя вполуперекрышу ……………………………………………………. 1,54

3. 
   Изоляция покровная – стеклолента толщиной 0,1 мм,
   

один слой встык ……………………………………………………. 0,2

4. 
   Зазор на укладку …………………………………………………………. 0,25
   
5. 
   Ширина паза в свету ……………………………………………..…... 11,5
   
6. 
   Припуск на штамповку ………………………………………………….... 0,2
   
7. 
   Ширина паза в штампе ……………………………………….…....... 11,7
   

Высота, мм

Медь ……………………………………………………..……..….....26,24

1. 
   Изоляция проводника – полиамидная лента толщиной 0,2 мм,
   

один слой вполуперекрышу …………………………………………………. 1,6

2. 
   Изоляция корпусная – стеклолента толщиной 0,11 мм,
   

3,5 слоя вполуперекрышу…………………………………………………... 3,08

3. 
   Изоляция покровная – стеклолента толщиной 0,1 мм,
   

один слой встык ………………………………………………….. 0,4

4. 
   Прокладки толщиной по 0,3 мм, две под клин и одна на дно паза ……. 0,9
   
5. 
   Клин…………………………………………………………………………... 4
   
6. 
   Высота паза в свету ………………………………………………….. 36,2
   
7. 
   Припуск на штамповку…………………………………………………..... 0,2
   
8. 
   Высота паза в штампе ………………………………………………... 36,4
   

Правильность выбора и укладки проводника с изоляцией проверяем соотношением: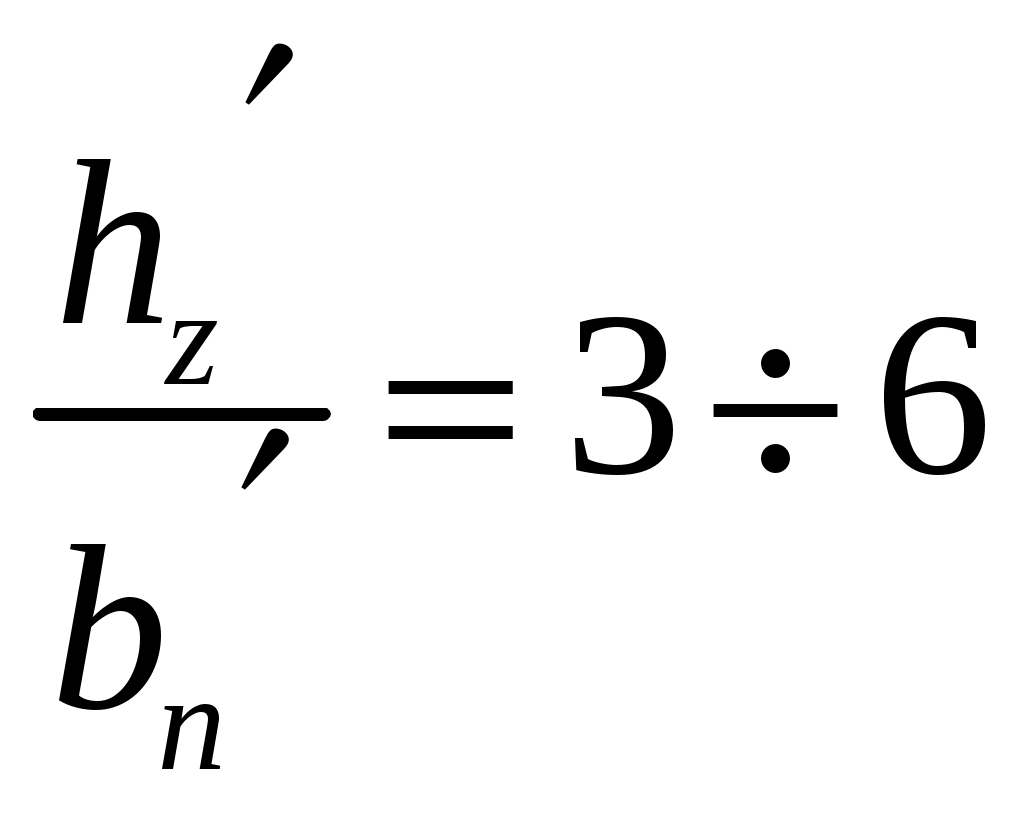

. (2.19)

Для нашего случая: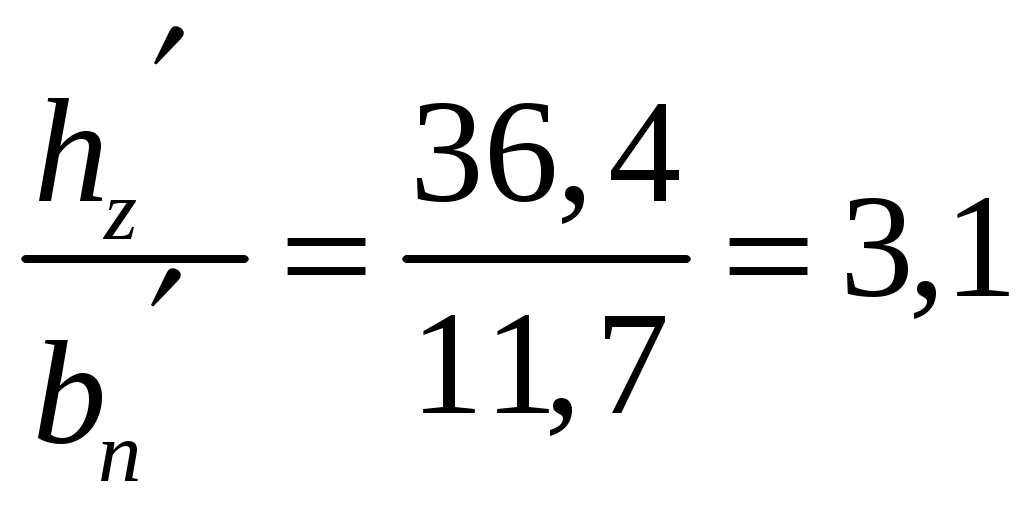

.

Далее в курсовой работе требуется произвести расчет геометрии зубца якоря ТЭД. Его начинают с определения зубцового шага по поверхности якоря по формуле (1.15) из [2], мм:

, (2.20)

При подстановке получим:

.

Ширину головки зубца определяем из выражения, мм:

, (2.21)

Получаем:

.

Зубцовый шаг по дну паза определяем по формуле, мм:

, (2.22)

Получаем:

.

Ширина основания зубца находим из выражения, мм:

, (2.23)

Получаем:



Зубцовый шаг в расчетном сечении определяем по формуле, мм: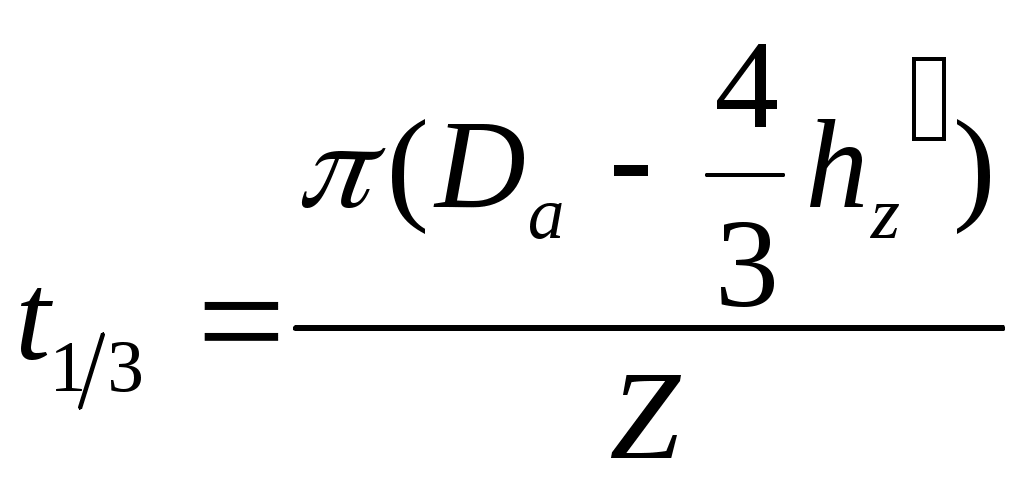

, (2.24)

Получаем: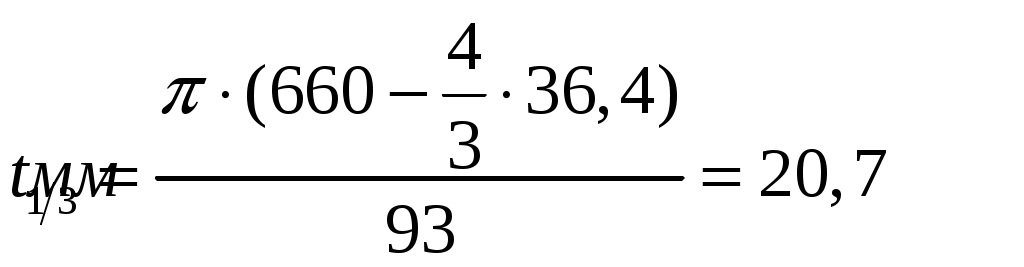



Ширина зубцов в расчетном сечении выражаем по формуле, мм:

, (2.25)

Получаем:



По полученным размерам чертим эскиз паза (рис. 2.1).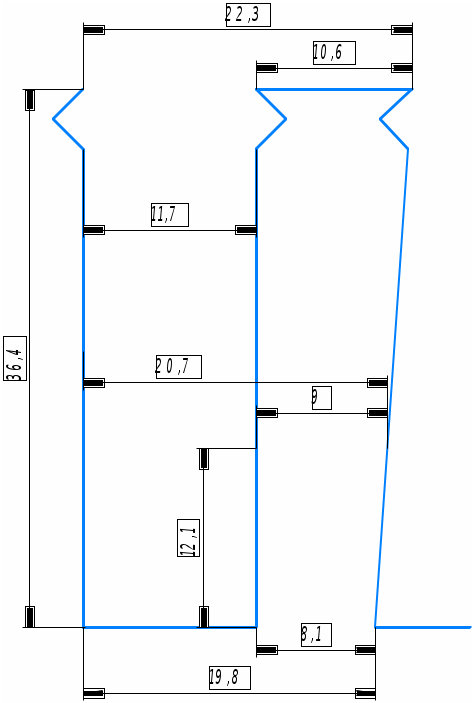


Рисунок 2.1 – Эскиз паза якоря

2.4 Расчет длины пакета стали якоря

На данном этапе проектирования можно определить длину шихтованного пакета якоря , тем самым, проверив правильность намеченных размеров зубца. Для этого необходимо знать индукцию . Для электровозных двигателей эта величина лежит в пределах: (по данным [2]).

Задаем , а в дальнейших расчетах эту величину уточним.

Зная индукцию можно определить величину магнитного потока машины по формуле (2.52) из [2], Вб:

, (2.26)

где – номинальное напряжение на зажимах двигателя, В;

– число параллельных ветвей обмотки;

– число проводников обмотки;

1,03 – коэффициент запаса на производственные неточности;

– частота вращения ТД в номинальном режиме, об/мин.

Подставив данные, получаем:



Длину шихтованного пакета якоря рассчитываем по формуле (2.54) из [2], м:

, (2.27)

где – коэффициент полюсного перекрытия ( =0,66);

– коэффициент заполнения пакета сталью ( =0,97).

Получаем:

Для ТЭД, используемых на ЭПС величина лежит в пределах:

.

Для нашего случая длина шихтованного пакета якоря попадает в заданные пределы. Далее для уточнения индукции в зубцах определяем магнитное сечение зубцов якоря по формуле (2.13) из [1], :

, (2.28)

Получаем:



Расчетная индукция в зубцах по (2.12) из [1] равна, Тл:

, (2.29)

Получаем окончательно:



2.5 Расчет параметров обмотки якоря
Средняя длина одного проводника обмотки якоря определяем по формуле (2.16) из [1], м:

, (2.30)

Получаем:

.

Общая длина провода обмотки якоря по (2.73) из [2] равна, м:

, (2.31)

Получаем:



Масса меди обмотки якоря по (2.74) из [2] равна, кг:

, (2.32)

где – площадь сечения проводника якоря, .

Получаем:



Сопротивление обмотки якоря при определяем по формуле (2.75) из [2], Ом:

, (2.33)

Получаем:



Для удобства дальнейших расчетов сведем основные величины в табл. 2.1.

Таблица 2.1 – Итоговая таблица расчетов

, мм	, мм		,				,	,	,	Ф, Вб		Sz1/3, м2	Bz1/3, Тл
660	400	93	36,4 11,7	372	4	8	3,28 9,3	535,3	5,04	0,075	0,66	0,036	2,11

Первый частичный шаг равно секционной обмотки определяют по формуле (2.57) из [1], в которой - шаг по реальным пазам есть целое число, полученное путем округления величины до ближайшего целого числа:

, (2.34)

Получаем:

.

Второй частичный шаг для простой петлевой обмотки находят по формуле (2.60) из [1]:

(2.35)

Получаем:

.

Пазовое укорочение определяют по формуле:

(2.36)

Получаем:



Укорочение обмотки в коллекторных делениях определяем по формуле:

, (2.37)

Получим:

.

2.6 Расчет параметров уравнительных соединений

Шаг уравнительных соединений определяют по формуле (2.77) из [2]:

, (2.38)

где р число пар полюсов

.

Сечение уравнителя принимают по формуле (2.78) из [2], мм :

, (2.39)

где площадь сечения меди обмотки якоря.

.

Ширина меди проводника принимается равной ширине меди якорной обмотки, т.е. =9,3 мм

Высота меди проводника уравнителя определяется из формулы:

, (2.40)



Округляем до ближайшего размера по ГОСТу,

3 Расчет компенсационной обмотки

Устройство в машине компенсационной обмотки (КО) является наиболее совершенной мерой подавления поперечной реакции якоря, позволяющей снизить максимальные межламельные напряжения приблизительно на 25% в стационарных режимах и на 40 – 50% в переходных.

Применение КО благоприятно и тем, что снижается масса меди обмоток остова. Объясняется это (несмотря на появление дополнительной обмотки) значительным уменьшение числа витков обмоток главных (ГП) и добавочных (ДП) полюсов. Применение КО оправдано при мощностях более 500 кВт

3.1 Расчет параметров компенсационной обмотки

Намагничивающую силу КО определяют, исходя из ее основного назначения – компенсировать намагничивающую силу поперечной реакции якоря на расчетной полюсной дуге. Эта зависимость можно записать в виде выражения (3.1) из [1], А:

, (3.1)

где – намагничивающая сила поперечной реакции якоря, А.

Данную величину находим по формуле (3.2) из [1], А:

, (3.2)

Подставляем данные в формулы (3.2) и (3.1) соответственно и получаем: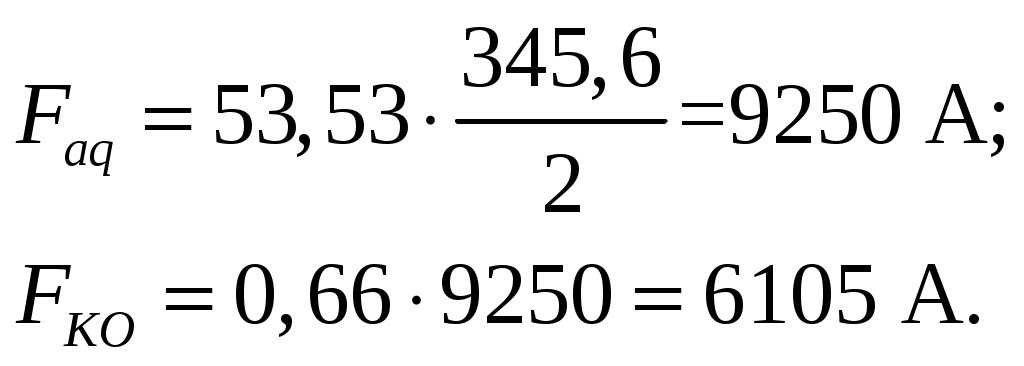



Число витков катушки КО определяется из выражения (3.4) из [1]:

, (3.3)

где – номинальный ток, А;

– число пар параллельных ветвей КО ( =1).

Получаем:

.

Число пазов КО на полюс определяем из условия (3.5) из [1]:

, (3.4)

где N_ZКО – число проводников в одном пазу (задаем ориентировочно N_ZКО=2).



Правильность расчетов проверяется следующими условиями:

• 
  Количество пазов на полюс должно быть целым четным числом ;
  
• 
  Объем тока в пазу КО не должен превышать значения:
  

, (3.5)

Для нашего случая:

• 
  Степень компенсации должна находиться в пределах, определяемых формулой (3.7) из [1]:
  

, (3.6)



3.2 Расчет параметров зубцового слоя компенсационной обмотки

Параметры зубцового слоя КО выбирают исходя из рекомендованного значения индукции в зубце Принимаем

Воздушный зазор машины принимаем

Зубцовое деление рассчитываем по формуле (3.8) из [1], мм:

, (3.7)

Получаем:



Ширину зубца КО определяем по формуле (3.9) из [1], мм:

(3.8)

где – расчетная индукция в воздушном зазоре, Тл;

= 0,95 – коэффициент, учитывающий изоляцию между листами сердечника главного полюса.

Индукцию в воздушном зазоре рассчитываем по выражению из [1], Тл:

, (3.9)

По формулам (3.8) и (3.9) получаем: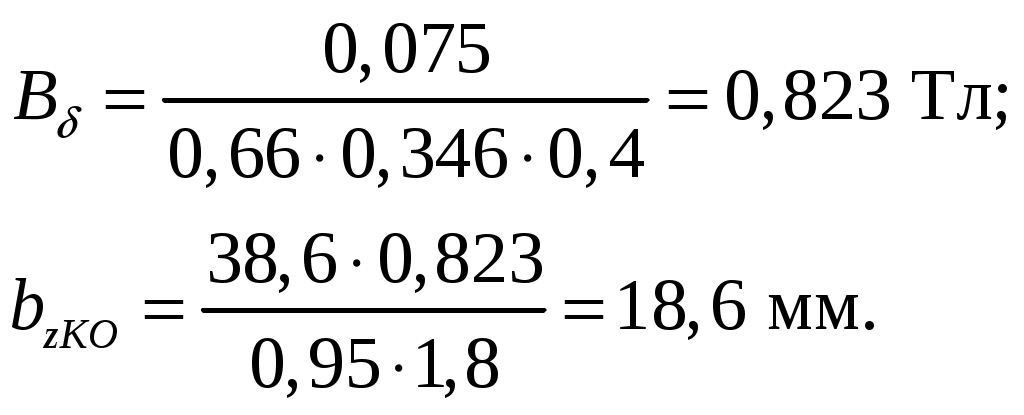



Ширина паза КО определяется по формуле (3.10) из [1], мм:

, (3.10)

Получаем:



Площадь сечения проводника КО предварительно можно рассчитать по формуле (3.11) из [1], :

, (3.11)

где – допустимая плотность тока в КО ( ), .

Получаем:

мм².

Предварительную ширину меди рассчитываем по формуле (3.12) из [1], мм:

, (3.12)

где – толщина изоляции, мм.

Получаем:



Округляем толщину до ближайшего размера, соответствующего ГОСТу

Высота меди КО определяем по формуле (3.13) из [1], мм:

, (3.13)

Получаем:



Округляем толщину до ближайшего размера, соответствующего ГОСТу

Уточняем площадь сечения:

Заполняем паз КО выбранным проводником с использованием требуемой изоляции. Данную операцию производим аналогично проделанной работе для якорной обмотки.

Ширина, мм

Медь …………………..………………….………….…….....……….. 17,2

1. 
   Изоляция проводника – полиамидная лента толщиной 0,05 мм,
   

один слой вполуперекрышу ………………………………...... 0,4

2. 
   Изоляция корпусная – стеклолента толщиной 0,11 мм,
   

4 слоя вполуперекрышу …………………………………...… 1,76

3. 
   Изоляция покровная – стеклолента толщиной 0,1 мм,
   

один слой встык ………………………………………………...….. 0,2

4. 
   Зазор на укладку ………………………………………………………..... 0,64
   
5. 
   Ширина паза в свету ……………………………………………….. 19,56
   
6. 
   Ширина паза в штампе …………………………..…......20,2
   

Высота, мм

Медь …………………………………………………………………...………. 22

1. 
   Изоляция проводника – полиамидная лента толщиной 0,05 мм,
   

один слой вполуперекрышу ……………………………...…... 0,2

2. 
   Изоляция корпусная – стеклолента толщиной 0,11 мм,
   

4 слоя вполуперекрышу …………………………………...….. 1,76

3. 
   Изоляция покровная – стеклолента толщиной 0,1 мм,
   

один слой встык ………………………………………………...…… 0,2

4. 
   Прокладки толщиной по 0,3 мм, две …………………………...….. 0,6
   
5. 
   Клин……………………………………………………………………...…… 5
   
6. 
   Зазор на укладку…………………………………...…………………...….. 0,2
   
7. 
   Высота паза в свету ……………………………………………...… 29,96
   
8. 
   Высота паза в штампе …………………………………….. 30
   

По полученным геометрическим параметрам чертим паз и зубец КО (рис. 3.1).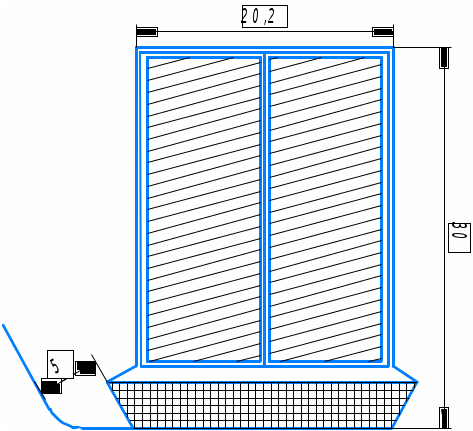


Рисунок 3.1 – Паз и зубец компенсационной обмотки

По полученным значениям размеров паза уточняем расстояние и значение индукции в зубце :

; (3.14)

(3.15)




3.3 Определение сопротивления и массы меди компенсационной обмотки
Длина одного полувитка (стержня) КО может быть рассчитана по формуле (3.16) из [1], м:

, (3.16)

где – длина сердечника главного полюса ( =400), мм.

Получаем:



Длину меди одной катушки КО определяем по формуле (3.17) из [1], м:

, (3.17)

Получаем:



Массу меди КО определяем по формуле (3.18) из [1], кг:

, (3.18)

Получаем:



Сопротивление КО при рассчитываем по формуле (3.19) из [1], Ом:

, (3.19)

где – число параллельных ветвей КО ( =1).

Получаем:



4 Расчет магнитной цепи
Основная цель расчета магнитной цепи ТЭД – определение параметров катушек главных полюсов (ГП), намагничивающая сила (НС) которых обеспечит прохождение по магнитной цепи магнитного потока необходимой величины и построения намагничивающей характеристики, которая является исходной для электромеханических характеристик ТЭД.
4.1 Определение размеров магнитопровода и параметров воздушного зазора
Активную высоту сечения сердечника якоря машины определяем по формуле (2.206) из [2], м:

, (4.1)

где =1,4 Тл – магнитная индукция в сердечнике якоря.

Получаем:



В сердечнике якоря для лучшего охлаждения машины делают аксиальные вентиляционные каналы диаметром , располагая их в рядов. Учитывая пределы, указанные в [2], принимаем и располагаем каналы в два ряда, т.е. .

Учитывая вентиляционные каналы, можно найти конструктивную высоту сечения сердечника якоря по формуле (4.7) из [1], мм:

, (4.2)

Получаем:



Внутренний диаметр сердечника якоря машины определяется формулой (2.211) из [2], м:

(4.3)

где – высота паза якоря, мм:

Получаем: