Пояснительная записка ПРОЕКТИРОВАНИЕ ТЯГОВОГО ЭЛЕКТРОДВИГАТЕЛЯ. ПЗ_ПРОЕКТИРОВАНИЕ ТЯГОВОГО ЭЛЕКТРОДВИГАТЕЛЯ_Барабанов_48Е. Проектирование тягового электрического двигателя пульсирующего тока
 Скачать 2.85 Mb.
|
Диаметр якоря проектируемого ТЭД предварительно рассчитываем по формуле (1.8) из [1], мм: (1.6)где  – коэффициент, зависящий от класса изоляционных материалов, примененных в машине.Приняв класс изоляции В, из [2] определяем ( =130-160) и производим расчет по формуле (1.6) Диаметр якоря должен соответствовать заданной мощности, а его величина выбрана таким образом, чтобы частота вращения якоря соответствовала скорости электровоза, а максимальная окружная скорость не превышала допустимых пределов. При этом диаметр якоря и централь передачи должны быть взаимно связаны по величине отношения  . Однозначного решения эта задача не имеет. Поэтому для оптимального проектирования ТД зададимся несколькими значениями диаметра якоря из полученного интервала и воспользуемся рис. 1.6 из [1]. Результат выбора основных параметров ТД и передачи сведем в таблицу 1.1:Таблица 1.1 – Выбор параметров ТД и передачи
Вариант 1 является самым оптимальным для ТЭД пульсирующего тока. Далее используя данные таблицы, производим окончательное установление параметров двигателя. Вращающий момент на одну пару зубчатых колес рассчитываем по формуле (1.13) из [1] ,  : (1.7)где  – частота вращения якоря в номинальном режиме, об/мин; – для двухсторонней передачи.Получаем:  Используя найденный момент по рис. 2.3 из [2] выбираем нормальный модуль передачи. Получаем:  мм. Тогда торцевой модуль передачи можно найти из отношения (1.15) из [1], мм: (1.8)где  – угол наклона зубьев у тяговой передачи электровоза.Для отечественных электровозов этот угол равен: ψ=24°37’12” или  .Получаем:  .Число зубьев большого зубчатого колеса определяем по формуле (1.14) из [1]:  (1.9)Получаем:  .Так как число зубьев не может быть дробным, то производят округление до ближайшего меньшего целого значения. В таком случае следует уточнить диаметр большого зубчатого колеса по формуле, преобразованной из (1.9):  Число зубьев шестерни рассчитываем по формуле (1.16) из [1]:  , (1.10)где  – передаточное число передачи (берем из таблицы).В результате имеем:  .Число зубьев шестерни округляем до ближайшего большего целого значения. Далее производим уточнение диаметра шестерни, мм:  , (1.11)При подстановке получаем:  .Передаточное число (окончательное):  (1.12)При подстановке получаем:  .Централь зубчатой передачи рассчитываем по формуле (1.17) из [1]:  (1.13)При подстановке получаем:  Проверкой правильности выбора основных параметров двигателя является отношение  , которое должно лежать в рекомендуемых пределах, указанных на рис. 1.6, а из [1]: .Частота вращения якоря двигателя уточняется по формуле (1.11) из [1], об/мин:  , (1.14)Получаем:  Округляем частоту вращения до большего целого числа:  Зная частоту вращения якоря, можем произвести расчет окружной скорости якоря машины в номинальном режиме и режиме максимальной скорости по формулам (1.7) и (1.10) из [1], м/с:  ; (1.15) , (1.16)Получаем:  ; Результаты расчета параметров ТД и тяговой передачи сведен в табл.1.2. Таблица 1.2 – Основные параметры ТД и тяговой передачи
2 Расчет активного слоя якоря 2.1 Определение числа полюсов ТЭД и типа обмотки якоря При проектировании ТЭД следует произвести выбор количества полюсов. Этот процесс проводится с учетом заданной мощности машины. Практика тягового электромашиностроения показала, что при мощности  рекомендуется принимать  . В данной курсовой работе примем это условие.Для ТЭД большой мощности выбираем простую петлевую обмотку. Это позволяет реализовать данную мощность при максимальной частоте вращения, что позволит иметь максимально возможный коэффициент использования мощности  . Кроме этого при выборе данного типа якорной обмотки обеспечивается оптимальная коммутация и равномерное распределение тока в параллельных ветвях обмотки.В итоге получаем следующие данные: обмотка якоря принята простая петлевая равносекционная с уравнительным соединением первого рода, т.е.  . 2.2 Определение числа пазов якоря и числа проводников Расчет обмотки якоря начнем с оценки тока в параллельных ветвях обмотки в номинальном режиме по формуле (2.41) из [2], А:  , (2.1)где  – номинальный ток двигателя, А; – количество параллельных ветвей (принимаем  ).Величину номинального тока находим из выражения (2.38) из [2], А:  (2.2)где  – номинальная мощность двигателя, кВт; – к.п.д. двигателя; – номинальное напряжение на зажимах двигателя, В.Величину к.п.д. оцениваем по номинальной мощности  по рис. 2.4 из [2].Получаем при  –  .Подставляем найденные и исходные величины в формулы (2.2) и (2.1) соответственно и записываем результат: 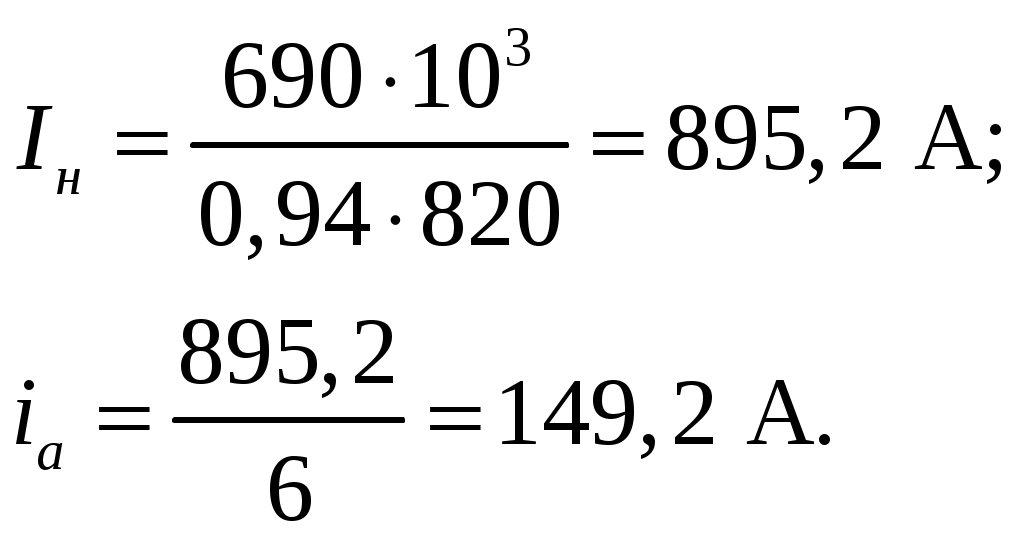 Дальнейший расчет требует определения числа пазов  , числа коллекторных пластин  и числа коллекторных пластин на паз  .Зная диаметр якоря, можно ценить количество пазов по рис. 2.11 из [2]. Получаем при  . Во-первых, такое число удовлетворяет условию  – нечетно для петлевой обмотки. Во-вторых, при меньшем числе пазов возрастает магнитный поток. Выбор величины зависит от величины напряжения на зажимах двигателя. При  Все выше названные величины имеют зависимость вида (2.44) из [2]:  , (2.3)По данной зависимости найдем приближенное число коллекторных пластин:  . Число коллекторных пластин определяет число активных проводников в пазу. Эту зависимость можно описать уравнением (2.45`) из [2]:  , (2.4)Получаем:  По условиям нагревания необходимо, чтобы объем тока в пазу удовлетворял условию (2.46) из [2], А:  . (2.5)Для нашего двигателя:  .Проверка показала, что наши расчеты верны. Число пазов якоря и число проводников обмотки взаимно увязаны между собой соотношением (2.1) из [1]:  , (2.6)где – число пазов; – число проводников.В результате расчета получим:  .Число коллекторных пластин ограничено возможностями практического исполнения коллектора в габаритах ТД, которое связано с диаметром коллектора и коллекторным делением. Поэтому зададимся пределами:  Связь диаметра коллектора и диаметра якоря получаем по (2.15) из [2]:  . (2.7)Тогда по формуле (2.7) получаем  , мм: .Коллекторное деление по конструктивным и технологическим соображениям также ограничено по формуле (2.12) из [2], см: |
,
,
,
,
,
,