расчет траектории двухступенчатой ракеты. Расчет траектории полета двухступенчатой баллистической ракеты -. Программа движения ракеты на аут расчёт баллистического (эллиптического) участка траектории
 Скачать 6.76 Mb.
|
СодержаниеИсходные данные Введение Расчёт активного участка траектории Программа движения ракеты на АУТ Расчёт баллистического (эллиптического) участка траектории Расчёт конечного (атмосферного) участка траектории Коэффициенты перегрузок, действующих на ракету в полёте Упрощенная блок схема решения задачи на ЭВМ Расчёт траектории управляемой БР. Расчёт активного участка траектории Расчёт участка снижения Литература Исходные данные
Введение Баллистические ракеты (БР) дальнего действия и ракеты-носители (РН) космических аппаратов (КА) стартуют вертикально. Вертикальный старт не только обладает рядом преимуществ перед наклонным, но и является единственно возможным для данного класса ракет. Тонкостенная конструкция ракеты не способна противостоять боковым нагрузкам при движении и сходе ракеты с направляющих, а пусковая установка при наклонном старте такого типа ракет по своему весу и габаритам во много раз превышала бы существующие стартовые устройства.  Рис.1. Траектория баллистической ракеты. При вертикальном старте ракета устанавливается на пусковой стол, который снабжен центральным проёмом для выхода газовой струи ракетного двигателя. После старта БР продолжает вертикальный подъём примерно в течении 5..10 сек., после чего начинается её разворот в сторону цели. Траекторию БР (рис.1) можно в первом приближении рассматривать как плоскую кривую. Участок траектории от точки старта О до точки А проходится ракетой с работающим двигателем и называется активным участком траектории (АУТ), или участком выведения. Та часть траектории, где ракета испытывает заметное воздействие аэродинамических сил, называется атмосферным участком полёта. Для тяжёлых БР атмосферный участок всегда короче АУТ. После выключения двигателя (точка А) ракета или головная часть (ГЧ) летит как свободно брошенное тело, и вид траектории полёта определяется только силой притяжения Земли и начальными условиями для этого участка полёта. Участок траектории от точки А до точки С носит название баллистические (эллиптический) участок траектории. Точка С расположена на одинаковой высоте с точкой А. Начальными условиями баллистического участка траектории являются:  - дальность конца АУТ; - высота конца АУТ; - скорость ракеты в точке А; - угол траектории в точке А.Участок траектории от точки С до точки Д носит название участок входа в атмосферу. Так как траектория свободного полёта симметрична относительно большой оси эллипса, то можно принять:  , или  известно из расчётов активного и эллиптического участков траектории; , , .Траектория выведения ракеты-носителя (рис.2), например, двухступенчатой, по своему характеру практически не отличается от траектории БР дальнего действия. В точке А1 заканчивают работу двигатели первой ступени. Блоки первой ступени отбрасываются и падают на Землю (точка С1). Вторая ступень сообщает ракете необходимую скорость, и в конце активного участка второй ступени, уже на орбите, двигатель выключается (точка А2).  Рис.2. Траектория ракеты-носителя. Разворот ракеты на участке выведения осуществляется органами управления по заранее выбранной программе. Выведение ракеты характеризуется программным углом  (угол тангажа) - угол между продольной осью ракеты и линией горизонта точки старта. Зависимость угла от времени полёта называется программой изменения угла тангажа.Полная дальность полёта БР дальнего действия равна:  ,где  - дальность активного участка траектории; - дальность эллиптического участка траектории; - дальность конечного (атмосферного) участка траектории. Расчёт активного участка траектории Допущения, принимаемые при расчёте: Земля имеет форму сферы радиусом  ;Не учитывается влияние вращения Земли  ;Значения параметров атмосферы в точке старта соответствует стандартной атмосфере ГОСТ 4401-81; Ракета стартует с поверхности Земли, т.е.:  ;Вектор тяги двигательной установки направлен по продольной оси ракеты; Управление ракетой на траектории полёта идеальное; Центр давления у ракеты совпадает с её центром масс; При составлении дифференциальных уравнений движения ракеты на АУТ учитывается действие только основных сил, т.е.: а) сила тяги двигательной установки; б) сила притяжения Земли; в) аэродинамическая сила сопротивления воздуха. Управляющие и другие силы, действующие на ракету в полёте, намного меньше основных, и их можно не учитывать. Запишем систему дифференциальных уравнений движения ракеты на АУТ в плоскости стрельбы: и добавим сюда недостающие геометрические соотношения, характеризующие траекторию полёта ракеты  Запишем геометрические соотношения, характеризующие траекторию полёта ракеты в полярной системе:  Из уравнений (3) после интегрирования определяется сферическая дальность полёта на АУТ и местная высота:  Для углов ,  ,  ,  и  могут быть написаны следующие соотношения (рис.3):  Рис.3. Основные силы и моменты, действующие на ракету в полёте. В формулы (1)-(4) входят следующие величины:  - скорость движения ракеты; - осевая аэродинамическая сила; - подъёмная (боковая) аэродинамическая сила; - плотность воздуха на высоте полёта; - плотность воздуха на уровне моря; - площадь миделя ракеты; - диаметр ракеты; - коэффициенты аэродинамических сил сопротивления воздуха, определяются при аэродинамических расчётах. Величины этих коэффициентов - переменные и в основном зависят от скорости или числа Маха  ; - число Маха; - скорость звука в атмосфере на высоте полёта; - масса ракеты; - стартовая масса ракеты; - массовый секундный расход топлива; - время полёта; - вес ракеты; - ускорение земного притяжения на высоте полёта; - ускорение земного притяжения у поверхности Земли; - расстояние от центра Земли до ракеты (радиус-вектор ракеты); - угол атаки, угол между вектором скорости и продольной осью ракеты; - угол наклона траектории, угол между вектором скорости и линией горизонта точки старта; - угол наклона траектории к местному горизонту, угол между вектором скорости и линией местного горизонта; - полярный угол; - тяга двигателя;Тягу двигательной установки в общем случае можно определить по следующей формуле:  , где: - тяга при работе маршевых и управляющих двигателей; - тяга при работе маршевых двигателей; - тяга при работе управляющих двигателей; - удельный импульс тяги маршевых, управляющих двигателей; - массовый секундный расход маршевых, управляющих двигателей; - давление атмосферы на высоте полёта; - площадь среза сопла маршевых и управляющих двигателей; - площадь среза сопла маршевых двигателей; - площадь среза сопла управляющих двигателей;На стадии предэскизного проектирования для ракет с конической головной частью, все ступени которых имеют одинаковый диаметр, могут использоваться следующие зависимости для определения аэродинамических коэффициентов  и  :  Проведя незначительные преобразования уравнений (1)-(3) получим их выражения в виде, удобном для численного интегрирования:  При численном решении системы из 4-х дифференциальных уравнений в любой момент времени легко определить следующие параметры траектории:  Но для определения параметров движения ракеты на АУТ недостаточно полученной системы уравнений (5), так как неизвестно изменение угла атаки и изменение угла тангажа . Поэтому чтобы замкнуть систему (5), к ней необходимо добавить одно из соотношений:а) программное изменение угла тангажа ;б) изменение угла атаки по траектории.Программа движения ракеты на АУТ баллистический ракета запуск перегрузка Анализ реальных программ движения управляемых баллистических ракет (УБР) и ракет-носителей позволяет создать приближенные программы, которые используются при решении задач баллистического проектирования управляемых ракет. Таким образом, для первых ступеней УБР близкой к оптимальной является приближенная программа, описываемая соотношением:  Далее упрощая приближенную программу можно пренебречь величинами углов атаки. В этом случае угол тангажа можно заменить углом траектории и использовать хорошо согласующуюся с реальными приближенную программу вида: где  - угол траектории в конце активного участка; - коэффициент заполнения топливом субракеты; - рабочий запас топлива i-й активной ступени; - стартовая масса i-й активной ступени; - массовый секундный расход топлива i-й активной ступени;Наиболее удобным будет задание различных ограничений на программу движения ракеты на АУТ для некоторых характерных участков траектории в зависимости от количества ступеней ракеты.  Рис.4. Программа угла тангажа и изменения угла атаки для двухступенчатой ракеты. .Двухступенчатая ракета (рис. 4). Расчёты, связанные с выбором оптимальных программ, показывают, что для всех ступеней полёта, начиная со второй, на которые не накладывается ограничений по углу атаки, оптимальная программа весьма близка к прямолинейной. Программа полёта второй ступени включает следующие участки: участок "успокоения" от момента времени  до   , в течении  происходит полёт с углом атаки  . Участок "успокоения" необходим для ликвидации возмущений, возникающих при разделении ступеней;участок доразворота (при необходимости) от момента времени до  . На этом участке  , а угол атаки определяется и выражения участок полёта с постоянным углом тангажа  .Примечание: 3-я и последующие ступени считаем летящими с постоянным углом тангажа.  Рис.5. Основные силы, действующие на ракету при спуске. Расчёт баллистического (эллиптического) участка траектории Положение ракеты в начале эллиптического участка определяется расчетом активного участка траектории и на данном этапе расчёта его можно считать заданным. Движение ракеты от точки  до точки  , расположенных на одинаковой высоте  или одинаковом радиусе  , происходит по дуге эллипса, симметричной относительно оси  (рис.1).Эллиптическая дальность полёта равна:  где  , - константа Земли.Формула для определения оптимального угла траектории в конце активного участка, при котором дальность полёта ракеты на эллиптическом участке будет максимальной.  Сравнивая значение угла  с полученным значением при решении системы уравнений (5), необходимо произвести уточнение программы полёта ракеты на АУТ с целью достижения максимальной дальности полёта БР.Время полёта ракеты на эллиптическом участке:  Расчёт конечного (атмосферного) участка траектории При исследовании параметров движения головной части на атмосферной части пассивного участка траектории необходимо учитывать влияние аэродинамического лобового сопротивления. Движение центра масс головной части относительно не вращающейся Земли при нулевом угле атаки в проекциях на оси скоростной системы координат описывается следующей системой уравнений (рис.6):  где  - масса головной части.Коэффициенты перегрузок, действующих на ракету в полёте При оценке прочности конструкции ракеты необходимо знать не только равнодействующие внешних сил действующих на ракету в целом, но и их отдельные составляющие. При решении системы уравнений (5) или (13) известны тангенциальное  и нормальное  ускорения движения ракеты. Найдём осевую и поперечную составляющие ускорения в связанной системе координат (рис.3). Учитывая, что на массу ракеты, кроме осевых и поперечных ускорений, действует ещё и ускорение земного притяжения, после незначительных преобразований получим коэффициенты суммарной (статической и динамической) осевой  и поперечной  перегрузок действующих на ракету в полёте. Величины и являются чисто траекторными параметрами и определяются в результате численного интегрирования уравнений движения ракеты.Упрощенная блок-схема решения задачи на ЭВМ  Расчет траектории управляемой БР. Расчет активного участка траектории Исходные данные для расчета
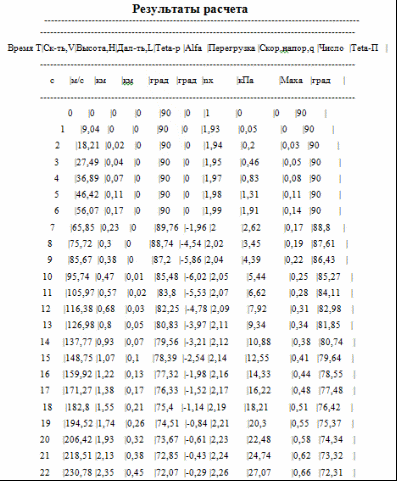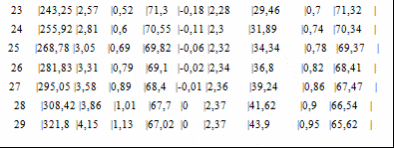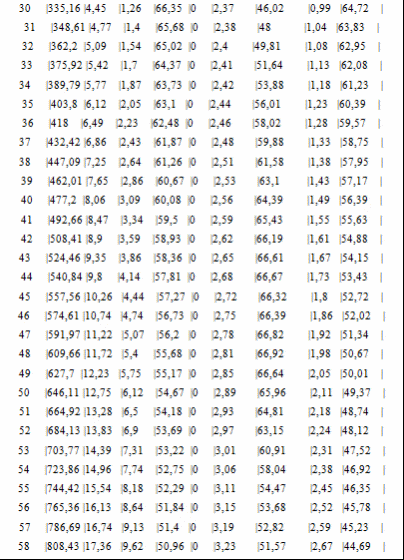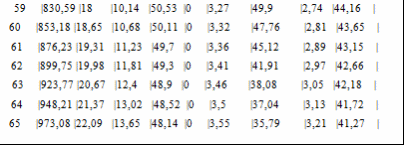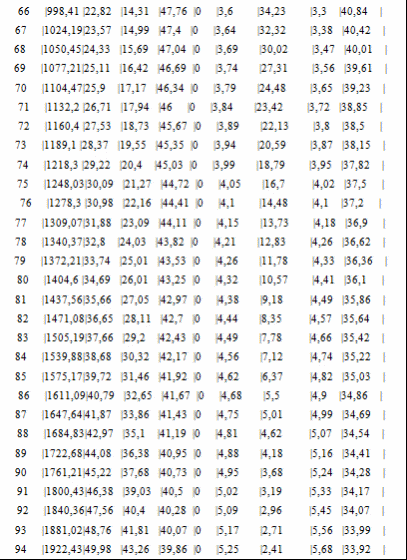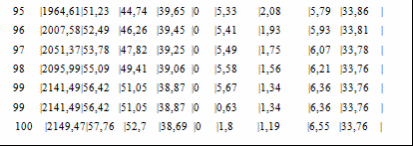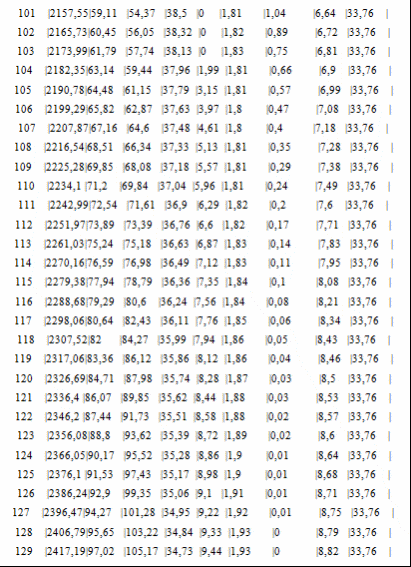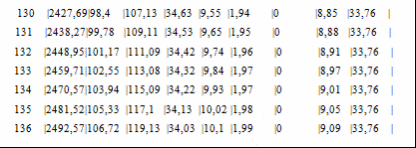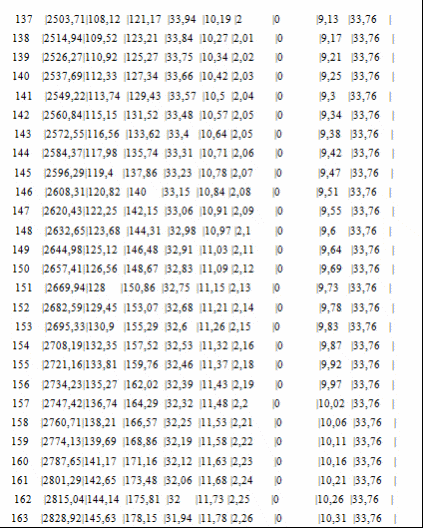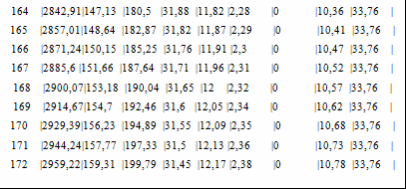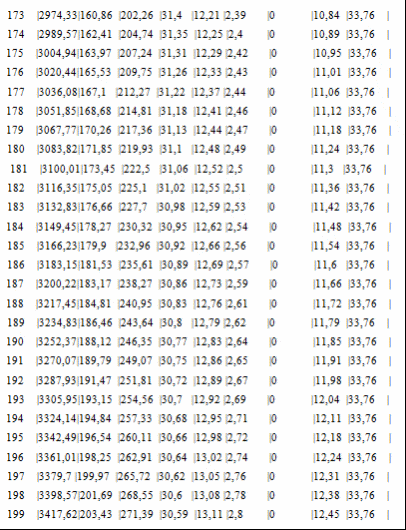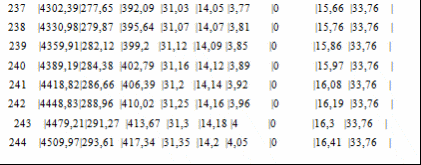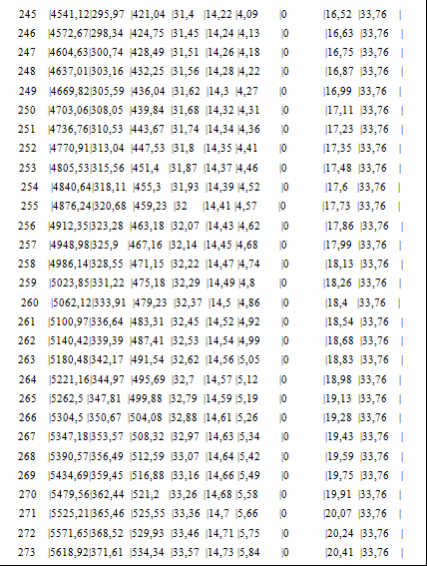             Программа полета ракеты Начало разворота 1 ступени Tpн=6с Конец разворота 1 ступени Tpк=28с Начало разворота 2 ступени Tpн=103с Конец разворота 2 ступени Tpк=275с Начало доразворота 1 ступени Tдp=60с Результаты расчета Скорость Циалковского в конце АУТ Vi=7656м/с Время полета на эллипт. участке Тэл=1348с Угол траект. в конце АУТ ТеtаА=33,79град Оптим. угол трает. в конце АУТ ТеtаК=33,75град Дальность эллипт. участка Lэ=5515км Дальность эллипт. участка при оптим. угле LэO=5515км Макс. высота эллипт. участка Нb=1411км Ошибка по дальности эллипт. участка Dле=-0,01% Расчет участка снижения Исходные данные для расчета
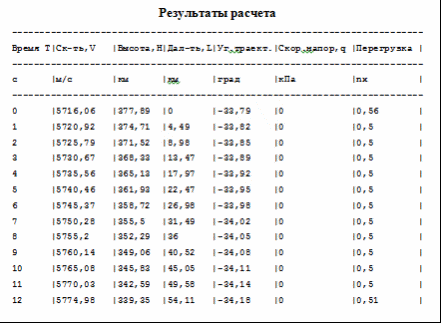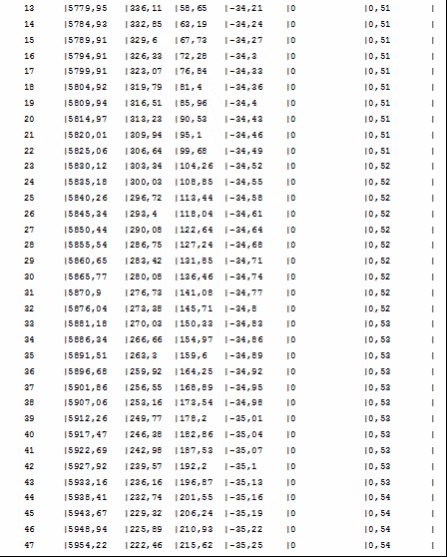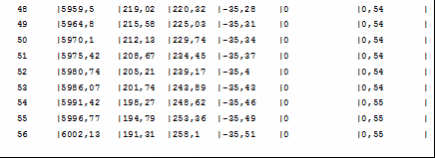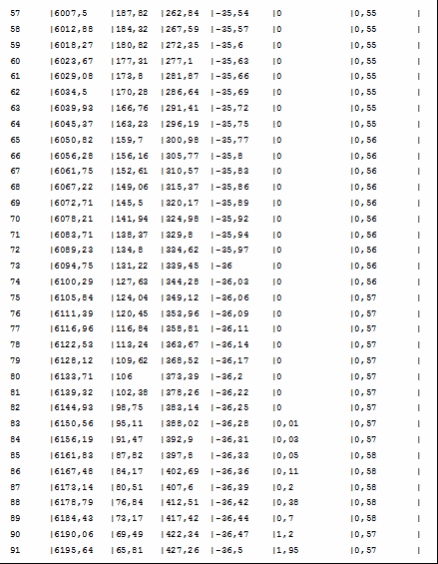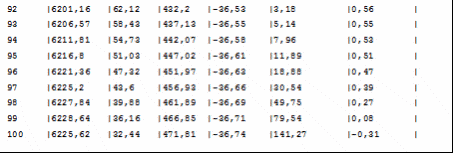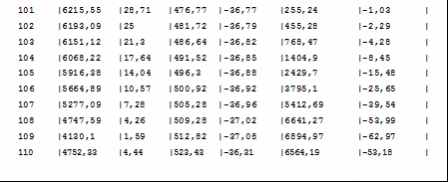      Литература Гречух И.Н. Расчёт траектории баллистических ракет. Методические указания к курсовой работе по специальности 13.06 - Ракетостроение. Омск: ОмГТУ, 1994. 18с. Гречух И.Н. Лекции по предмету «Теория полёта». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||