ГОС. Программирование. Программное обеспечение. Основные этапы решения задач на ЭВМ. Жизненный цикл программного средства
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
2.2. ЛОГИКА ВЫСКАЗЫВАНИ И ПРЕДИКАТОВ. Логическое высказывание – связанное повествовательное предложение, о котором можно сказать истинно оно или ложно (На улице идёт дождь – высказывание, какая хорошая погода – не высказывание). В логике высказываний нас интересует не содержание, а истинностное значение высказываний (0 – Ложь, 1 – Истина). Высказывания А и В равносильны тогда и только тогда, когда истинностные значения А и В совпадают ( 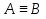 ). ).Основные операции над логическими высказываниями: (см. вопрос 2.1). Логика предикатов –логическая система, средствами которой можно исследовать структуру высказываний. Предикат – свойство объекта (отношения между объектами). Быть чётным, быть простым, делиться, быть больше. 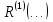 – унарный. – унарный. 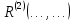 – бинарный. – бинарный.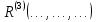 – трёхместный. – трёхместный.Предикат – функция, высказывательные переменные которой принимают значения из некоторого множества 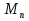 , а сама функция принимает значения {0; 1}. , а сама функция принимает значения {0; 1}.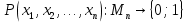 Для задания предиката должно быть задано:
Способы задания предиката.
 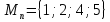 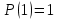 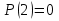 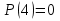 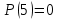
Предикат 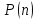 выполняется при выполняется при 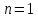 и не выполняется во всех остальных точках x области определения и не выполняется при n = 2,4,5. и не выполняется во всех остальных точках x области определения и не выполняется при n = 2,4,5.
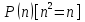 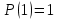 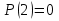 В логике предикатов для образования предложений можно использовать те же логические операции, что и в логике высказываний, т.е. дизъюнкцию, конъюнкцию, эквиваленцию, в результате получаются новые предикаты. 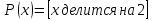 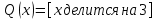 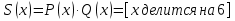 Кванторы.
Операции, уменьшающие местность предиката.
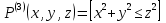 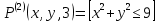 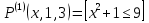 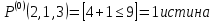
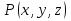 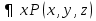 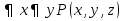 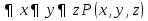 Обобщение логических операций с помощью квантора. Пусть 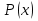 – одноместный предикат, который определён на конечном множестве – одноместный предикат, который определён на конечном множестве 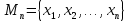 . . 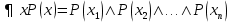 . Квантор общности определяет операцию конъюнкция. . Квантор общности определяет операцию конъюнкция.Квантор существования обобщает операцию дизъюнкция. Основные равносильности алгебры предикатов, содержащие кванторы.
Все законы, которые работают в алгебре высказываний, переносятся в алгебру предикатов.
Алгоритм – эффективная процедура, однозначно приводящая к результату. Основные требования к алгоритму: 1. Каждый алгоритм должен иметь данные: входные, выходные и промежуточные; 2. Данные для своего размещения требуют внутреннюю и внешнюю память; 3. Алгоритм состоит из отдельных элементарных шагов количество, которое конечное; 4. Последовательность шагов алгоритма детерминировано, то есть после каждого шага либо указывается какой шаг делать дальше либо дается команда остановки; 5. Результативность – остановка после конечного числа шагов с указанием того что считать результатом. Алгоритмическая модель – формализация понятия алгоритма. Она является универсальной, то есть допускается описание любых алгоритмов. Выделяют 3 основных типа алгоритмической модели:1. Рекурсивные функции – вычисление и числовые функции; 2. Машина Тьюринга – прообраз современной ЭВМ. В основе лежит представление, а в алгоритме как в некотором детерминированном устройстве способном выполнять в каждый отдельный момент времени лишь примитивные операции; 3. Каноническая система Поста и нормальные алгоритмы Маркова. Преобразование слов в произвольных алфавитах в кот. элементарные операции это подстановки, то есть замены части слова другим словом. Машина Тьюринга представляет собой автомат, с конечным числом состояний, соединенный с внешней памятью – лентой, разбитой на ячейки, в каждой из которых записан один из символов конечного алфавита А= { a1, ... am}. Автомат связан с лентой с помощью головки, которая в каждый момент времени обозревает одну ячейку ленты, и в зависимости от символа в этой ячейке и состояния управляющего устройства записывает в ячейку символ (совпадающий с прежним или пустой), сдвигается на ячейку вправо или влево или остается на месте. Среди состояний управляющего устройства выделим начальное состояние q1 и заключительное состояние qz. В начальном состоянии машина находится перед началом работы. Попав в заключительное состояние, машина останавливается. Т.о. память машины Т – это конечное множество состояний (внутренняя память) и лента (внешняя память). Лента бесконечна в обе стороны, однако в любой момент времени лишь конечный отрезок ленты будет заполнен символами. Поэтому важна не фактическая бесконечность ленты, а ее неограниченность, т.е. возможность писать на ней сколь угодно длинные, но конечные слова. Данные в машине Т– это слова в алфавите ленты; на ленте записываются и исходные данные и окончательные результаты. Элементарные шаги – это считывание и запись символов, сдвиг головки на ячейку влево или вправо, а также переход управляющего устройства в следующее состояние. Детерминированность машины Т определяется следующим образом: для любого внутреннего состояния qi и символаaj однозначно заданы а) следующее состояние qi` б) символ aj`, который надо записать в ту же ячейку вместо aj (стирание – это запись пустого символа ) в) направление сдвига головки dk (L – влево, R– вправо, E – на месте). Это задание может описываться либо системой правил qi aj qi` aj` dk либо таблицей, строкам которой соответствуют состояния, столбцам – входные символы, а на пересечении записана тройка символов qi` aj` dk. либо блок-схемой (диаграммой переходов), в которой состояниям соответствуют вершины, а правилу вида (qi aj qi` aj` dk) – ребро, ведущее из qi в qi` .
Алгоритм имеет сложность O(f(n)), если при увеличении размерности входных данных N, время выполнения алгоритма возрастает с той же скоростью, что и функция f(N). функции, которые чаще всего используются для вычисления сложности. Функции перечислены в порядке возрастания сложности. Чем выше в этом списке находится функция, тем быстрее будет выполняться алгоритм с такой оценкой. 1. C – константа 2. log(log(N)) 3. log(N) 4. N^C, 0 5. N 6. N*log(N) 7. N^C, C>1 8. C^N, C>1 9. N! Самый трудоемкий. Если мы хотим оценить сложность алгоритма, уравнение сложности которого содержит несколько этих функций, то уравнение можно сократить до функции, расположенной ниже в таблице. Например, O(log(N)+N!)=O(N!). Если алгоритм вызывается редко и для небольших объёмов данных, то приемлемой можно считать сложность O(N^2), если же алгоритм работает в реальном времени, то не всегда достаточно производительности O(N). Обычно алгоритмы со сложностью N*log(N) работают с хорошей скоростью. Алгоритмы со сложностью N^C можно использовать только при небольших значениях C. Вычислительная сложность алгоритмов, порядок которых определяется функциями C^N и N! очень велика, поэтому такие алгоритмы могут использоваться только для обработки небольшого объёма данных. Классы сложности. 1. Класс P – задачи, которые могут быть решены за время, полиномиально зависящее от объёма исходных данных, с помощью детерминированной вычислительной машины (например, машины Тьюринга), 2. Класс NP — задачи, которые могут быть решены за полиномиально выраженное время с помощью недетерминированной вычислительной машины, то есть машины, следующее состояние которой не всегда однозначно определяется предыдущими. К классу NP относятся задачи, решение которых с помощью дополнительной информации полиномиальной длины, данной нам свыше, мы можем проверить за полиномиальное время. В частности, к классу NP относятся все задачи, решение которых можно проверить за полиномиальное время. Класс P содержится в классе NP. Классическим примером NP-задачи является задача о коммивояжёре. Работу такой машины можно представить как разветвляющийся на каждой неоднозначности процесс: задача считается решённой, если хотя бы одна ветвь процесса пришла к ответу. Поскольку класс P содержится в классе NP, принадлежность той или иной задачи к классу NP зачастую отражает наше текущее представление о способах решения данной задачи и носит неокончательный характер. В общем случае нет оснований полагать, что для той или иной NP-задачи не может быть найдено P-решение. Вопрос о возможной эквивалентности классов P и NP (то есть о возможности нахождения P-решения для любой NP-задачи) считается многими одним из основных вопросов современной теории сложности алгоритмов. Ответа на этот вопрос нет. Сама постановка вопроса об эквивалентности классов P и NP возможна благодаря введению понятия NP-полных задач. NP-полные задачи составляют подмножество NP-задач и отличаются тем свойством, что все NP-задачи могут быть тем или иным способом сведены к ним. Из этого следует, что если для NP-полной задачи будет найдено P-решение, то P-решение будет найдено для всех задач класса NP. Примером NP-полной задачи является задача о конъюнктивной форме.
Такое определение подчеркивает, что в основу ЭВМ положен принцип программного управления. Один из способов его реализации был предложен в 1945 г. американским математиком Дж. фон Нейманом, и с тех пор неймановский принцип программного управления используется в качестве основного принципа построения ЭВМ. Этот принцип состоит в следующем:
Выборка программы из памяти осуществляется с помощью счетчика команд. Процессор начинает работу после того, как программа записана в память ЭВМ, а в счетчик команд записан адрес первой команды программы. Счётчик команд процессора последовательно увеличивает хранимый в нем адрес очередной команды на длину команды. Работу процессора можно описать следующим циклом: чтение команды из памяти по адресу, записанному в СК, увеличение СК на длину прочитанной команды , выполнение прочитанной команды. А так как команды программы расположены в памяти друг за другом, то тем самым организуется выборка цепочки команд из последовательно расположенных ячеек памяти. Если же нужно после выполнения команды перейти не к следующей, а к какой-то другой, используются команды условного или безусловного перехода, которые заносят в счетчик команд номер ячейки памяти, содержащей следующую команду. Выборка команд из памяти прекращается после достижения и выполнения команды «стоп». Таким образом, процессор исполняет программу автоматически, команду за командой, без вмешательства человека.
Вычислительный процесс должен быть предварительно представлен для ЭВМ в виде программы — последовательности инструкций (команд), записанных в порядке выполнения. В процессе выполнения программы ЭВМ выбирает очередную команду, расшифровывает ее, определяет, какие действия и над какими операндами следует выполнить. Эту функцию осуществляет УУ. Оно же помещает выбранные из ЗУ операнды в АЛУ, где они и обрабатываются. Само АЛУ работает под управлением УУ. Обрабатываемые данные и выполняемая программа должны находиться в запоминающем устройстве — памяти ЭВМ, куда они вводятся через устройство ввода. Данные, которые хранятся на внешних носителях, доступны программе через устройства ввода\вывода. Достоинства и недостатки архитектуры вычислительных машин и систем изначально зависят от способа соединения компонентов. При самом общем подходе можно говорить о двух основных типах структур вычислительных машин и двух типах структур вычислительных систем. Структуры вычислительных машин В настоящее время примерно одинаковое распространение получили два способа построения вычислительных машин: с непосредственными связями и на основе шины. Типичным представителем первого способа может служить классическая фон-неймановская ВМ (рис.). 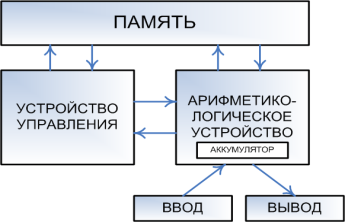 В ней между взаимодействующими устройствами (процессор, память, устройство ввода/вывода) имеются непосредственные связи. Особенности связей (число линий в шинах, пропускная способность и т. п.) определяются видом информации, характером и интенсивностью обмена. Основным достоинством такой архитектуры является возможность расширения узких каналов данных только определенных связей, что экономически может быть наиболее выгодным решением. |

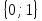 – область значений предиката.
– область значений предиката.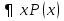 будем подразумевать высказывание, истинное когда
будем подразумевать высказывание, истинное когда 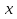 из множества
из множества 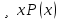 будем подразумевать высказывание, истинное когдасуществует элемент из множества
будем подразумевать высказывание, истинное когдасуществует элемент из множества 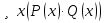 . Существует такое x, которое кратно 2 и кратно 3.
. Существует такое x, которое кратно 2 и кратно 3.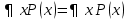 ,
, 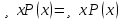 (перенос отрицания).
(перенос отрицания).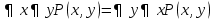 ,
, 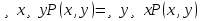 .
.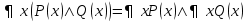 ,
, 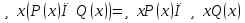
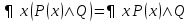 ,
, 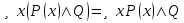 ,
, 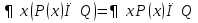 ,
, 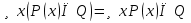 .
.