ГОС. Программирование. Программное обеспечение. Основные этапы решения задач на ЭВМ. Жизненный цикл программного средства
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
3) Третья нормальная форма. Отношение находится в 3НФ тогда и только тогда, когда оно находится во 2НФ и в нем отсутствуют транзитивные зависимости неключевых атрибутов от ключевых. Транзитивной зависимостью неключевых атрибутов от ключевых называется следующая: {A} → {B} и {B} → {C}, где {A} — потенциальный ключ, {B} и {С} — различные множества неключевых атрибутов. Таким образом, отношение в 3НФ содержит только такие неключевые атрибуты, которые находятся в прямой зависимости от ключевых атрибутов. Пример: Отношение (ГРУППА, СЕЦИАЛЬНОСТЬ, ФАКУЛЬТЕТ) ГРУППАСПЕЦИАЛЬНОСТЬ СЕЦИАЛЬНОСТЬФАКУЛЬТЕТ После нормализации: (ГРУППА, СПЕЦИАЛЬНОСТЬ), (СПЕЦИАЛЬНОСТЬ, ФАКУЛЬТЕТ). На практике приведение отношения к 3НФ оказывается достаточным и процесс нормализации на этом заканчивается. Избыточная нормализация может существенно усложнить запросы к базе данных и ее структуру, тем самым понизить ее эффективность.
Физические модели баз данных определяют способы размещения данных в среде хранения и способы доступа к этим данным, которые поддерживаются на физическом уровне. В каждой СУБД по-разному организованы хранение и доступ к данным, однако существуют некоторые файловые структуры, которые имеют общепринятые способы организации и широко применяются практически во всех СУБД. В системах баз данных файлы и файловые структуры, которые используются для хранения информации во внешней памяти, можно классифицировать следующим образом: 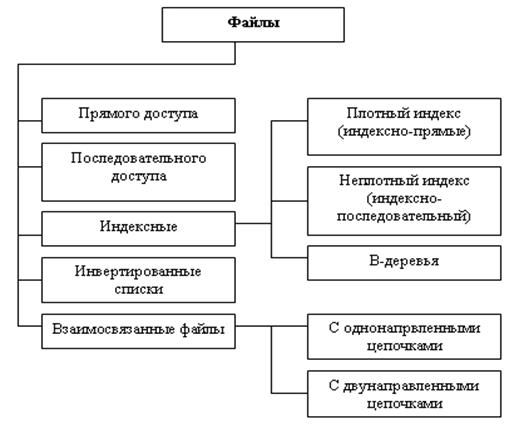 Файлы с прямым доступом обеспечивают наиболее быстрый способ доступа. Мы не всегда можем хранить информацию в виде файлов прямого доступа, но главное – это то, что доступ по номеру записи в базах данных весьма неэффективен. Чаще всего в базах данных необходим поиск по первичному или возможному ключам, иногда необходима выборка по внешним ключам, но во всех этих случаях мы знаем значение ключа, но не знаем номера записи, который соответствует этому ключу. В подобных случаях применяют различные методы хэширования и создают специальные хэш- функции. Несмотря на высокую эффективность хэш-адресации, в файловых структурах далеко не всегда удается найти соответствующую функцию, с помощью которой можно было бы полностью избежать коллизий, поэтому при организации доступа по первичному ключу широко используются индексные файлы. Индексные фaйлы можно представить как файлы, состоящие из двух частей: индексной области и области данных файла (записи БД). В зависимости от организации индексной и основной областей различают 2 типа файлов: с плотным индексом и с неплотным индексом. В файлах с плотным индексом основная область содержит последовательность записей одинаковой длины, расположенных в произвольном порядке, а индексная запись состоит из значения ключа и номера записи: 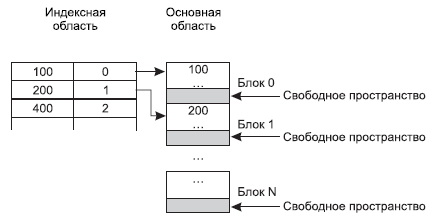 Здесь значение ключа - это значение первичного ключа, а номер записи - это порядковый номер записи в основной области, которая имеет данное значение первичного ключа. Неплотный индекс строится именно для упорядоченных файлов. Для этих файлов используется принцип внутреннего упорядочения для уменьшения количества хранимых индексов. Структура записи индекса для таких файлов состоит из значения ключа первой записи блока и номера блока с этой записью. В индексной области мы теперь ищем нужный блок по заданному значению первичного ключа. Так как все записи упорядочены, то значение первой записи блока позволяет нам быстро определить, в каком блоке находится искомая запись. Все остальные действия происходят в основной области. 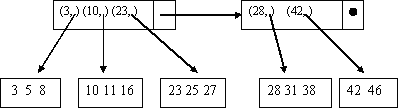 Для обеспечения быстрого доступа к данным на запоминающих устройствах в современных БД используются древовидные структуры данных, хранящиеся во внешней памяти, такие, как B-деревья. Построение В-деревьев связано с простой идеей построения индекса над уже построенным индексом. В общем случае получим некоторое дерево, каждый родительский блок которого связан с одинаковым количеством подчиненных блоков, число которых равно числу индексных записей, размещаемых в одном блоке. Количество обращений к диску при этом для поиска любой записи одинаково и равно количеству уровней в построенном дереве. Такие деревья называются сбалансированными (balanсed) именно потому, что путь от корня до любого листа в этом древе одинаков. 6. КОМПЬЮТЕРНАЯ ГРАФИКА.
Для представления графической информации на двумерной плоскости (например, экране монитора, странице книги и т.п.) в вычислительной технике применяются два основных подхода: растровый и векторный. При векторном подходе графическая информация описывается как совокупность неких абстрактных геометрических объектов, таких как прямые, отрезки, кривые, прямоугольники и т.п. Растровая графика же оперирует растровыми изображениями. Растровое изображение — изображение, представляющее собой матрицу пикселей или цветных точек (обычно прямоугольную). Важными характеристиками изображения являются:
По количеству цветов изображения могут быть:
Цвет любого пиксела растрового изображения запоминается с помощью комбинации битов. Чем больше битов для этого используется, тем больше оттенков цветов можно получить. Под градацию яркости обычно отводится 1 байт (256 градаций), причем 0 – черный цвет, а 255 – белый (максимальная интенсивность). Растр – это порядок расположения точек (растровых элементов). Растр, элементами которого являются квадраты, называется прямоугольным, именно такие растры наиболее часто используются. Растровое представление является естественным в тех случаях, когда нам не известна дополнительная информация об изображаемых объектах (например, цифровым фотоаппаратом можно снимать изображения произвольного содержания). Достоинства растровых изображений:
Недостатки растровых изображений:
Векторная графика — способ представления объектов и изображений в компьютерной графике, основанный на использовании геометрических примитивов, таких как точки, линии, сплайны и многоугольники. Термин используется в противоположность к растровой графике, которая представляет изображение как матрицу фиксированного размера, состоящую из точек (пикселей) со своими параметрами. Как правило, векторное изображение представляет собой набор геометрических примитивов, описываемых их основными параметрами. Сферы применения векторной графики очень широки. Широко используется векторное представление шрифтов. Векторные модели широко применяются в САПР. Они строятся на векторах, занимающих часть пространства в отличие от занимающих все пространство растровых моделей. Это определяет их основное преимущество – требование на порядки меньшей памяти для хранения и меньших затрат времени на обработку и представление, а главное – высокую точность позиционирования и представления данных. Векторным можно назвать только способ описания изображения, а само изображение для нашего глаза всегда растровое. Таким образом, задачами векторного графического редактора являются растровая прорисовка графических примитивов и предоставление пользователю сервиса по изменению параметров этих примитивов. Все изображение представляет собой базу данных примитивов и параметров макета (размеры холста, единицы измерения и т. д.). Преимущества векторной модели изображений:
Фундаментальные недостатки векторной графики.
Различают три вида трехмерных моделей: 1. Каркасная 2. Поверхностная 3. Объемная (твердотельная,Solid) При трехмерном геометрическом моделировании решается одна задача. Определить, принадлежит ли точка телу объекта или находится вне его. Решая однозначно данную задачу, можно алгоритмически построить все другие задачи, связанные с трехмерным моделированием. 1. Каркасная модель состоит из множества трехмерных точек и ребер их соединяющих. Основная задача трехмерной геометрической модели для каркасной модели сводится к тому, что мы можем не только определить, принадлежит ли точка ребру или нет. Достоинство – простота описания. Недостаток – неоднозначное определение трехмерного объекта. Каркасные модели, как правило, используются для быстрой визуализации. 2. Поверхностная модель может быть задана тремя способами: 2.1. Преобразование каркасной модели к поверхностной 2.2. Математический способ 2.3. Кинематический способ В первом виде на каркасной модели через два ребра или три точки проводятся плоскости, определяющие необходимую сложную поверхность. Данная модель также носит название «плоскостная модель». Второй метод (математический) в настоящее время представлен двумя направлениями: R-функциями и NURBS. R-функция представляет из себя полином некоторой степени от координат x и y. Rn(x, y) =a0+a1x+b1y+a2x2+b2y2+…+anxn+bnyn NURBS. Плоские или трехмерные сплайновые поверхности, полученные методом Бизье. Сплайн – плавная кривая, полученная из последовательности непрерывных точек по какому-то методу. Положение точек может быть изменено. Вводятся дополнительные точки, определяющие кривизну сплайна. Эти дополнительные точки строятся автоматически различными методами. NURBSы являются наиболее используемой моделью для построения наиболее сложных поверхностей. Третий метод – кинематический. В данном методе сложная трехмерная поверхность строится из множества простых. Эти поверхности могут быть элементарными (плоскость, шар, тор и т. д.) или полученными сложным методом (вращение, сдвиг, вытяжка). Элементарные геометрические модели соединяются с использованием двух теоретико-множественных операций: объединения и пересечения, а также их комбинаций. В результате получается сложная поверхность, которую можно описать некоторым графом относительно точки начала (центра) плоскости. Достоинства поверхностной модели – относительная простота описаниям в связи с этим несложные алгоритмы для ее получения. Недостатки – высокие требования к вычислительному устройству, неоднозначность. Поверхностная модель наиболее широко используется в рекламных целях и для получения сложных поверхностей с целью получения объемной модели. 3. Объемная модель строится тремя методами: 3.1 Преобразование поверхностной модели в объемную. 3.2 Кинематический. 3.3 Восстановление объема по чертежу. Метод преобразования поверхностной модели к объемной заключается в том, что к поверхности задается вектор по нормали, определяющий положение материала. Достоинства: однозначное определение основной задачи 3D геометрического моделирования. Недостатки : высокая сложность алгоритмов и, как следствие, высокая стоимость ПО. Проекция (лат. projectio — выбрасывание вперёд) — изображение трёхмерной фигуры на так называемой картинной (проекционной) плоскости. Термин проекция также означает метод построения такого изображения и технические приёмы, в основе которых лежит этот метод. Проекционный метод изображения предметов основан на их зрительном представлении. Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой О (центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета. Соединив эти точки прямыми линиями в том же порядке, как они соединены в предмете, получим на плоскости перспективное изображение предмета или центральную проекцию. Если центр проекции бесконечно удалён от картинной плоскости, то говорят о параллельной проекции, а если при этом проекционные лучи падают перпендикулярно к плоскости — то об ортогональной проекции. Проекция широко применяется в инженерной графике, архитектуре, живописи и картографии. Изучением проекций и методов проектирования занимается начертательная геометрия. Однородные координаты — координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число. Однородными координатами вектора (х, у, z) является тройка чисел (x', y', z', w), где х = х' / w, у = y' / w, z = z' / w, а w — некоторое вещественное число (случай, когда w = 0 является особым). Данные координаты не позволяют однозначно задать точку пространства. Например, (1, 1, 1, 1) и (2, 2, 2, 2) задают одну и ту же точку (1, 1, 1). При переходе к однородным координатам для точки с координатами (x, y, z) предлагается взять набор (x, y, z, 1). В процессе преобразований координата w может меняться. Обратный переход к декартовым координатам осуществляется посредством деления на w-координату.
В процессе 3D моделирования создаются геометрические модели, т.е. модели, отражающие геометрические свойства изделий. Различают геометрические модели каркасные (проволочные), поверхностные, объемные (твердотельные). Каркасная модель состоит из множества трехмерных точек и ребер их соединяющих. Для каждой линии известны координаты концевых точек и указана их инцидентность ребрам или поверхностям. Достоинство – простота описания. Недостаток – неоднозначное определение трехмерного объекта. Каркасные модели, как правило, используются для быстрой визуализации. Поверхностная модель отображает форму детали с помощью задания ограничивающих ее поверхностей, например, в виде совокупности данных о гранях, ребрах и вершинах. Поверхностная модель может быть задана тремя способами:
В первом виде на каркасной модели через два ребра или три точки проводятся плоскости, определяющие необходимую сложную поверхность. Данная модель также носит название «плоскостная модель». Второй метод (математический) в настоящее время представлен двумя направлениями: R-функциями и NURBS.R-функция представляет из себя полином некоторой степени от координат x и y. NURBS (Неоднородный рациональный B-сплайн, Non-uniformrational B-spline) - математическая форма, применяемая в компьютерной графике для генерации и представления кривых и поверхностей. NURBS-поверхности являются наиболее используемой моделью для построения сложных поверхностей. Третий метод – кинематический. В данном методе сложная трехмерная поверхность строится из множества простых. Эти поверхности могут быть элементарными (плоскость, шар, тор и т. д.) или полученными сложным методом (вращение, сдвиг, вытяжка). Элементарные геометрические модели соединяются с использованием двух теоретико-множественных операций: объединения и пересечения, а также их комбинаций. |
