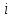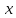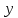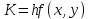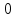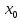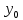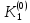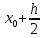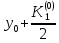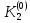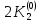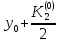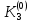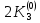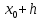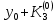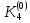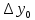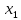Численные методы. Программная реализация решения системы обыкновенных дифференциальных уравнений методом РунгеКутта 4го порядка
 Скачать 83.86 Kb. Скачать 83.86 Kb.
|
|
Абхазский государственный университет Физико-математический факультет КАФЕДРА «ПРИКЛАДНАЯ МАТЕМАТИКА И ИНФОРМАТИКА» Курсовая работа На тему: «Программная реализация решения системы обыкновенных дифференциальных уравнений методом Рунге-Кутта 4-го порядка» Выполнил студент III курса Евдокимов Т. Д. Научный руководитель Зантария З. Л. Сухум 2021 ОглавлениеВведение 2 Глава 1. Теоретическая часть 4 1.1 Обыкновенное дифференциальное уравнение первого порядка. Задача Коши 4 1.2 Суть метода Рунге-Кутта 4 1.3 Порядок вычислений по методу Рунге-Кутта 5 1.4 Свойства метода Рунге-Кутта 6 Глава 2. Практическая часть 6 2.1 Выбор среды разработки 6 2.2 Математическая реализация метода Рунге-Кутта 4-го порядка 7 2.3 Программная реализация метода Рунге-Кутта 4-го порядка 8 Заключение 9 ВведениеПри изучении самых разнообразных явлений окружающего мира, имеющих отношение как к точным, так и к гуманитарным наукам, исследователи сталкиваются в ряде случаев с тем, что функциональные зависимости между величинами находятся из уравнений, в которых присутствуют производные от искомых функций. Наиболее простыми среди них являются те, что содержат только производные первого порядка и могут быть записаны в виде 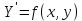 где у - искомая функция, х - независимая переменная, f(x,y) - непрерывная функция от х и у. Однако получить аналитическое решение этого уравнения для достаточно произвольной функции f не удается, и только для некоторых частных случаев, с которыми можно ознакомиться в справочной литературе. В связи с быстрым развитием электронной вычислительной техники в последние десятилетия появилась возможность использовать приближенные математические методы для решения подобного рода задач. Один из таких подходов называется методом Рунге-Кутты и объединяет целую группу модификаций, связанных способом их получения. Цель курсовой работы: изучить метод Рунге - Кутта 4-го порядка для решения обыкновенных дифференциальных уравнений. Постановка задачи: необходимо составить программу, позволяющую решать обыкновенные дифференциальные уравнения методом Рунге - Кутта 4-го порядка. Глава 1. Теоретическая часть1.1 Обыкновенное дифференциальное уравнение первого порядка. Задача КошиДля простоты рассмотрим двумерное пространство переменных х и у и некоторое открытое множество G, принадлежащее ему. Пусть на этом открытом множестве определена непрерывно дифференцируемая функция f(х, у) и задано уравнение 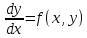 (1) (1)Согласно теореме существования и единственности для любой точки (x0,y0) ∈G найдется решение у = у(х), определенное на некотором интервале (х0 -δ, х0 +δ), удовлетворяющее условию y(x0) = y0, такое, что точки (x,y(x)) ∈G и y‘x ≡ f(x, y(x)), причем это решение будет единственным. Задача для уравнения (1) с начальным условием у(х0) = y0 (задача Коши) состоит в нахождении функции у(х), обращающей и уравнение (1), и начальное условие в тождество. Допустим, что значения, которые принимает независимое переменное х, принадлежат интервалу (Х0, XN ) и запишем задачу Коши: 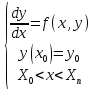 (2) (2)Разобьём отрезок [Х0, XN ] на N частей так, что 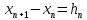 , ,n = 0, … ,N-1. В дальнейшем, не ограничивая общности, рассмотрим случай, когда разбиение равномерное, т.е. все 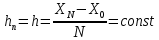 , n = 0 ,… ,N-1. , n = 0 ,… ,N-1.1.2 Суть метода Рунге-КуттаМетоды Рунге-Кутта находят широкое применение при решении ДУ. Наибольшее применение нашел метод 4-го порядка. При решении методом Рунге-Кутта дифференциального уравнения 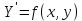 с начальными условиями с начальными условиями 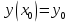 через через 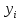 обозначают приближенное значение искомого решения в точке обозначают приближенное значение искомого решения в точке 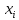 и вычисление приближенного значения и вычисление приближенного значения 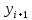 в следующей точке в следующей точке 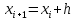 производится по формулам производится по формулам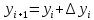 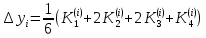 где 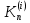 - параметр, который определяет значение функции вблизи точки - параметр, который определяет значение функции вблизи точки Общепринятый метод 4-го порядка: 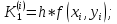 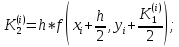 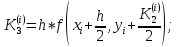 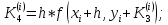 Этот метод намного более точен, чем методы Эйлера, но требует и большего объема вычислений: положение точки 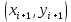 определяется в результате 4-кратного вычисления значения функции определяется в результате 4-кратного вычисления значения функции 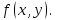 С появлением ЭВМ этот недостаток перестал быть существенным и метод Рунге-Кутта 4-го порядка применяется на практике чрезвычайно широко. С появлением ЭВМ этот недостаток перестал быть существенным и метод Рунге-Кутта 4-го порядка применяется на практике чрезвычайно широко.1.3 Порядок вычислений по методу Рунге-КуттаПорядок вычисление по методу Рунге-Кутта следующий: Выбираются 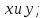 Вычисляются 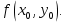 Определяются Определяются 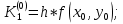 Определяются 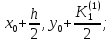 Вычисляются 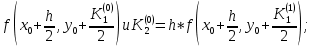 Принимаются 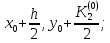 Вычисляются 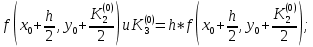 Определяются  Вычисляются 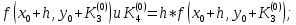 Суммируются 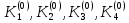 делим на 6 и получаем делим на 6 и получаем  Затем все вычисления продолжаются в том же порядке, принимая за начальную точку 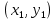 и т.д. и т.д.Схема метода Рунге-Кутта показана ниже
1.4 Свойства метода Рунге-КуттаМетод Рунге-Кутта обладает следующими свойствами: 1. Метод является одноступенчатым (чтобы найти . Не требует вычисления производных от 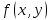 , а требует вычисления самой функции , а требует вычисления самой функции. Имеет небольшую погрешность Глава 2. Практическая часть2.1 Выбор среды разработкиДля выполнения поставленной задачи был выбран программный продукт DEV-C++ (или Microsoft Visual Studio). Так как является более простым в использовании и соответствует всем необходимым требованиям для создания консольного приложения.\ 2.2 Математическая реализация метода Рунге-Кутта 4-го порядкаРешить задачу Коши: 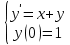 на отрезке [0: 0,4]. Найти решение на равномерной сетке с шагом 0.1 Решение. Так как 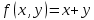 , то получаем , то получаемРешение: Так как 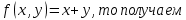 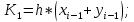 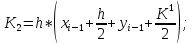 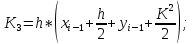 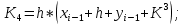 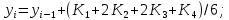 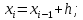 Для значений 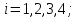 Полагая 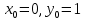 , последовательно находим: , последовательно находим:При i=1 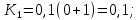  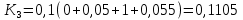 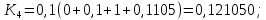 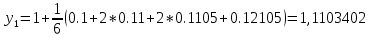  При i=2 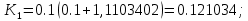 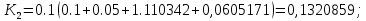 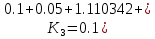 0,06604295) = 0.1326385; 0,06604295) = 0.1326385;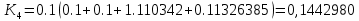 ; ;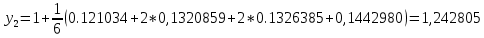 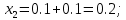 При i=3 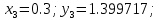 При i=4 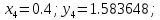 2.3 Программная реализация метода Рунге-Кутта 4-го порядкаDEV-C++  РЕЗУЛЬТАТ 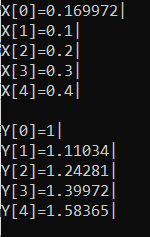 ЗаключениеМетоды Рунге — Кутты (в литературе встречается название методы Рунге — Кутта) — большой класс численных методов решения задачи Коши для обыкновенных дифференциальных уравнений и их систем. Первые методы данного класса были предложены около 1900 года немецкими математиками К. Рунге и М. В. Куттой. К классу методов Рунге — Кутты относятся явный метод Эйлера и модифицированный метод Эйлера с пересчётом, которые представляют собой соответственно методы первого и второго порядка точности. Существуют стандартные явные методы третьего порядка точности, не получившие широкого распространения. Наиболее часто используется и реализован в различных математических пакетах (Maple, MathCAD, Maxima) классический метод Рунге — Кутты, имеющий четвёртый порядок точности. В ходе выполнения курсовой работы была реализована поставленная задача, а именно составлена программа, позволяющая решать обыкновенные дифференциальные уравнения методом Рунге - Кутта 4-го порядка. |