РГР_Слєпцова_ДА-62. Програмна реалізація методу
 Скачать 145.82 Kb.
|
|
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ «КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ» ім. Ігоря Сікорського» Кафедра системного проектування (повна назва кафедри, циклової комісії) РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА з дисципліни "Теорія інформації і кодування" (назва дисципліни) на тему:________________Програмна реалізація методу_________________ ____________________ арифметичного кодування _______________________ Студентки ___ІІ___курсу групи___ДА-62__ _________________________Слєпцової О.О. (прізвище та ініціали) Керівник _______доц., к.т.н. __Капшук О.О. (посада, вчене звання, науковий ступінь, прізвище та ініціали) Київ-2018 ЗМІСТ 2.6 Ефективність кодування 9 Щоб визначити ступінь стиснення результати слід перевести в двійкову форму. З кінцевого інтервалу [0.71753375 0.717535) можна обрати будь-яке число. Наприклад, найменше для зберігання – 717534, якому відповідає бітове значення 1010 1111 0010 1101 1110, що складається з 20 біт. Вихідне повідомлення містило 10 символів, тобто займало 10 байт або 8∙10=80 біт. Отже, стиснута інформація займає в 4 рази менше місця.. 9 3. Аналіз існуючих алгоритмів реалізації методу 10 3.1 Класичний метод 10 3.2 Range-кодування 11 3.3 Адаптивне кодування 11 4.1 Вирішення проблеми точності 15 4.2 Використання адаптивного арифметичного кодування 15 5.1 Особливості реалізації 16 1. ВСТУП В наші дні інформація є головним інструментом у розвитку фундаментальних наук, технологій, методів роботи і навчання. За допомогою передачі інформації люди обмінюються досвідом, знаннями і корисними відомостями, що, безсумнівно, веде до прогресу у всіх областях людської діяльності. Обсяги електронної інформації, що передається, зростають з величезною швидкістю. Однак, незважаючи на високу пропускну здатність сучасних каналів зв'язку, передача великих обсягів інформації завжди пов'язана зі значними тимчасовими витратами. Саме тому виникла така область інформаційних технологій, як стиснення даних. Теорія стиснення даних об'єднує в собі кілька різних напрямків. У рамках даної теорії методи прийнято розділяти на методи кодування інформації без втрат (lossless) і методи кодування інформації з втратами (lossy). Як випливає з назв, методи першої групи не ведуть до інформаційних втрат, тоді як використання методів другої групи пов'язане з такими втратами. Застосування стиснення без втрат особливо важливо для текстової інформації, що записується на природних і на штучних мовах, оскільки в цьому випадку помилки зазвичай неприпустимі. У свою чергу стиснення з втратами застосовується до інформації, що містить окремі несуттєві складові, які за певних умов можуть бути частково або повністю вилучені. Методи стиснення з втратами часто використовуються для стиснення звуку і зображень. Арифметичне кодування, є одним з перспективних методів стиснення інформації, та, в певному розумінні, її шифрування. Це кодування дозволяє скоротити код символу вхідного алфавіту за умови, що розподіл частот цих символів відомий. Концепція методу була розроблена Еліасом в 60-х роках. Однак перші кроки в напрямку практичної реалізації даної ідеї були зроблені Паско в 1976 р. Арифметичне кодування є оптимальним, і його ефективність прямує до теоретичної межі ступеню стиснення – ентропії вхідного потоку. 2. ОПИС АЛГОРИТМУ Алгоритм арифметичного кодування є двопрохідним, тобто включає в себе етап аналізу вхідних даних та етап кодування, спираючись на отримані ймовірнісні інтервали кожного символу (байту). Вихідний файл складається з таблиці частот символів та десяткового дробу, що відповідає вхідному тексту. 2.1 Характеристики Забезпечує майже оптимальний степінь стиснення з точки зору ентропійної оцінки кодування Шеннона. На кожний символ необхідно майже H біт, де H – інформаційна ентропія джерела. На відміну від алгоритму Хаффмана, метод арифметичного кодування демонструє високу ефективність для дробних нерівномірних інтервалів розподілу ймовірностей символів, що кодуються. Але у випадку рівноймовірнісного розподілу символів, наприклад для рядку біт 010101...0101 довжини s метод арифметичного кодування наближується до префіксного коду Хаффмана і навіть може займати на один біт більше. 2.2 Принцип дії Нехай є деякий алфавіт, а також дані про частоту використання символів. Тоді розглянемо на координатній прямій відрізок від 0 до 1. Назвемо такий відрізок робочим. Розташуємо на ньому точки таким чином, що довжини утворених відрізків будуть рівними частоті використання символу і кожний такий відрізок буде відповідати одному символу. Потім візьмемо символ з потоку і знайдемо для нього відрізок серед щойно сформованих, тепер відрізок для цього символу став робочим. Розіб’ємо його таким же чином, як розбили інтервал  . Виконаємо цю операцію для деякого числа послідовних символів. Потім необхідно обрати нижню межу результуючого відрізка, що і є результатом роботи алгоритму для вхідної послідовності символів потоку.2.3 Реалізація алгоритму Ідею арифметичного кодування найкраще розглянути на простому прикладі. Наприклад, необхідно закодувати повідомлення Slieptsova_Olga_Olegovna. Табл. 2.3 – Ймовірності символів.
2.4 Кодування Кожному символу ставиться у відповідність ймовірність його появи (табл. 2.3). В арифметичному кодуванні кожен символ представлено інтервалом у діапазоні [0, 1), у відповідності з частотою його появи. В даному випадку буде отримано такий набір інтервалів: Табл. 2.4 – Кодування звичайним арифметичним кодуванням.
Процес моделювання починається зі зчитування першого символу вхідного потоку та надання йому інтервалу з начального діапазону [0, 1). В даному випадку для першого символу “O” діапазоном буде [0; 0,1666667). Далі, зчитується другий символ – “L ”, якому відповідає інтервал [0,1666667; 0,2916667). Але вихідний діапазон [0,1) вже скоротився до [0; 0,1666667), тому символ “L” слід представити в цьому новому інтервалі. Для цього достатньо визначити нові нижню та верхню межі. Дані межі можна розрахувати за формулами NewHigh = OldLow + (OldHigh-OldLow)∙HighRange(X), NewLow = OldLow + (OldHigh-OldLow)∙LowRange(X), де OldLow – нижня межа інтервалу, в якому представляється поточний символ; OldHigh – верхня межа інтервалу; HighRange(X) – вихідна верхня межа символу, який кодуємо; LowRange(X) – вихідна нижня межа символу, який кодуємо. Застосовуючи наведені формули для визначення меж символу символа “L”. Табл. 2.4.1 – Знаходження нових меж символа.
Кінцевий вихідний код – останнє значення змінної Low 0.586254899930338 Це і буде нашим вихідним кодом. 2.5 Декодування Відновлення інформації відбувається в протилежному порядку. 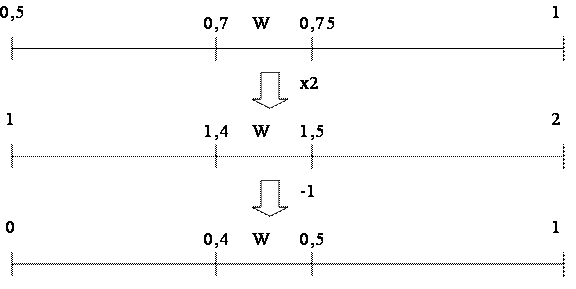 Рисунок 2.3 Схема відновлення вихідних інтервалів символа W Застосовуючи дану схему до числа 0,005510701012382210, отримуємо нижню межу наступного закодованого символу так, ніби він був початковим при кодуванні: Нормалізація виконується за формулою: Code = (Code-LowRange(X))/(HighRange(X)-LowRange(X)), де Code – поточне значення коду. Наприклад, користуючись цією формулою для коду, що в точності співпадає з попередньою схемою розрахунків. Аналогічно виконується декодування всіх символів строки. В табл.2.4 наведені коди, розраховані при декодуванні символів. Слід зазначити, що процес декодування в даному випадку можна зупинити, якщо значення коду рівне нулю. Проте це не завжди так. Бувають випадки, коли нуль містить в собі код наступного символу, а не означає кінець процедури декодування. Тут виникає проблема завершення декодування. Для цього й використовують спеціальний символ EOF, який сповіщає про те, що він останній і декодування можна припинити. При цьому частота цього символу очевидно повинна бути надзвичайно малою в порівнянні з частотою символів алфавіту послідовності, наприклад, можна виділити йому інтервал [0,999999 1). 2.6 Ефективність кодуванняЩоб визначити ступінь стиснення результати слід перевести в двійкову форму. З кінцевого інтервалу [0.71753375 0.717535) можна обрати будь-яке число. Наприклад, найменше для зберігання – 717534, якому відповідає бітове значення 1010 1111 0010 1101 1110, що складається з 20 біт. Вихідне повідомлення містило 10 символів, тобто займало 10 байт або 8∙10=80 біт. Отже, стиснута інформація займає в 4 рази менше місця..Можна перевірити оптимальність стиснення за ентропією: 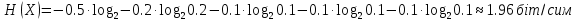 і складе 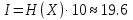 біт, що в цілих значеннях рівне 20 біт. Отже, отриманий код досяг мінімально можливого значення та є оптимальним. В загальному випадку можна показати, що за достатньо великої послідовності арифметичний кодер завжди показує оптимальні результати стиснення, тобто є найкращим серед ентропійних кодерів. |