РГР_Слєпцова_ДА-62. Програмна реалізація методу
 Скачать 145.82 Kb. Скачать 145.82 Kb.
|
3. Аналіз існуючих алгоритмів реалізації методуІснує кілька методів, які дозволяють реалізувати ідею арифметичного кодування, ось деякі з них: 3.1 Класичний методЦей метод заснований на ідеї присвоювання коду всьому, зазвичай, великому файлу, що передається, замість кодування окремих символів. Вхідним файлом може бути текст, зображення або дані любого виду. Алгоритм зчитує файл символ за символом та додає біти до зжатого файлу. Щоб зрозуміти метод, корисно уявити отриманий код у вигляді числа з напівінтервалу 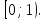 Тут Тут 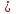 позначає числа від a до b, включаючи a та виключаючи b. Таким чином код 9746509 необхідно інтерпретувати як число позначає числа від a до b, включаючи a та виключаючи b. Таким чином код 9746509 необхідно інтерпретувати як число 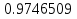 , але частина 0. не буде передана у вихідний файл. Використання такого коду дає можливість однозначно відновити послідовність символів, з яких він був побудований. На першому етапі необхідно визначити частоту появи кожного символу алфавіту. Найкращого результату можна досягти, зчитавши весь вхідний файл на першому проході алгоритму стиснення ,що складається з двох проходів. Але, якщо програма може отримати оцінку частот символів з іншого джерела, перший прохід можна відкинути [10]. , але частина 0. не буде передана у вихідний файл. Використання такого коду дає можливість однозначно відновити послідовність символів, з яких він був побудований. На першому етапі необхідно визначити частоту появи кожного символу алфавіту. Найкращого результату можна досягти, зчитавши весь вхідний файл на першому проході алгоритму стиснення ,що складається з двох проходів. Але, якщо програма може отримати оцінку частот символів з іншого джерела, перший прохід можна відкинути [10].Ідея арифметичного кодування полягає в таких кроках:
Межі підінтервалів 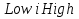 для кожного символу визначаються за формулами: для кожного символу визначаються за формулами: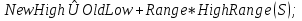 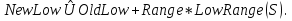 Де 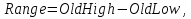 а а 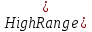 S) і S) і 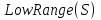 визначають верхній і нижній кінець області символу s. Коли всі символи опрацьовано, отримаємо кінцевий інтервал, нижня межа якого і є шуканим кодом. визначають верхній і нижній кінець області символу s. Коли всі символи опрацьовано, отримаємо кінцевий інтервал, нижня межа якого і є шуканим кодом.3.2 Range-кодуванняВ даному різновиді алгоритму кодування особливих відмінностей від стандартної реалізації немає. Тільки поточний інтервал представляється не верхньою і нижньою межею, а нижньою межею та шириною. Працює кодер точно так само, проте дана методика дозволяє значно прискорити виконання, так як ширина інтервалу не розраховується окремо і можна відразу перевірити чи потрапила вона в межі, допустимі для розширення чи ні. 3.3 Адаптивне кодуванняДля арифметичного кодування існує також адаптивний алгоритм, тобто алгоритм, що при кожному співставленні символу коду, окрім того, змінює внутрішній код обчислень так, що наступного разу цьому ж символу може бути наданий інший код, тобто відбувається “адаптація” алгоритму до символів, що надходять. При декодуванні відбувається аналогічний процес. 3.3.1 Особливості алгоритму Кожному символу ставиться у відповідність його вага, спочатку вага для всіх рівна 1. Всі символи розташовуються в природному порядку, наприклад, за зростанням. Ймовірність кожного символу встановлюється рівною його вазі, поділеній на сумарну вагу всіх символів. Після отримання наступного символу та побудови інтервалу для нього, вага цього символу збільшується на 1. Для того, щоб забезпечити зупинку алгоритму розпаковки, на початку стиснутого повідомлення слід поставити його довжину, або ввести додатковий символ маркер. Потім, методом аналогічним простому арифметичному кодуванню, обирається число, що описує кодування. Декодування відбувається наступним чином: на кожному кроці визначається інтервал, що містить даний код(обране число) – за цим інтервалом однозначно задається вихідний символ повідомлення. Потім з поточного коду віднімається нижня межа інтервалу, що містить даний символ, отримана різниця ділиться на довжину цього ж інтервалу. Отримане число вважається новим поточним значенням коду. Задана множина символів – це, зазвичай, ASCII+. Для того, щоб забезпечити зупинку алгоритму розпаковки на початку повідомлення, яке стискають, слід поставити його довжину, або ввести додатковий символ-маркер кінця повідомлення. Якщо знати формат файлу для стиснення, то замість початкового рівномірного розподілу ваги можна обрати розподіл з врахуванням цих знань. Наприклад, в текстовому файлі є низка недопустимих символів і їх вагу можна занулити. 3.3.2 Кодування Вхідне повідомлення: “ABBACD” На першому кроці вага всіх символів – 1. Поточний інтервал [0, 1]. Першим кодується символ А. Оскільки символів 4, і їх вага однакова, то береться чверть від вихідного відрізку. Утворюється інтервал [0, 0.25]. Символ А оброблено, його вага збільшується на одиницю. Загальна вага також збільшується на одиницю. Наступним кодується символ В. Поточний інтервал розбивається відповідно до відношення ваги символів до сумарної ваги. Обирається інтервал, що відповідає символу В – [1/10, 3/20]. Вага символу В збільшується на одиницю. Подібним чином кодування виконується далі. Всі кроки наведено в табл..3.2
1979/16384 = 1979/214, звідси виходить, що вихідне повідомлення можна представити у вигляді двійкового числа 0.000111101110112 є [1826/15120, 1827/15120]. Таким чином, повідомлення було закодоване за допомогою 14 бітів. ML = 2.3 біт/сим. 3.3.3 Декодування Код 00011110111011 можна розкодувати, знаючи множину символів, з яких складалось вихідне повідомлення. Отже, 000111101110112 = 1979/16384. Результати розрахунків наведено в таблиці.:
4. Обґрунтування вибору алгоритмів компресії та декомпресії | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
