математика. 14 задание. Производная функции
 Скачать 188.33 Kb. Скачать 188.33 Kb.
|
|
Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Производная и её применение:Последовательность Понятие предела последовательности имеет простую геометрическую интерпретацию Неравенство вида Это означает, что если Последовательность, не имеющую предела, называют расходящейся. Например, последовательность  Расходящейся является и последовательность Тогда для 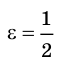 вне интервала вне интервала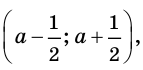 длина которого равна длина которого равна 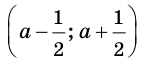 не может содержать числа не может содержать числа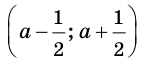 находится бесконечное количество членов последовательности: или находится бесконечное количество членов последовательности: или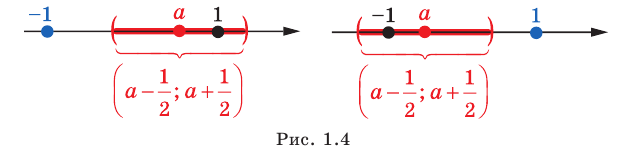 Следовательно, Находить пределы числовых последовательностей помогает следующая теорема. Теорема 1.1 (об арифметических действиях с пределами последовательностей). Если последовательности 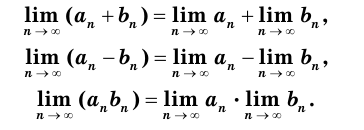 Пример:Найдите 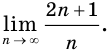 Решение: Имеем: 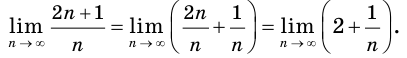 Последовательность с общим членом 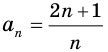 представлена в виде суммы двух сходящихся последовательностей с общими членами представлена в виде суммы двух сходящихся последовательностей с общими членами 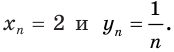 Тогда можно записать: Тогда можно записать: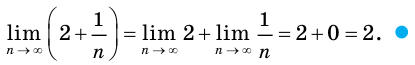 Пример №3Вычислите предел 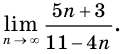 Решение: Разделим числитель и знаменатель дроби 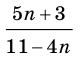 на на 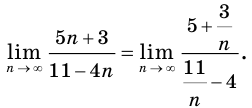 В числителе и знаменателе полученной дроби записаны общие члены сходящихся последовательностей. Тогда: 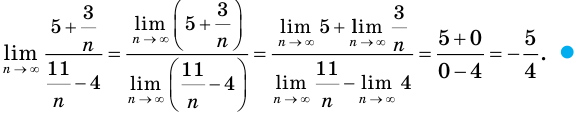 Тригонометрические функции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе. Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций разнообразны. Например, любые процессы можно представить в виде суммы тригонометрических функций. Данные функции появляются при решении дифференциальных и функциональных уравнений. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На рисунке изображен круг радиусом r = 1. На окружности обозначена точка M (x, y). Угол между радиус-вектором OM и направлением оси Ox равен a. 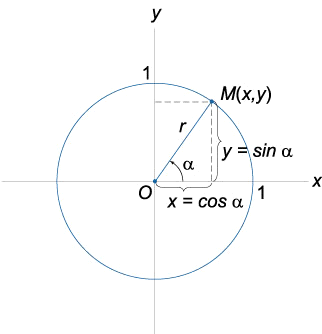 Синусом угла α называется отношение ординаты y точки M (x, y) к радиусу r: sin α = y/r. Поскольку r = 1, то синус равен ординате точки M (x ,y). Косинусом угла α называется отношение абсциссы x точки M (x,y) к радиусу r: cos α = x/r = x. Тангенсом угла α называется отношение ординаты y точки M (x, y) к ee абсциссе x: tg α = y/x, x ≠ 0. Котангенсом угла α называется отношение абсциссы x точки M (x, y) к ее ординате y: ctg α = x/y, y ≠ 0. В единичном круге x, y точки M (x, y) и радиус r образуют прямоугольный треугольник, в котором x, y являются катетами, а r − гипотенузой. Поэтому, определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: -Синусом угла α называется отношение противолежащего катета к гипотенузе. -Косинусом угла α называется отношение прилежащего катета к гипотенузе. -Тангенсом угла α называется отношение противолежащего катета к прилежащему. -Котангенсом угла α называется отношение прилежащего катета к противолежащему. К тригонометрическим функциям относятся, во-первых, прямые тригонометрические функции: синус (sin x), косинус (cos x); во-вторых, противоположные им тригонометрические функции: секанс (sec x) косеканс (cosec x); и, в-третьих, производные тригонометрические функции: тангенс (tg x), котангенс (ctg x). Каждому действительному числу x соответствует единственная точка единичной окружности, получаемая поворотом точки (1;0) на угол x радиан. Для этого угла определены sin x и cos x. Каждому действительному числу x поставлены в соответствие числа sin x и cos x, т.е. на множестве R всех действительных чисел определены функции y = sin x и y = cos x. Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел. Функция y = tg x определяется формулой y = tg x = sin x/cos x. Эта функция определена при тех значениях x, для которых cos x ≠ 0. Известно, что cos x = 0 при x = π/2 + πn, n Є Z. Следовательно, областью определения функции y = tg x является множество чисел x ≠ π/2 + πn, n Є Z. Так как уравнение tg x = a имеет корни при любом действительном значении a, то множеством значений функции y = tg x является множество R всех действительных чисел. Пример 1: Решим уравнение: a) sin x = 1/2 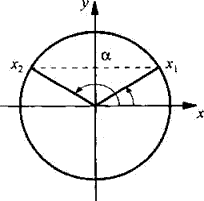 а) На оси ординат отложим значение 1/2 и построим углы x1 и х2, для которых sin x = 1/2. При этом х1 + х2 = π, откуда х2 = π – x1. По таблице тригонометрических функций найдем величину х1 = π/6, тогда Скажем периодичность функции синуса и запишем решения данного уравнения: Пример 2: Найдем: Учитывая обратные тригонометрические функции получим: 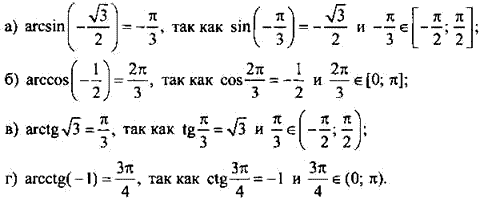 |
