курсовая по подвескам. курсач по проектировании. Простая контактная подвеска

• Название: Простая контактная подвеска
• Анкор: курсовая по подвескам
• Дата: 03.12.2021
• Размер: 484.86 Kb.
• Имя файла: курсач по проектировании.docx
• Тип: Документы; #290546
• страница: 4 из 4

Расчет двойной цепной подвески. Натяжения и стрелы провеса несущего троса двойной цепной подвески определяются по уравнению (3.92), причем величина К в выражениях Z и W, входящих в это уравнение, принимается равной сумме натяжений вспомогательного и контактных проводов при соответствующих значениях температуры.

При определении значения коэффициента φ для схемы двойной подвески (рис. 3.33), величина с берется равной а.

В том случае, если вспомогательный провод не компенсирован, величины его натяжений и стрел провеса в зависимости от температуры определяются предварительно отдельным расчетом.

Вспомогательный провод рассчитывается как гибкая пить, подверженная действию двух равных сосредоточенных нагрузок (рис. 3.34), значения которых определяются выражениями:

при двух контактных проводах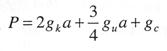



при одном контактном проводе



где g_к — масса 1 пог. м контактного провода;

       g_u – масса 1 пог. м вспомогательного провода;

       g_c — масса между вспомогательным и контактным проводами;

       а — расстояние между струнами контактных проводов.

 



Рис. 3.33. Схема двойной цепной подвески: 1 — вспомогательный трос; 2 — контактный провод;  3 — струна; 4 — несущий трос

 



Рис. 3.34. Схема для расчета вспомогательного провода двойной цепной подвески

 

Обозначим:

U_x и U₁ — натяжение вспомогательного провода при определяемом и исходном режимах;

ψ_х и ψ₁ — стрелы провеса вспомогательного провода при определяемом и исходном режимах;

t_x и t₁ – температура определяемого и исходного режимов;

α_u, E_u, S_u — температурный коэффициент линейного расширения, модуль упругости и сечение вспомогательного провода.

Величина удлинения ΔL вспомогательного провода в пролете длиной l=2а при изменении натяжения провода на (U_x — U₁) и температуры на (t_x — t₁) определяется по выражению:

                                    (3.121)

То же удлинение вспомогательного провода можно определить из геометрических соотношений в зависимости от изменения стрелы провеса ψ.

Полная длина провода при стреле провеса ψ_х определяется (см. рис. 3.34) по выражению

                                  (3.122)

Приравнивая нулю сумму моментов сил, приложенных влево от точки А (точки приложения сосредоточенной силы Р_х), получим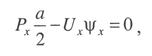



откуда

                                             (3.123)

Подставляя полученное значение ψ_х в выражение (3.122), получим



откуда

                                    (3.124)

Заменяя корень в выражении (3.124) его приближенным значением



получим

                      (3.125)

Таким же образом получим значение длины провода L₁ при стреле провеса ψ₁ и натяжении U₁:

                                      (3.126)

Удлинение провода ΔL определится разностью выражений (3.125) и (3.126):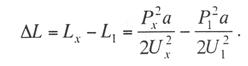

                            (3.127)

Приравнивая правые части выражений (3.121) и (3.127) и сокращая на 2а, получим



Это уравнение может быть приведено к виду



Отсюда, задаваясь значением U₁ — натяжением вспомогательного провода при исходном режиме t₁, можем определить зависимость U_x=f(t_x).

Значения стрел провеса ψ_x вспомогательного провода определяются из выражения (3.123).

Изменения высоты контактных проводов в середине пролета при двойной цепной подвеске находят по формуле

                                     (3.129)

а изменения под ближайшей от опоры струной цепной подвески — по формуле

                           (3.130)

где F_x и F₀ — стрелы провеса несущего троса;

       ψ_x и ψ₀ — стрелы провеса вспомогательного провода при определяемом режиме и при режиме расчетного беспровесного положения контактных проводов;

       φ_x — конструктивный коэффициент цепной подвески, определяемый по формуле (3.94).

Изменения высоты контактных проводов под опорой Δh_Bx могут быть приняты равными Δh_Ax.

В том случае, если вспомогательный провод компенсирован, следовательно



выражения (3.129) и (3.130) принимают вид



В заключение следует отметить, что методы расчетов цепных подвесок (натяжений, стрел провеса) продолжают совершенствоваться как в России, так и за рубежом. Расчеты для полностью компенсированных подвесок значительно упрощаются. Конечное число струн (между первыми нерессорными) учитывается в методиках Уральского государственного университета путей сообщения (А.В. Ефимов, А.Г. Галкин). Широко используются возможности расчета на ЭВМ.