курсовая по подвескам. курсач по проектировании. Простая контактная подвеска
 Скачать 484.86 Kb. Скачать 484.86 Kb.
|
|
Критическая нагрузка и эквивалентный пролет цепной подвески. Исходным расчетным режимом для цепной подвески, т. е. тем режимом, при котором натяжение в несущем тросе получается наибольшим, может быть или режим наинизшей температуры, или режим наибольшей дополнительной нагрузки. Установить, какой из двух режимов следует принять за исходный, можно посредством определения критической нагрузки, которой называют такую результирующую нагрузку, когда натяжение несущего троса равно наибольшему допустимому его значению и при минимальной температуре, и при наибольшей дополнительной нагрузке. Если значение результирующей нагрузки при наибольшей дополнительной нагрузке от гололеда и ветра больше критической нагрузки, то исходным будет режим наибольшей дополнительной нагрузки (гололедный режим), в противном случае исходным будет режим наинизшей температуры. Значение критической нагрузки qx для расчетного пролета l определяется из уравнения (3.91), если данные с индексом «х» отнести к гололедному режиму, а с индексом «1» — к режиму наинизшей температуры. Так как в данном случае согласно определению понятия «критическая нагрузка» Тг = Tmin = Tmax, то уравнение (3.91) примет вид: 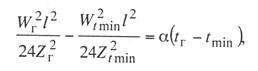 (3.100) (3.100)где 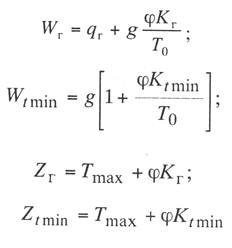 Определив из этого уравнения значение критической нагрузки qк, получим 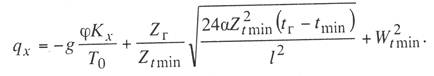 (3.101) (3.101)Для полукомпенсированной цепной подвески при К= соnst: поэтому выражение (3.101) принимает вид 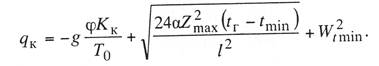 (3.102) (3.102)При определении значения gк по формуле (3.102) можно принять Для длин пролетов, применяемых в контактных сетях железных дорог, с достаточной степенью точности можно считать: — при медном несущем тросе Т0=0,75 Тmах; — при стальном и биметаллическом сталемедном несущем тросе Т0 = 0,8Тmax. При этом ошибка в определении значения критической нагрузки не превосходит ±2%, что вполне достаточно для практичес ких расчетов. Для определения величины эквивалентного пролета некомпенсированной или полукомпенсированной цепной подвески применимы те же рассуждения которые были приведены для простой подвески. Удлинение несущего троса в пролете длиной li при переходе от режима с индексом «1» к режиму с индексом «х» согласно выражениям (3.89) и (3.90) получится равным 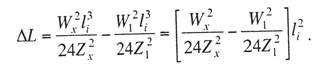 Принимая, что конструктивный коэффициент цепной подвески φ, а следовательно, и значения приведенной нагрузки Wx и W1 остаются одними и теми же во всех пролетах анкерного участка, и суммируя удлинения ΔL во всех пролетах, получим уравнение 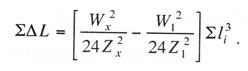 Разделив это выражение на 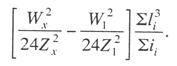 Приравнивая это относительное удлинение к сумме упругого и температурного относительных удлинений несущего троса, будем иметь 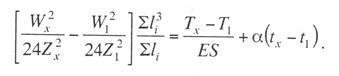 (3.103) (3.103)Так как в эквивалентном пролете согласно его определению значения натяжений несущего троса должны изменяться по тому же закону, что и на рассматриваемом анкерном участке, то для эквивалентного пролета lэ может быть написано следующее уравнение: 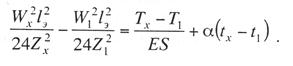 (3.104) (3.104)Приравнивая левые части выражений (3.103) и (3.104), получим 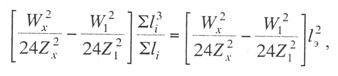 откуда 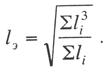 (3.105) (3.105)Таким образом, для цепной подвески, имеющей однотипную конструкцию во всех пролетах анкерного участка, величина эквивалентного пролета определяется той же формулой, что и для свободно подвешенного провода. В тех случаях, когда величины пролетов анкерного участка не значительно отличаются друг от друга, эквивалентный пролет, определяемый по формуле (3.105), получается близким к среднему арифметическому значению пролета для данного анкерного участка и без ущерба для точности расчета может быть заменен этим значением. Расчет натяжения несущего ненагруженного троса. Кроме значений натяжения несущего троса цепной подвески в нагруженном его состоянии иногда бывает необходимо знать также величины натяжений ненагруженного несущего троса, т. е. значения тех натяжений, которые должен иметь несущий трос при его монтаже до подвески на нем контактных проводов. Натяжение ненагруженного несущего троса можно определить по формуле простой подвески, приняв в качестве исходного режима режим загрузки несущего троса контактными проводами при температуре t0 и беспровесном их положении. Для этого обозначим: Т0 — натяжение нагруженного несущего троса при температуре t0 беспровесного положения контактных проводов, м; Hx — определяемое натяжение ненагруженного троса при температуре tx; g0 — нагрузка от собственного веса цепной подвески; gт — нагрузка от собственного веса несущего троса. После подстановки этих значений получим 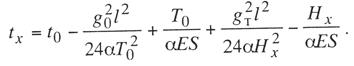 (3.106) (3.106)Подставляя в полученное уравнение различные значения Нх, взятые через произвольные интервалы, определяем соответствующие значения tx и строим кривую Нx =f(tx). Соответствующие величины стрел провеса вычисляют по формуле 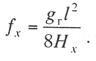 (3.107) (3.107)Если при монтаже цепной подвески подвешивают только один контактный провод, но в дальнейшем предусматривается возможность подвески второго, то сначала определяют натяжение несущего троса с двумя контактными проводами по формуле (3.106), а затем рассчитывают его натяжение при одном контактном проводе в режиме беспровесного положения контактных проводов. Обозначим: Т01 – натяжение несущего троса при одном контактном проводе при температуре беспровесного положения контактного провода; Т02 — натяжение несущего троса, нагруженного двумя контактными проводами, при температуре беспровесного положения контактных проводов; g1 — нагрузка от собственного веса цепной подвески при одном контактном проводе. g2 — нагрузка от собственного веса цепной подвески при двух контактных проводах; Тогда, применяя формулу простой подвески (3.4 1), можно написать 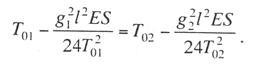 (3.108) (3.108)Определив из полученного выражения Т01, можно найти зависимость Тх=f(tx) для подвески с одним контактным проводом, пользуясь формулой (3.92) и принимая в качестве исходного режим беспровесного положения контактного провода. После введения принятых обозначений уравнение (3.92) получит вид: 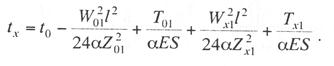 Подставив вместо W01 и Z01 их значения 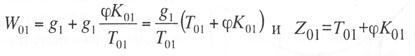 и сократив числитель и знаменатель второго члена в квадратных скобках на Т01+φК01, получим 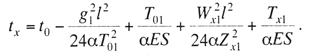 (3.109) (3.109)После определения значений Tx1 величины стрел провеса несущего троса с одним контактным проводом могут быть определены по формуле 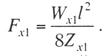 (3.110) (3.110)Расчет стрел провеса и изменений высоты контактных проводов и определение длин струн цепной подвески. Стрелы провеса fx контактных проводов цепной подвески определяются по формуле где Fx и F0 – стрелы провеса несущего троса в рассматриваемом пролете при расчетном режиме и при температуре расчетного беспровесного положения контактных проводов; φх – конструктивный коэффициент цепной подвески, определяемый по формуле (3.94). Изменения высоты контактных проводов одинарной цепной подвески в середине рассматриваемого пролета рассчитывают по формуле а под ближайшей от опоры простой (нерессорной) струной – из выражения Определение длин струн производим для общего случая, когда высота цепной подвески у опор, ограничивающих данный пролет, различны (рис. 3.31). 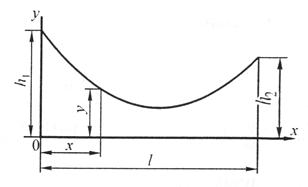 Рис. 3.31. Схема для расчета длины струны цепной подвески Рассмотрим цепную подвеску при режиме беспровесного положения контактных проводов. Принимая, что несущий трос располагается по параболе, ось абсцисс совпадает с контактным проводом, а ось ординат – с осью левой опоры, получим уравнение несущего троса в виде 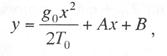 (3.114) (3.114)где y=h – высота искомой струны. Значение свободного члена В определяем из условия, что при х = 0 y=h1. Тогда 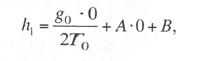 следовательно Значение коэффициента А можно определить из условия, что при х = l, у = h2. Тогда 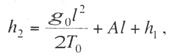 откуда 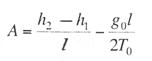 и уравнение (3.114) примет вид: 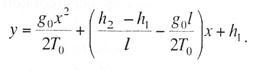 (3.115) (3.115)При h1 – h2 уравнение получит вид 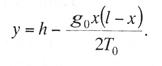 (3.116) (3.116)В этом случае пролет получается симметричным относительно его середины, и струны, находящиеся на одинаковых расстояниях от опор, получаются равными. Для определения минимальной длины нескользящей струны длиной С, находящейся на расстоянии L от средней анкеровки, угол наклона к вертикали определяется из выражения 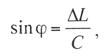 где ΔL — продольное смещение нижнего конца струны от среднего положения. Нескользящие струны могут применяться при угле наклона φ не более 300, в этом случае Sinφ=0,5 и выражение примет вид где Сmin — минимальная длина нескользящей струны; (ΔL)mах – наибольшая величина температурного смещения контактного провода в точке, расположенной на расстоянии L от средней анкеровки. Величина (ΔL)mах может быть определена приблизительно (без учета влияния изменений упругих деформаций контактного провода и перемещений, вызываемых изменениями стрел его провеса) из выражения где (Δt)max – наибольшая величина изменения температуры, (среднего ее значения); αк — коэффициент температурного расширения материала контактного провода. Подставляя значение (ΔL)mах в выражение для Сmin, получим Расчет рессорной цепной подвески. Определение натяжений и стрел провеса несущего троса рессорной цепной подвески производится по общим формулам (3.91) и (3.92). Определение изменений высоты контактных проводов в середине пролета и у ближайших от опор нерессорных струн производится по формулам (3.112) и (3.113). Таким образом, при расчете рессорной цепной подвески не обходимо дополнительно выяснить лишь изменения, происходящие в опорном узле цепной подвески, которые определяются принятыми параметрами рессорного провода. Рассмотрим опорный узел рессорной цепной подвески (рис. 3.32), где сплошными линиями показано положение проводов при температуре t0 и штриховыми — при температуре tx. Стрела провеса несущего троса в точке крепления к нему рессорного провода при температуре t0 определяется выражением: 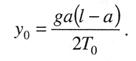 Для расчета стрелы провеса ψ0 рессорного провода при температуре t0 примем длину вертикальной части рессорной струны С не менее принятой минимальной длины струны Сmin. Отсюда получим (см. рис. 3.32) 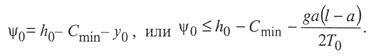 (3.117) (3.117)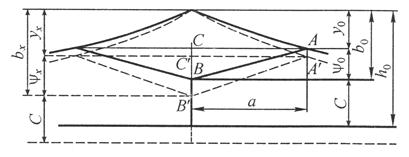 Рис. 3.32. Схема изменения положения проводов в подопорном узле рессорной цепной подвески: 1 — несущий трос; 2 — рессорный трос; З — рессорная струна; 4— контактный провод Расстояние b0 от точки крепления несущего троса у опоры до нижней точки рессорного провода определяется из выражения b0= у0+ψ0. При изменении температуры величины y0, ψ0 и b0 изменяются и получают при температуре tx значения yx, ψx и bx. Величина yx определяется на основании результатов расчета натяжения несущего троса по формуле 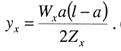 (3.118) (3.118)Значения ψx определяются отдельным расчетом, учитывая изменения длины ветвей рессорного провода, вызванные изменением температуры. При этом для упрощения расчета упругими изменениями длины рессорного провода пренебрегаем вследствие малого его натяжения и, кроме того, полагаем, что точки А и А’ находятся на одной вертикали. Длину ветви АВ рессорного провода при температуре t0 находим из треугольника АВС: При изменении температуры на величину (tx — t0) ветвь АВ займет положение А’В’, причем длина ее будет равна Зная величину А’В’, определим из треугольника А/ В/ С/ величину ψx 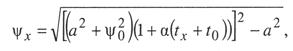 откуда, принимая после преобразования получим Зная ух и ψx можем определить изменения высоты контактных проводов под опорой по формуле Как видно из полученных формул (3.118) – (3.120), для определения значений ух, ψх и bx необходимо предварительно определить параметры рессорной струны: ψ0 – стрелу провеса рессорного провода при температуре t0 и а расстояние от опоры до точки закрепления рессорного провода на несущем тросе. Величина ψ0 ограничивается габаритными условиями цепной подвески и рассчитывается по формуле (3.117). Значения аи φ могут быть определены путем ряда пробных подсчетов при условии, что изменения высоты контактного провода под опорой при крайних температурных режимах должны получаться примерно такими же, как под ближайшими от опор простыми струнами, и что значения эластичности контактной подвески под опорами и под ближайшими от них простыми струнами будут примерно одинаковыми. |
