курсовая по подвескам. курсач по проектировании. Простая контактная подвеска
 Скачать 484.86 Kb. Скачать 484.86 Kb.
|
|
с простыми опорными струнами, когда струны устанавливают не далее 1—2 м от опор; со смещенными простыми опорными струнами, когда струны удалены от опор более чем на 2 м; в одинарной подвеске опорные простые струны устанавливают обычно на расстоянии 4—5 м от опоры, в двойной подвеске — на расстоянии 5—9 м; рессорной, в ней струны контактного провода (или вспомогательного провода — в двойных подвесках) закреплены на рессорном проводе; с упругими струнами, когда струны подвешивают к несущему тросу с помощью упругих элементов, например гибких полимерных стержней или рычагов, скручивающих несущий трос; демпфированной, в ее струнах у опор установлены демпферы. С целью унификации всех конструктивных размеров цепных подвесок с учетом применения типовых железобетонных опор контактной сети в типовых проектах конструктивную высоту цепных подвесок постоянного тока (с медным или сталеалюминевым несущим тросом и одним или двумя контактными проводами) принимают равной 2 м, цепных подвесок переменного тока (со сталемедным или сталеалюминевым несущим тросом и одним контактным проводом) в среднем 1,8 м. В компенсированной цепной подвеске при изменениях температуры воздуха происходит перемещение вдоль анкерного участка как контактного провода, так и несущего троса. Причем в случае изготовления троса и провода из одного материала эти перемещения будут одинаковыми, и, следовательно, при любых температурах струны подвески будут располагаться в ее плоскости вертикально, а если трос и провод из разнородных материалов, то с незначительным наклоном. Это позволяет выполнять компенсированную цепную подвеску с меньшей конструктивной высотой. Важным параметром цепной подвески является длина струнового пролета (см. рис. 5.3). Исследованиями установлено, что при больших струновых пролетах (более 12 м) из-за наличия местной стрелы провеса контактный провод в средней части струнового пролета изнашивается быстрее, чем у струн. Следовательно, чтобы износ контактного провода в пределах струновых пролетов был равномерным, необходимо их длины принимать по возможности меньшими, особенно в средней части пролета цепной подвески. В типовой компенсированной подвеске с одним контактным проводом в зависимости от длины пролета расстояние между струнами принимают 6—8 м, в подвеске с двумя контактными проводами 3,7-4,2 м (по несущему тросу при шахматном расположении струн). Двойные контактные провода в полукомпенсированной подвеске обычно крепят на общих струнах с отдельными нижними звеньями длиной по 300 мм для каждого провода с расстоянием между струнами не более 12 м. При электрификации железных дорог широкое применение находит компенсированная подвеска. По своим динамическим качествам она значительно превосходит полукомпенсированную. Даже при невысоких скоростях движения неравномерность нажатий полозов токоприемников на контактные провода при полукомпенсированной подвеске оказывается значительно выше, чем при компенсированной. Это приводит к неравномерному износу контактных проводов и повышению их среднего удельного износа, а следовательно, и уменьшению срока службы. Срок службы двойного контактного провода в компенсированной подвеске в 1,3 раза больше, чем в полукомпенсированной. На электрифицированных железных дорогах Казахстана смонтирована главным образом одинарная полукомпенсированная и компенсированная цепные подвески. Расчет цепных контактных подвесок Расчет натяжений и стрел провеса несущего троса.Особенностью механического расчета несущего троса цепной подвески является то, что кроме нагрузок от собственного веса и временных на грузок на него от гололеда и ветра он воспринимает также дополнительные нагрузки от веса контактных и вспомогательных проводов, а также от действия гололеда и ветра на эти провода. Величина этих дополнительных нагрузок колеблется в зависимости от изменения стрел провеса и натяжения контактных проводов, и только при беспровесном положении контактных проводов она равна сумме внешних нагрузок на отдельные провода подвески. В различных системах цепной подвески натяжения несущего троса изменяются по различным законам в зависимости от характера изменений стрел провеса контактных проводов той или иной системной подвески. При выводе уравнения состояния цепных подвесок принимается, что нагрузки от контактного и вспомогательного проводов, а также от струн и деталей подвески распределяются равномерно по длине несущего троса; при этом концы контактных проводов жестко закреплены. Это дает возможность получить уравнение в общем виде, откуда потом легко могут быть получены расчетные формулы для любого типа цепной подвески. Для вывода уравнения состояния цепной подвески принимаются следующие обозначения: l — длина пролета, м; g — нагрузка от веса проводов цепной подвески, кг/пог. м; q — результирующая нагрузка несущего троса, кг/пог. м; Т — горизонтальная составляющая натяжения несущего троса, кг; К — сумма натяжений контактных проводов (в двойной цепной подвеске также и вспомогательного провода), кг; F — стрела провеса несущего троса, м; fк — стрела провеса контактных проводов, м; Е — модуль упругости несущего троса, кг/мм S — сечение несущего троса, мм2; α — температурный коэффициент линейного расширения материала несущего троса; t — температура окружающего воздуха, °С. Величины Т, К, F, q и t с индексом «1» относятся к исходному режиму, с индексом «х» – к определяемому режиму и с индексом «0» — к режиму беспровесного положения контактного провода. Рассмотрим условия равновесия половины пролета цепной подвески (рис. 3.29). Пусть несущий трос имеет произвольную стрелу провеса F, не равную стреле провеса троса F0 при беспровесном положении контактного провода. Контактный провод получит при этом стрелу провеса fк. Обозначим отношение fк/(F— F0) через φ и назовем его конструктивным коэффициентом цепной подвески, тогда 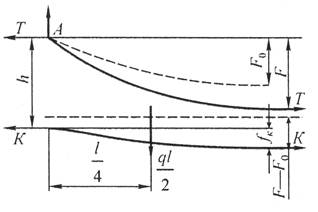 Рис. 3.29. Схема для расчета натяжений несущего троса цепной подвески Приравнивая к нулю сумму моментов всех сил относительно точки А, получаем 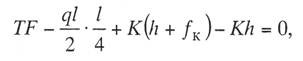 откуда после приведения подобных членов и замены fк его выражением (3.83) находим 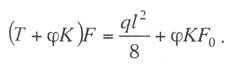 (3.84) (3.84)Так как при беспровесном положении контактного провода несущий трос можно рассматривать как свободно подвешенный провод, находящийся под действием нагрузки от собственной массы проводов цепной подвески, то значение F0 можем определить по формуле 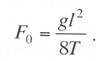 (3.85) (3.85)Подставив это значение F0 в уравнение (3.84), получим: 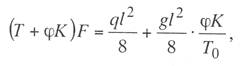 откуда 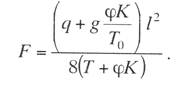 (3.86) (3.86)Обозначим 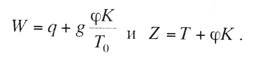 (3.87) (3.87)Тогда выражение стрелы провеса несущего троса примет вид 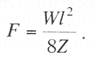 (3.89) (3.89)Величину W, имеющую размерность кг/пог. м, будем называть приведенной нагрузкой цепной подвески, величину Z — соответственно приведенным натяжением (при φ = 1 величина Z равна сумме натяжений всех проводов цепной подвески). Введение этих подстановок позволяет значительно упростить расчетные формулы цепной подвески и привести их к виду, подобному расчетным формулам простой подвески. Для вывода зависимости натяжения несущего троса от температуры и нагрузки определим значения удлинений несущего троса при переходе от одного режима температуры и нагрузки к другому. Пусть известно, что при температуре t1 и нагрузке q1 несущий трос имеет натяжение Т1 и стрелу провеса F1. Обозначим через Tx и Fx натяжение и стрелу провеса несущего троса при изменившихся температуре tx и нагрузке qx. При изменении стрелы провеса троса от значения F1 до значения Fx величину полного удлинения троса в пролете l можем определить согласно (3.23) через 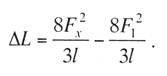 (3.90) (3.90)Так как полное удлинение троса составляется из упругого и температурного удлинений, можем приравнять выражение (3.90) сумме этих удлинений и получить уравнение 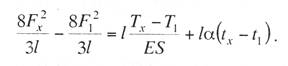 Заменив в этом уравнении Fx и F1 их значениями из выражения (3.89) и разделив обе части уравнения на l, находим 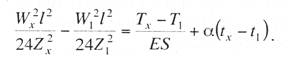 (3.91) (3.91)Левая часть этого уравнения представляет собой полное относительное удлинение несущего троса при переходе от одного режима температуры и нагрузки к другому, правая – сумму соответствующих упругого и температурного относительных удлинений. Величины W и Z в этом уравнении имеют следующие значения: 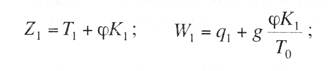 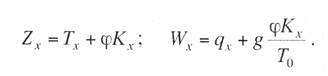 В случае полукомпенсированной цепной подвески К = соnst, вследствие чего Тx-T1 = Zx-Z1 и уравнение (3.91) принимает вид, полностью подобный уравнению для расчета простой подвески. Для решения уравнения (3.91) приведем его к виду 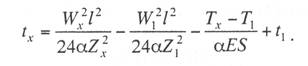 Выделив в квадратные скобки члены, имеющие постоянное значение, получим 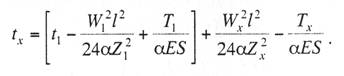 (3.92) (3.92)Величина коэффициента φ, входящего в выражения W и Z, определяется конструкцией и размещением струн вблизи опорного узла цепной подвески рассматриваемого типа цепной подвески. В применявшейся до последнего времени методике расчета цепных подвесок значение конструктивного коэффициента цепной подвески φ принималось постоянным и равным 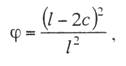 (3.93) (3.93)где с — расстояние от опор до ближайших к ним простых (нерессорных) струн. В действительности, как показал Ю. В. Флинк, значение конструктивного коэффициента φ непостоянно и изменяется в определенных пределах в зависимости от изменения натяжений несущего троса и контактного провода. При расположении простых струн на расстоянии с от опор положение контактного провода в пролете может быть представлено схемой (рис. 3.30). Рассматривая отдельно среднюю часть пролета длиной 1— 2с, ограниченную струнами СЕ и DF и учитывая, что при имеющемся расположении струн в этой части пролета φ = 1, видим, что стрелу провеса контактного провода можно определить выражением 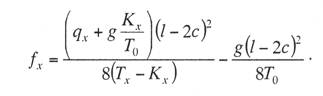 Подставляя найденное значение fx в выражение (3.83) и определяя согласно (3.85) и (3.86) значения Fx и F0 получим 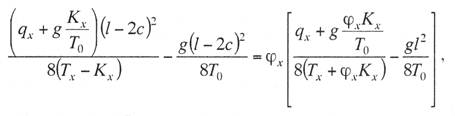 откуда после преобразований 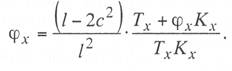 Решая это уравнение относительно φx, находим 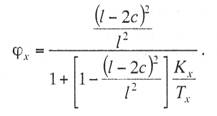 (3.94) (3.94)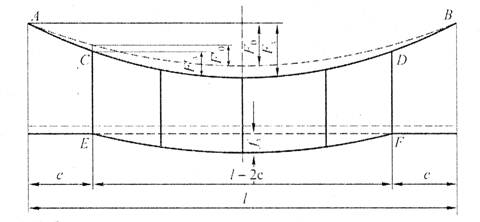 Рис. 3.30. Схема расположения проводов цепной подвески при смещенных относительно опор струнах Из выражения (3.94), полученного А. В. Фрайфельдом, видно, что величина φх зависит не только от конструктивных параметров цепной подвески, но и также от значений натяжения несущего троса и контактного провода. Сравнительные расчеты, однако, показывают, что введение переменного значения φх, значительно усложняющее расчет натяжений и стрел провеса несущего троса, не вносит существенных коррективов в их значения. Поэтому при расчетах натяжений и стрел провеса несущего троса можно без существенных погрешностей принимать φ постоянным – соответствующим среднему значению Кх/Тх . При этом для полукомпенсированной цепной подвески К = соnst и среднее значение Tx можно принимать равным Тx=0,7Tmax, для компенсированной цепной подвески К = соnst и Т = соnst, поэтому φ постоянно и зависит только от конструктивных параметров цепной подвески. При значениях φ<0,2 расчет натяжений и стрел провеса несущего троса без большой погрешности можно проводить по формулам простой подвески, рассматривая трос как гибкую нить, нагруженную весом проводов цепной подвески и дополнительными внешними нагрузками на эти провода. Для расчета полукомпенсированной цепной подвески, где К = соnst и Тх – Т1 = Zx – Z1, уравнение (3.91) может быть приведено к виду 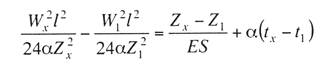 (3.95) (3.95)или 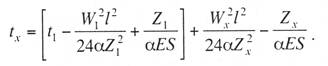 (3.96) (3.96)Для расчета некомпенсированных цепных подвесок, где Тх=Zх-φКх и Т1=Z1-φК1, уравнение (3.91) приводится к виду 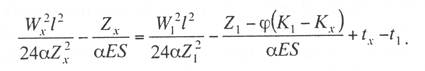 (3.97) (3.97)Для решения этого уравнения и построения кривой Тх = f(tx) необходимо предварительно определить зависимость Kх = f(tx). Натяжения контактного провода можно определить по форму лам простой подвески, полагая l равным среднему расстоянию между струнами. Так как это расстояние невелико, можно для упрощения расчета принять, что провод подвешен на бесконечно большом числе струн, пренебрегая, таким образом, влиянием стрел провеса контактного провода на величину его натяжения. Если контактный провод имеет по концам постоянное закрепление (не компенсирован), то можно считать, что длина его остается неизменной, т.е. сумма температурных и упругих удлинений контактного провода равна нулю. Отсюда легко могут быть найдены величины натяжений контактного провода К при некомпенсированной подвеске. Для этого обозначим: Ек — модуль упругости контактного провода, кг/мм2; αк — температурный коэффициент линейного расширения матери ала контактного провода; Sк – сечение контактного провода, мм2. Тогда 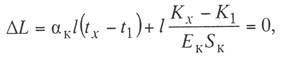 откуда Полагая что tк и tmin и K1=Kmax, получим В случае применения сезонного регулирования натяжения контактных проводов формула (3.98) дает значения натяжений лишь для зимнего периода. В летний период величина натяжения провода будет определяться по этой же формуле, но tmin – температура, при которой для летнего периода регулировки контактному проводу дается наибольшее допускаемое натяжение. При полукомпенсированной цепной подвеске К= соnst. При двойной цепной подвеске величины Кх и К1 представляю собой значения суммы натяжений вспомогательного и контактных проводов при соответствующих режимах, для определения этих значений необходимо произвести также механический расчет вспомогательного провода. При компенсированных вспомогательном и контактных проводах значение К остается постоянным Во все написанные выше виды уравнений для определения натяжений несущего троса входят приведенные нагрузки W и приведенные натяжения Z, значения которых определяются входящей в них величиной Т0 – натяжения несущего троса при режиме беспровесного положения контактных проводов, Величину Т0 можно определить из уравнения (3.91). Для этого величины с индексом «1» в уравнении (3.91) следует отнести к исходному режиму, при котором Т1 =Tmax (наибольшему допускаемому натяжению), а величины с индексом «х» – к режиму беспровесного положения контактного провода, т. е. принять tx=t0 и Тx= Т0. Величины Z и W получат при этом следующие значения: 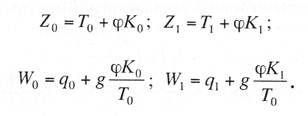 Если значение К1 определено заранее (в случае некомпенсированной цепной подвески), то после указанных подстановок в уравнении окажется только одно неизвестное — Т0. После соответствующих преобразований уравнение приводится к виду где 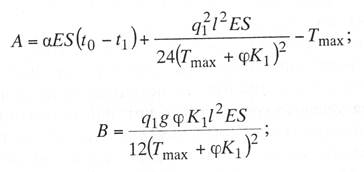 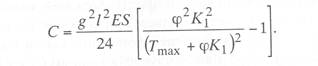 Проще определить значение Т0 непосредственно из уравнения (3.92). Для этого, заменив в уравнении величины Z и W указанными выше значениями и приняв Т1 = Тmax и Tx=T0, подставим в правой части уравнения вместо Т0 произвольную величину, близкую к ожидаемому при этом режиме значению натяжения троса, после чего определим соответствующее значение tx, которое получится в общем случае неравным принятому значению t0. Подставив затем другое значение Т0 и определив соответствующее значение tx можно вычислить действительное значение Т0 интерполяцией. Значения Т0 при подстановке нужно выбирать таким образом, чтобы tx получа лось в одном случае больше, а в другом случае меньше t0. После того как определены все величины, входящие в выражения Z и W можно определить зависимость пользуясь уравнением (3.92), после чего по формуле (3.89) могут быть найдены соответствующие значения стрел провеса несущего троса. Так как в уравнения (3.91) и (3.92) входят значения температуры t1 и результирующей нагрузки q1, при которых натяжение несущего троса Т1 = Тmах, то для решения этих уравнений и определения величины Т0 необходимо предварительно оценить, какой из расчетных режимов – режим наинизшей температуры или гололедный — надо принять за исходный. |
