Информатика и ИКТ лекция. Протокол умс от 201 г. Проректор по умр с. П. Ермишин
 Скачать 5.78 Mb. Скачать 5.78 Mb.
|
Формы представления чиселВ информатике применяется две формы представления чисел: - естественная форма с фиксированной точкой (запятой), - нормальная (экспоненциальная) форма или с плавающей точкой (запятой). В общем случае, запись любого числа в позиционной системе счисления с основанием «Р» представляет собой ряд вида: a m-1*P m-1 + a m-2*P m-2 + ….. a 1*P 1 + a 0*P 0 + a -1*P –1 + ….. a -s*P –s (1) где: m – определяет положение цифры в числе, т.е. разряд, начиная с целой части влево; s – разряд, начиная с дробной части вправо. Максимальное целое число, которое может быть представлено в “m” разрядах: N max = P m-1 Минимальное число, которое можно записать в “S “ разрядах дробной части: N min = P –s Общее количество чисел может быть: M = P m+s Двоичная система счисленияПолучила наибольшее распространение в информатике, т.к. внутреннее представление информации в ЭВМ также является двоичным. Для перевода чисел в десятичную систему используется формула (1): Пример: 1101 (2) =1*23 + 1*22+ 0*21 + 1*20 341,5 (8) = 3*82 + 4*81 + 1*80 5*8-1 A1F,4 (16) = 10*162 + 1*161 +15*160 + 4*16-1 Правила перевода чисел из десятичной системы в двоичную:
Пример: 19(10) = 10011(2)  Для перевода дробной части надо умножить ее на 2. Целая часть произведения будет первой цифрой числа в двоичной системе. Затем дробную часть у полученного результата вновь умножают на 2 и т.д. Пример: 0,73 (10) = 0,1011(2) 0,73 * 2 = 1,46 целая часть (1) 0,46 * 2 = 0,92 (0) 0,92 * 2 = 1,84 (1) 0,84 * 2 = 1,68 (1) Правила выполнения простейших арифметических действий. Сложение в двоичной системесчисления осуществляется по правилам 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 210 = 102 (единица идет в старший разряд). Таблица вычитания в двоичной системесчисления имеет вид 0 – 0 = 0, 1 – 0 = 1, 1 – 1 = 0, 0 – 1 = 10 – 1 = 1 (единицу забираем у старшего разряда). Таблица умножения в двоичной системесчисления имеет вид 0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1. Таблица деления в двоичной системесчисленияимеет вид 0 : 0 = не определено, 1 : 0 = не определено, 0 : 1 = 0, 1 : 1 = 1. Пример. Сложить двоичные числа 11012 и 110112. Запишем слагаемые в столбик и пронумеруем разряды, присвоив младшему разряду номер 1: 5 4 3 2 1 1 1 0 1 + 1 1 0 1 1 1 0 1 0 0 0 Процесс образования результата по разрядам:
Проверим результат. Для этого определим полные значения слагаемых и результата: 11012 = 1*23 +1*22 + 0*21 + 1*20 = 8 + 4 + 1 = 13; 110112 = 1*24 + 1*23 + 0*22 + 1*21 + 1*20 = 16 + 8 + 2 + 1 = 27; 1010002 = 1*25 + 0*24 + 1*23 + 0*22 + 0*21 + 0*21 = 32 + 8 = 40. Поскольку 13 + 27 = 40, двоичное сложение выполнено верно. 1.4. Основные понятия алгебры логики. Логические основы ЭВМ. При записи тех или иных логических выражений используется специальный язык, который принят в математической логике. Основоположником математической логики является великий немецкий математик Готфрид Вильгельм Лейбниц (1646 - 1716 гг.). Он сделал попытку построить универсальный язык, с помощью которого споры между людьми можно было бы разрешать посредством вычислений. На заложенном Лейбницем фундаменте ирландский математик Джордж Буль построил здание новой науки - математической логики, - которая в отличие от обычной алгебры оперирует не числами, а высказываниями. В честь Д.Буля логические переменные в языке программирования Паскаль впоследствии назвали булевскими. Высказывание - это любое утверждение, относительно которого можно сказать истинно оно или ложно, т.е. соответствует оно действительности или нет. Таким образом по своей сути высказывания фактически являются двоичными объектами и поэтому часто истинному значению высказывания ставят в соответствие 1, а ложному - 0. Например, запись А = 1 означает, что высказывание А истинно. Высказывания могут быть простыми и сложными. Простые соответствуют алгебраическим переменным, а сложные являются аналогом алгебраических функций. Функции могут получаться путем объединения переменных с помощью логических действий. Самой простой логической операцией является операция НЕ (по-другому ее часто называют отрицанием, дополнением или инверсией и обозначают NOT X или Логическая операция НЕ является унарной, т.е. имеет всего один операнд. В отличие от нее, операции И (AND) и ИЛИ (OR) являются бинарными, так как представляют собой результаты действий над двумя логическими величинами. Операцию НЕ можно задать в виде таблицы
Логическое И еще часто называют конъюнкцией, или логическим умножением. Операция И имеет результат «истина» только в том случае, если оба ее операнда истинны. Принято обозначать значком «&»либо «^» Например, рассмотрим высказывание «Для остановки ОС «Windows'95» требуется процессор не ниже 80386 и не менее 4 Мбайт оперативной памяти». Из него следует, что установка будет успешной только при одновременном выполнении обоих условий: даже если у вас в машине Pentium, но мало ОЗУ (равно как и при 8 Мбайт ОЗУ процессор 80286), «Windows'95» работать откажется.
Операция ИЛИ -дизъюнкцией, или логическим сложением . Она дает «истину», если значение «истина» имеет хотя бы один из операндов. Принято обозначать значком «
Приведенные выше таблицы значений переменных для логических операций называются таблицами истинности. В них указываются все возможные комбинации логических переменных Х и Y, а также соответствующие им результаты операций. Таблица истинности может рассматриваться в качестве одного из способов задания логической функции. Операции И, ИЛИ, НЕ образуют полную систему логических операций, из которой можно построить сколь угодно сложное логическое выражение. В вычислительной технике также часто используется операция исключающее ИЛИ (XOR), которая отличается от обыкновенного ИЛИ только при Х=1 и Y=l. Как видно из табл. 1.2, операция XOR фактически сравнивает на совпадение два двоичных разряда. Хотя теоретически основными базовыми логическими операциями всегда называют именно И, ИЛИ, НЕ, на практике по технологическим причинам в качестве основного логического элемента используется элемент И-НЕ (последняя колонка в табл. 1.2). Таблица 1.2. Дополнительные логические операции
Можно проверить, что на базе элементов И-НЕ могут быть скомпонованы все базовые логические элементы (И, ИЛИ, НЕ), а значит и любые другие, более сложные. Для упрощения логических выражений используют законы алгебры логики. Таблица 1.3. Законы алгебры логики 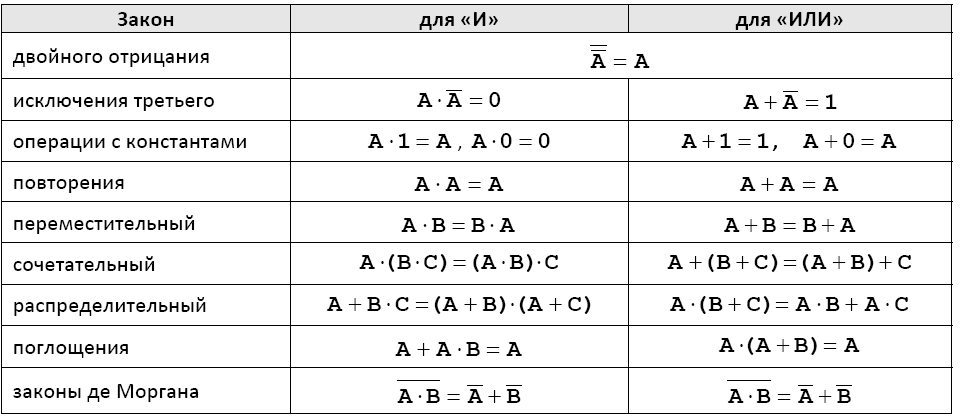 В компьютерах все вычисления выполняются с помощью логических элементов –электронных схем, выполняющих логические операции. Обозначения простейших элементов приводиться в таблице (ГОСТ 2.743-91). Обратите внимания, что небольшой кружок на выходе обозначает операцию НЕ (инверсию). 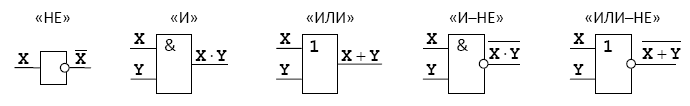 Если нужно составить схему по известному логическому выражению, ее начинают строить с конца. Находят операцию, которая будет выполняться последней, и ставят на выходе соответствующий логический элемент. Затем повторяют то же самое для сигналов, поступающих на вход этого элемента. В конце концов, должны остаться только исходные сигналы –переменные в логическом выражении. Составим схему, соответствующую выражению 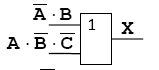 Добавляем элемент И: 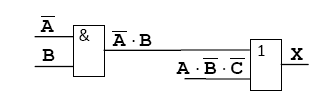 Ставим элемент НЕ: 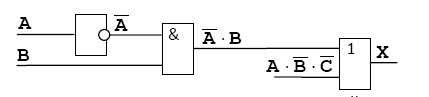 Аналогично разбираем вторую ветку: 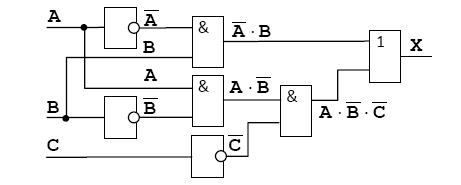 Схема составлена, ее входами являются сигналы А, В и С, а выходом Х. Тема 2. Информационные модели и системы Многие открытия в различных науках были сделаны именно благодаря построению моделей различных объектов, процессов и явлений. Например, открытие кислорода стало возможным благодаря опытам по сгоранию некоторых веществ, а сконструированные модели летательных аппаратов Циолковским привело к созданию космических кораблей и спутников, которые были выведены на орбиту Земли в середине 20 века. Модели всегда играли важную роль в деятельности человека, некоторые явления безопаснее исследовать на модели, нежели в реальности (изучение молнии, последствия атомного взрыва, ядерную энергию и т.д.) В процессе построения модели выделяются главные, наиболее существенные свойства объекта. Модель — это новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса. В разных науках одни и те же объекты исследуются под разными углами зрения и строятся различные типы моделей. Один и тот же объект иногда имеет множество моделей, а разные объекты могут описываться одной моделью. Модели классифицируются по:
Предметные модели воспроизводят геометрические, физические и другие свойства объектов в материальной форме (глобус, модель кристаллической решетки, детские игрушки и др.). Модели знаковые (информационные) представляют объекты и процессы в форме рисунков, схем, таблиц, текстов и т.д. Информационные модели в свою очередь бывают компьютерные и некомпьютерные. Модели — представления объектов или процессов реального или вымышленного мира. Укрупненная классификация абстрактных (идеальных) моделей такова. 1. Вербальные (текстовые) модели. Эти модели используют последовательности предложений на формализованных диалектах естественного языка для описания той или иной области действительности (примерами такого рода моделей являются милицейский протокол, правила дорожного движения). 2. Математические модели - очень широкий класс знаковых моделей (основанных на формальных языках над конечными алфавитами), широко использующих те или иные математические методы. Например, можно рассмотреть математическую модель звезды. Эта модель будет представлять собой сложнуюсистему уравнений, описывающих физические процессы, происходящие в недрах звезды. Математической моделью другого рода являются, например, математические соотношения, позволяющие рассчитать оптимальный (наилучший с экономической точки зрения) план работы какого-либо предприятия. 3. Информационные модели - класс знаковых моделей, описывающих информационные процессы (возникновение, передачу, преобразование и использование информации) в системах самой разнообразной природы. Граница между вербальными, математическими и информационными моделями может быть проведена весьма условно; вполне возможно считать информационные модели подклассом математических моделей. Однако, в рамках информатики как самостоятельной науки, отделенной от математики, физики, лингвистики и других наук, выделение информационных моделей в отдельный класс является целесообразным. Отметим, что существуют и иные подходы к классификации абстрактных моделей; общепринятая точка зрения здесь еще не установилась. В частности, есть тенденция резкого расширения содержания понятия «информационная модель». при котором информационное моделирование включает в себя и вербальные, и математические модели. 2.1. Информационная модель объектаОстановимся на информационных моделях, отражающих процессы возникновения, передачи, преобразования и использования информации в системах различной природы. Начнем с определения простейших понятий информационного моделирования. Экземпляром будем называть представление предмета реального мира с помощью некоторого набора его характеристик, существенных для решения данной информационной задачи (служащей контекстом построения информационной модели). Множество экземпляров, имеющих одни и те же характеристики и подчиняющиеся одним и тем же правилам, называется объектом. 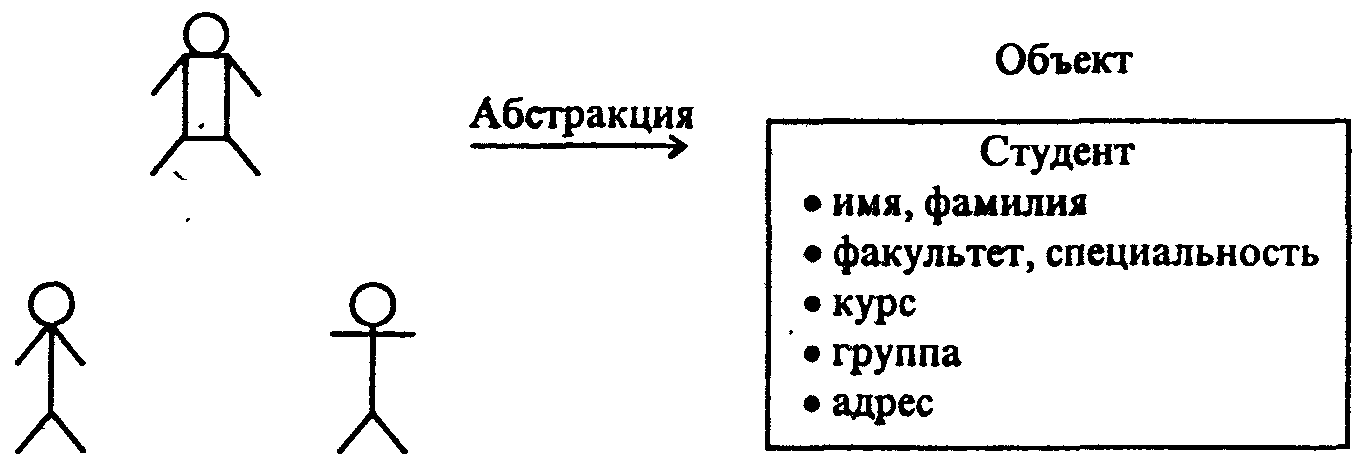 Рис. 2.1. Пример абстрагирования при построении информационной модели Таким образом, объект есть абстракция предметов реального мира, объединяемых общими характеристиками и поведением, рис. 2.1. Информационная модель какой-либо реальной системы состоит из объектов. Каждый объект в модели должен быть обеспечен уникальным и значимым именем (а также идентификатором, служащим ключом для указания этого объекта, связи его с другими объектами модели). Таким образом обозначение, наименование объекта -это элементарная процедура, лежащая в основе информационного моделирования. Объект представляет собой один типичный (но неопределенный) экземпляр чего-то в реальном мире и является простейшей информационной моделью. Объекты представляют некие «сущности» предметов реального мира, связанные с решаемой задачей. Большинство объектов, с которыми приходится встречаться, относятся к одной из следующих категорий:
Реальный объект - это абстракция физически существующих предметов. Например, на автомобильном заводе это кузов автомобиля, двигатель, коробка передач; при перевозке грузов это контейнер, средство перевозки. Роль - абстракция цели или назначения человека, части оборудования или учреждения (организации). Например, в университете как в учебном заведении это студент, преподаватель, декан; в университете как в учреждении это приемная комиссия, отдел кадров, бухгалтерия, деканат. Событие - абстракция чего-то случившегося. Например, поступление заявления от абитуриента в приемную комиссию Университета, сдача (или несдача) экзамена. Взаимодействия - объекты, получаемые из отношений между другими объектами. Например, сделка, контракт (договор) между двумя сторонами, свидетельство об образовании, выдаваемое учебным заведением его выпускнику. Объекты-спецификации используются для представления правил, стандартов или критериев качества. Например, перечень знаний, умений и навыков выпускника математического факультета, рецепт проявления фотопленки. Для каждого объекта должно существовать его описание - короткое информационное утверждение, позволяющее установить, является некоторый предмет экземпляром объекта или нет. Например, описание объекта «Абитуриент университета» может быть следующим: человек в возрасте до 35 лет, имеющий среднее образование, подавший в приемную комиссию документы и заявление о приеме. Предметы реального мира имеют характеристики (такие, например, как имя, название, регистрационный номер, дата изготовления, вес и т.д.). Каждая отдельная характеристика, общая для всех возможных экземпляров объекта, называется атрибутом. Для каждого экземпляра атрибут принимает определенное значение. Так, объект Книга имеет атрибуты Автор, Название, Год издания. Число страниц. У каждого объекта должен быть идентификатор - множество из одного или более атрибутов, значения которых определяют каждый экземпляр объекта. Для книги атрибуты Автор и Название совместно образуют идентификатор. В тоже время Год издания и Число страниц идентификаторами быть не могут - ни врозь, ни совместно, так как не определяют объект. Объект может иметь и несколько идентификаторов, каждый из которых составлен из одного или нескольких атрибутов. Один из них может быть выбран как привилегированный для соответствующей ситуации. Объект может быть представлен вместе со своими атрибутами несколькими различными способами. Графически объект может быть изображен в виде рамки, содержащей имя объекта и имена атрибутов. Атрибуты, которые составляют привилегированный идентификатор объекта, могут быть выделены (например, символом * слева от имени атрибута):  В эквивалентном текстовом представлении это может иметь следующий вид: Книга (Автор. Название. Год издания. Число страниц). Привилегированный идентификатор подчеркивается. Еще одним способом представления объекта информационной модели является таблица. В этой интерпретации каждый экземпляр объекта является строкой в таблице, а значения атрибутов, соответствующих каждому экземпляру, - клетками строки, табл. 2.1. Таблица 2.1 Таблица как представление информационной модели
Можно классифицировать атрибуты по принадлежности к одному из трех различных типов: • описательные; • указывающие; • вспомогательные. Описательные атрибуты представляют факты, внутренне присущие каждому экземпляру объекта. Если значение описательного атрибута изменится, то это говорит о том, что некоторая характеристика экземпляра изменилась, но сам экземпляр остался прежним. Указательные атрибуты могут использоваться как идентификаторы (или часть идентификаторов) экземпляра. Если значение указывающих атрибутов изменяется, то это говорит лишь о том, что новое имя дается тому же самому экземпляру. Вспомогательные атрибуты используются для связи экземпляра одного объекта с экземпляром другого объекта. Рассмотрим пример: Автомобиль * гос. номер . марка . цвет . владелец Атрибут «цвет» является описательным, атрибуты «гос. номер» и «марка» - указательными, атрибут «владелец» - вспомогательным, служащим для связи экземпляра объекта Автомобиль с экземпляром объекта Автолюбитель. Если значение вспомогательного атрибута изменится, это говорит о том, что теперь другие экземпляры объектов связаны между собой. 2.2. Алгоритм и его свойства. Структура алгоритма. Алгоритм — точное и понятное предписание исполнителю совеpшить последовательность действий, направленных на решение поставленной задачи. Алгоритм – система точно сформулированных правил, определяющая процесс преобразования допустимых исходных данных (входной информации) в желаемый результат (выходную информацию) за конечное число шагов. Название "алгоритм" произошло от латинской формы имени среднеазиатского математика аль-Хорезми — Algorithmi. Алгоритм — одно из основных понятий информатики и математики. Основные свойства алгоритмов следующие:
Формы представления алгоритмов.
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке. Например. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел. Алгоритм может быть следующим:
Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Словесный способ не имеет широкого распространения по следующим причинам: • такие описания строго не формализуемы; • страдают многословностью записей; • допускают неоднозначность толкования отдельных предписаний. Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным. Такое графическое представление называется схемой алгоритма или блок-схемой. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Описание алгоритма с помощью блок схем осуществляется рисованием последовательности геометрических фигур, каждая из которых подразумевает выполнение определенного действия алгоритма. Порядок выполнения действий указывается стрелками. Написание алгоритмов с помощью блок-схем регламентируется ГОСТом. 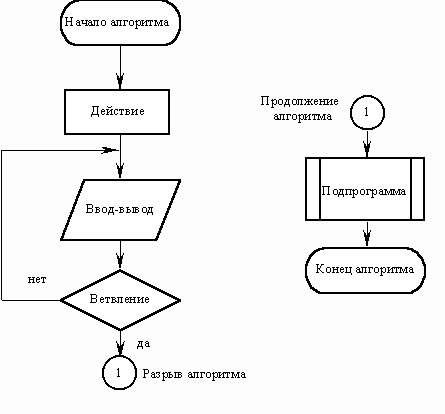 В зависимости от последовательности выполнения действий в алгоритме выделяют алгоритмы линейной, разветвленной и циклической структуры. В алгоритмах линейной структуры действия выполняются последовательно одно за другим: 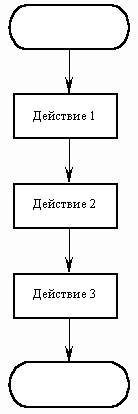 В алгоритмах разветвленной структуры в зависимости от выполнения или невыполнения какого-либо условия производятся различные последовательности действий. Каждая такая последовательность действий называется ветвью алгоритма. 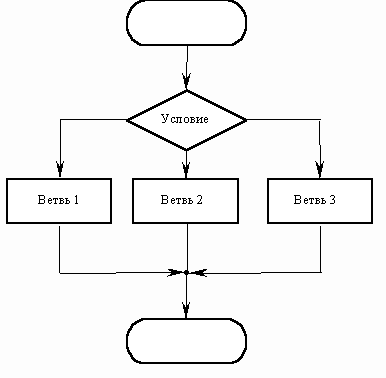 В алгоритмах циклической структуры в зависимости от выполнения или невыполнения какого-либо условия выполняется повторяющаяся последовательность действий, называющаяся телом цикла. Вложенным называется цикл, находящийся внутри тела другого цикла. Различают циклы с предусловием и послеусловием: 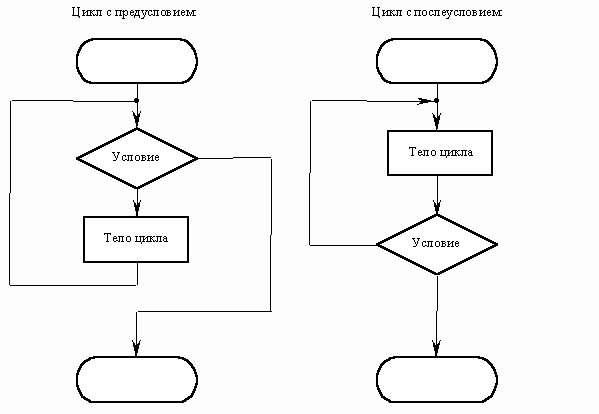 Итерационным называется цикл, число повторений которого не задается, а определяется в ходе выполнения цикла. В этом случае одно повторение цикла называется итерацией. Цикл — разновидность управляющей конструкции в высокоуровневых языках программирования, предназначенная для организации многократного исполнения набора инструкций. Также циклом может называться любая многократно исполняемая последовательность инструкций, организованная любым способом (например, с помощью условного перехода). Тема 3. Средства и технологии создания и преобразования информационных объектов 3.1. Текстовые процессоры Текстовый процессор — вид прикладной компьютерной программы, предназначенной для производства (включая набор, редактирование, форматирование, иногда печать) любого вида печатной информации. Иногда текстовый процессор называют текстовым редактором второго рода. Текстовыми процессорами в 1970-е — 1980-е годы называли предназначенные для набора и печати текстов машины индивидуального и офисного использования, состоящие из клавиатуры, встроенного компьютера для простейшего редактирования текста, а также электрического печатного устройства. Позднее наименование «текстовый процессор» стало использоваться для компьютерных программ, предназначенных для аналогичного использования. Текстовые процессоры, в отличие от текстовых редакторов, имеют больше возможностей для форматирования текста, внедрения в него графики, формул, таблиц и других объектов. Поэтому они могут быть использованы не только для набора текстов, но и для создания различного рода документов, в том числе официальных. Классическим примером текстового процессора является Microsoft Word. Программы для работы с текстами можно разделить на простые текстовые процессоры, мощные текстовые процессоры и издательские системы. Известные текстовые процессоры • AbiWord • Adobe InCopy • JWPce — текстовый процессор для японского языка. • Lotus WordPro • Microsoft Word • Microsoft Works • OpenOffice.org Writer • PolyEdit • WordPad — входит в дистрибутив MS Windows • WordPerfect 3.2. Электронные таблицы Электронные таблицы (или табличные процессоры) - это прикладные программы, предназначенные для проведения табличных расчетов. Появление электронных таблиц исторически совпадает с началом распространения персональных компьютеров. Первая программа для работы с электронными таблицами — табличный процессор, была создана в 1979 году, предназначалась для компьютеров типа Apple II и называлась VisiCalc. В 1982 году появляется знаменитый табличный процессор Lotus 1-2-3, предназначенный для IBM PC. Lotus объединял в себе вычислительные возможности электронных таблиц, деловую графику и функции реляционной СУБД. Популярность табличных процессоров росла очень быстро. Появлялись но-вые программные продукты этого класса: Multiplan, Quattro Pro, SuperCalc и другие. Одним из самых популярных табличных процессоров сегодня является MS Excel, входящий в состав пакета Microsoft Office. Что же такое электронная таблица? Это средство информационных технологий, позволяющее решать целый комплекс задач: 1. Прежде всего, выполнение вычислений. Издавна многие расчеты выполняются в табличной форме, особенно в области делопроизводства: многочисленные расчетные ведомости, табуляграммы, сметы расходов и т. п. Кроме того, решение численными методами целого ряда математических задач; удобно выполнять в табличной форме. Электронные таблицы представляют собой удобный инструмент для автоматизации таких вычислений. Решения многих вычислительных задач на ЭВМ, которые раньше можно было осуществить только путем программирования, стало возможно реализовать 2. Математическое моделирование. Использование математических формул в ЭТ позволяет представить взаимосвязь между различными параметрами некоторой реальной системы. Основное свойство ЭТ — мгновенный пересчет формул при изменении значений входящих в них операндов. Благодаря этому свойству, таблица представляет собой удобный инструмент для организации численного эксперимента: подбор параметров, прогноз поведения моделируемой системы, анализ зависимостей, планирование. Дополнительные удобства для моделирования дает возможность графического представления данных (диаграммы); 3. Использование электронной таблицы в качестве базы данных. Конечно, по сравнению с СУБД электронные таблицы имеют меньшие возможности в этой области. Однако некоторые операции манипулирования данными, свойственные реляционным СУБД, в них реализованы. Это поиск информации по заданным условиям и сортировка информации. В электронных таблицах предусмотрен также графический режим работы, который дает возможность графического представления (в виде графиков, диаграмм) числовой информации, содержащейся в таблице. Основные типы данных: • числа, как в обычном, так и экспоненциальном формате, • текст – последовательность символов, состоящая из букв, цифр и пробелов, • формулы. Формулы должны начинаться со знака равенства, и могут включать в себя числа, имена ячеек, функции (математические, статистические, финансовые, текстовые, дата и время и т.д.) и знаки математических операций. Электронные таблицы просты в обращении, быстро осваиваются непрофессиональными пользователями компьютера и во много раз упрощают и ускоряют работу бухгалтеров, экономистов, ученых. 3.3. Базы данных В настоящее время успешное функционирование различных фирм, организаций и предприятий просто не возможно без развитой информационной системы, которая позволяет автоматизировать сбор и обработку данных. Обычно для хранения и доступа к данным, содержащим сведения о некоторой предметной области, создается база данных. База данных (БД) — именованная совокупность данных, отражающая состояние объектов и их отношений в рассматриваемой предметной области. Под предметной областью принято понимать некоторую область человеческой деятельности или область реального мира, подлежащих изучению для организации управления и автоматизации, например, предприятие, вуз и.т.д. Система управления базами данных (СУБД) — совокупность языковых и программных средств, предназначенных для создания, наполнения, обновления и удаления баз данных. Система специальным образом организованных данных – баз данных, программных, технических, языковых, организационно-методических средств, предназначенных для обеспечения централизованного накопления и коллективного многоцелевого использования называется банком данных Программы, с помощью которых пользователи работают с базой данных, называются приложениями. В общем случае с одной базой данных могут работать множество различных приложений. Например, если база данных моделирует некоторое предприятие, то для работы с ней может быть создано приложение, которое обслуживает подсистему учета кадров, другое приложение может быть посвящено работе подсистемы расчета заработной платы сотрудников, третье приложение работает как подсистемы складского учета, четвертое приложение посвящено планированию производственного процесса. При рассмотрении приложений, работающих с одной базой данных, предполагается, что они могут работать параллельно и независимо друг от друга, и именно СУБД призвана обеспечить работу множества приложений с единой базой данных таким образом, чтобы каждое из них выполнялось корректно, то учитывало все изменения в базе данных, вносимые другими приложениями. Для поиска информации в базах данных используется информационно-поисковая система. Информационно-поисковая система опирается на базу данных, в которой осуществляется поиск нужных документов по заявкам пользователей. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
