Практическая работа. Практическая работа 6. Проверка на адекватность действительности построенной модели надежности технической системы на базе корреляционного анализа
 Скачать 139.37 Kb. Скачать 139.37 Kb.
|
|
Практическая работа № 6 ПРОВЕРКА НА АДЕКВАТНОСТЬ ДЕЙСТВИТЕЛЬНОСТИ ПОСТРОЕННОЙ МОДЕЛИ НАДЕЖНОСТИ ТЕХНИЧЕСКОЙ СИСТЕМЫ НА БАЗЕ КОРРЕЛЯЦИОННОГО АНАЛИЗА В исследованиях надежности технических и технологических систем одной из важных задач является анализ стохастической (вероятностной) зависимости между изучаемыми переменными. Для оценки тесноты и направления связи между изучаемыми переменными используются показатели корреляции. Линейный коэффициент корреляции характеризует (измеряет) степень тесноты линейной зависимости между двумя коррелируемыми признаками. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать или убывать по линейному закону. Если две исследуемые случайные величины X и Y связаны точной линейной функциональной зависимостью, то коэффициент корреляции равен ±1, т. е. RXY = ±1. Знак «минус» означает, что при возрастании одной случайной величины другая имеет тенденцию убывать. В общем случае, когда случайные величины X и Y связаны произвольной вероятностной зависимостью, линейный коэффициент корреляции R принимает значение в пределах от 1 до − 1 (–1 < RXY < 1). Тогда качественная оценка тесноты связи случайных величин может быть определена по шкале Чеддока, приводимой в таблице 1 в зависимости от коэффициента корреляции. Таким образом, по значению коэффициента корреляции можно определить тесноту и направление связи между статистическими и теоретическими моделями надежности объектов систем газонефтепроводов, построенных на основании разных гипотез и разными методами Excel, т. е. проверить соответствие построенных теоретических моделей статистическим моделям. Таблица 1  Комплекс методов статистической обработки данных, представленный в виде пунктов меню «Анализ данных» в Excel, позволяет проводить анализ статистических данных. Каждый метод реализован в виде отдельного режима работы. Доступ к методу «Корреляция» осуществляется с помощью цепочки команд «Сервис – Анализ данных – Корреляция» (см. рис. 1).  Рисунок 1. Пункты меню «Анализ данных» в Excel Постановка задачи Используя метод «Корреляция» (см. рис. 1), проверить степень достоверности теоретических моделей, полученных в работе №5 (первая – получена с помощью линии тренда, вторая с помощью метода наименьших квадратов), определяющей распределение времени безотказной работы технической системы. Определить: Наиболее точную теоретическую модель надежности технической системы среди полученных разными способами в практической работе № 5, для чего определить: Коэффициент корреляции между эмпирической  и теоретическими и теоретическими  и и  ) моделями распределения времени безотказной работы; ) моделями распределения времени безотказной работы; Степень тесноты связи между эмпирической  и теоретическими и теоретическими  и и  ) моделями распределения времени безотказной работы по рассчитанным коэффициентам корреляции на основе шкалы Чеддока, приводимой в табл. 1.; ) моделями распределения времени безотказной работы по рассчитанным коэффициентам корреляции на основе шкалы Чеддока, приводимой в табл. 1.;•Сделать вывод о достоверности теоретических моделей безотказной работы технической системы. Решение (на примере варианта из практической работы №4). На основании данных практической работы 5 и приведенных в таблице 2 вычислим средние значения  , ,  и и  : :X=  Y=  Y=     Где n – количество интервалов. Вычислим средние квадратичные отклонения по формулам 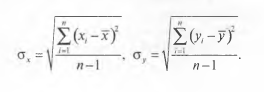  0.2540746 0.2540746 0.246567 0.246567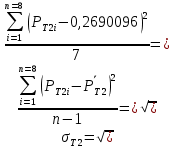 0.2583197. 0.2583197.Значения коэффициентов корреляции между эмпирическими и теоретическими данными определяются как: 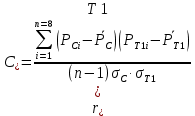 = = =0.99369 =0.99369 =0.99521 =0.99521В соответствии со Шкалой Чеддока можно сделать вывод, что связь является весьма высокой, т. е. в результате компьютерного моделирования мы получили модель надежности, адекватную действительности. Выводы: Рассчитаны значения коэффициентов корреляции между эмпирическими и теоретическими данными. Коэффициент корреляции между эмпирическими данными и теоретическими, полученными с помощью уравнения линии тренда составил 0.99369. Коэффициент корреляции между эмпирическими данными и теоретическими, полученными с помощью метода среднего квадратичного отклонения составил 0.99521. В соответствии со Шкалой Чеддока можно сделать вывод, что связь в обоих случаях является весьма высокой, т. е. в результате компьютерного моделирования мы получили модель надежности, адекватную действительности. Таблица 2 Результаты расчета (данные из практической работы №4)
|



