методы модел. Пусть количество выпускаемой первой продукции x, а количество второй y, тогда выручка от продажи всей продукции

• Название: Пусть количество выпускаемой первой продукции x, а количество второй y, тогда выручка от продажи всей продукции
• Дата: 25.04.2023
• Размер: 118.66 Kb.
• Имя файла: методы модел.docx
• Тип: Задача; #1088276
• страница: 1 из 7

Задача 1

Пусть количество выпускаемой первой продукции – x, а количество второй – y, тогда выручка от продажи всей продукции:

F(x) = 12000x + 13000y → max

при условиях:

y ≤ 3

10x ≤ 50

8x + 14y ≤ 56

7x + 8y ≤ 56

Неравенства заменяем на равенства. Строим линии ограничений:

y = 3

x = 5

y = 4 – 4/7x

y = 7 – 7/8x

Область допустимых значений – выпуклый многоугольник OACD.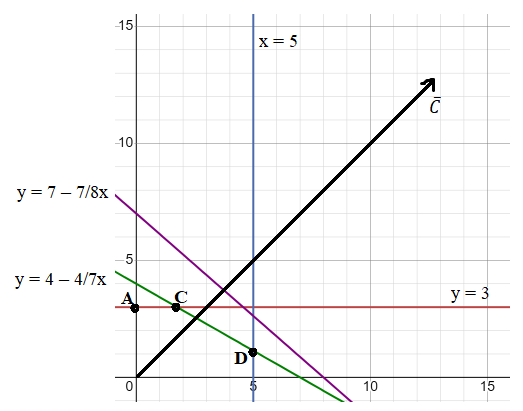



Строится направляющий вектор C.

Строится перпендикуляр к вектору С через начало координат.

Точка С является точкой оптимума. Находим координаты точки оптимума. Приравниваем уравнения 1 и 3.

3 = 4 – 4/7x

x = 1,75

y = 3

Координаты точки С (1,75; 3).

Находим значение целевой функции точки оптимума.

F(C) = 12000 * 1,75 + 13000 * 3 = 60 000

Для определения прибыли необходимо вычесть затраты:

П_х = 21 000 – 120 * 10 * 1,75 – 50 * 8 * 1,75 – 200 * 7 *1,75 – 4000 = 11 750

П_y = 39 000 – 6000 * 1 * 3 – 50 * 14 * 3 – 200 * 8 * 3 – 2700 = 14 100

Прибыль = 11 750 + 14 100 = 25 850

Ответ: необходимо выпускать 1,75 единицы первого вида продукции, 3 единицы второго вида продукции, при этом прибыль будет максимальной, и будет равна 25 850 денежных единиц.

Задача 2

Провести анализ результатов стоимости перевозок однородного груза при решении транспортной задачи согласно методам:

• 
  Северо-западного угла;
  
• 
  Двойного предпочтения;
  
• 
  Аппроксимации Ролля.
  

В качестве исходных данных задачи выступают:

Матрица расстояний:



Потребности пунктов назначения:

b₁ = 200, b₂ = 40, b₃ = 50, b₄ = 110, b₅ = 50

Запасы на пунктах отправления:

A₁ = 200, a₂ = 150, a₃ = 100

Метод северо-западного угла

Запасы поставщиков: 200 + 150 + 100 = 450 единиц продукции.

Потребность потребителей: 200 + 40 + 50 + 110 + 50 = 450 единиц продукции.

Суммарные запасы продукции у поставщиков равны суммарной потребности потребителей.

Начинаем заполнять таблицу от левого верхнего угла и постепенно "двигаемся" к правому нижнему.
От северо-запада к юго-востоку.

Поставщик	Потребитель						Запас
	B 1	B 2	B 3	B 4	B 5
A 1	? 32	20	34	40	24	200
A 2	28	18	24	34	21	150
A 3	26	16	22	32	30	100
Потребность	200	40	50	110	50

Поставщик	Потребитель					Запас
	B 1	B 2	B 3	B 4	B 5
A 1	200 32	20	34	40	24		200   нет
A 2	? 28	18	24	34	21		150
A 3	26	16	22	32	30		100
Потребность	200 0	40	50	110	50

Поставщик	Потребитель						Запас
	B 1	B 2	B 3	B 4	B 5
A 1	200 32	0 20	0 34	0 40	0 24	200   нет
A 2	0 28	? 18	24	34	21	150   150
A 3	0 26	16	22	32	30	100
Потребность	200 нет	40	50	110	50

Поставщик	Потребитель					Запас
	B 1	B 2	B 3	B 4	B 5
A 1	200 32	0 20	0 34	0 40	0 24	200   нет
A 2	0 28	40 18	? 24	34	21	150   150   110
A 3	0 26	0 16	22	32	30	100
Потребность	200 нет	40 нет	50	110	50