Дифференциальные операторы в криволинейных системах координат. диф операторы в криволинейной СК. Пусть в некоторой области
 Скачать 63.61 Kb.
|
|
Пусть в некоторой области D с криволинейной системой координат  задано скалярное поле Если векторы  образуют базис в некоторой точке M, то градиент скалярного поля u в этой точке определяется формулой где  – коэффициенты Ламе. В частности, 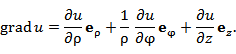 в цилиндрической системе координат   В сферических координатах 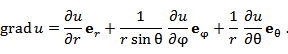   Пусть в области D задано векторное поле  Здесь  - криволинейные координаты точки  ; - единичные касательные векторы координатных -линий соответственно. Дивергенция векторного поля 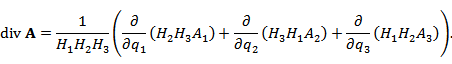A в точке M с криволинейными координатами определяется формулой В цилиндрической системе координат 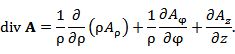  В сферической системе координат 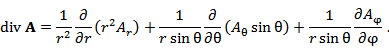  Ротор векторного поля A в точке M с криволинейными координатами 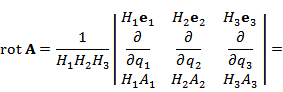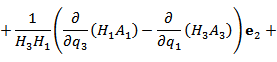определяется формулой    В цилиндрической системе координат 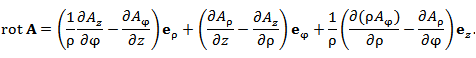 В сферических координатах 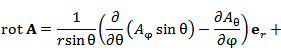 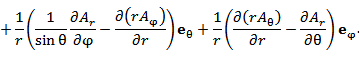 Операторы grad, div и rot представляют собой линейные дифференциальные операции. Оператор grad определен на дифференцируемых скалярных полях и сопоставляет им векторные поля, тогда как операторы div и rot определены на дифференцируемых векторных полях. Оператор div ставит им в соответствие скалярные поля, а оператор rot – векторные поля. Действие оператора Лапласа на скалярную функцию u определяется формулой 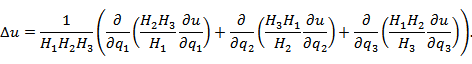 В цилиндрической системе координат  В сферической системе координат  |