Основными параметрами движения потоков жидкости в открытых канал. Q и массовом расходе
 Скачать 39.55 Kb.
|
|
Основными параметрами движения потоков жидкости в открытых каналах или внутри трубопроводов, а также потоков пара, газа или плазмы являются расход, т. е. количество вещества, протекающее через какое-либо сечение потока в единицу времени, и общее количество протекшего вещества. Расход и количество связаны между собой точно так же, как скорость и путь при движении твердых тел. И ту и другую величину можно выразить через единицы объема и массы, соответственно говоря об объемном расходе Q и массовом расходе М. Иногда интересуются также скоростью v потока, которая может быть местной (в данной точке сечения потока), усредненной по некоторой части сечения потока и средней по всему сечению. Измерение количества жидкости, газа и пара производится либо путем периодического отмеривания одинаковых объемных или массовых доз вещества, либо путем интегрирования расхода. Первый метод, как правило, осуществляется с помощью чисто механических средств, и поэтому ниже рассматриваются только методы, связанные с измерением расхода. Особенностью приборов для измерения расходов является малое значение их динамического диапазона, редко превышающее Dп = 10 ÷15, в то время как величина измеряемых расходов может лежать в диапазоне от 10-3 до нескольких тысяч кубометров в час. Расходомеры с преобразованием в перепад давления состоят чаще всего из некоторого сужающего устройства (диафрагма, сопло и т. д.) и дифференциального манометра, измеряющего перепад давления, создаваемый сужающим устройством. Объемный и массовый расходы выражаются соответственно формулами: Q = v·S, M = ρ·Q, Где v – средняя по сечению скорость потока, ρ· плотность жидкости, S — площадь поперечного сечения канала. Трубка Вентури представляет собой трубу сечения S1, плавно сужающуюся к сечению S2. Принцип действия трубки Вентури основан на измерении разности давлений потока жидкости в узком и широком сечениях трубы. Согласно уравнению Бернулли, там, где скорость непрерывного и стационарного потока сплошной среды выше (например, v1), давление в потоке p1 ниже, и наоборот:  Используя соотношение неразрывности v1·S1 = v2·S2, получаем среднюю скорость потока в трубе в узком сечении S2. 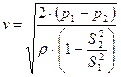 В таком случае объёмный расход равен  μ - коэффициент расхода, который учитывает неидеальность жидкости (наличие внутреннего трения в жидкости).  На рисунке показано сужение трубы и присоединение к трубке Вентури дифференциального манометра.Поскольку перепад давления пропорционален квадрату расхода, дифференциальные манометры снабжаются различными устройствами для извлечения квадратного корня (например, датчик уравновешивания с ферродинамическим обратным преобразователем, развивающий уравновешивающую силу, пропорциональную квадрату тока). Упрощенная схема устройства такого расходомера показана на рис. 5.1. 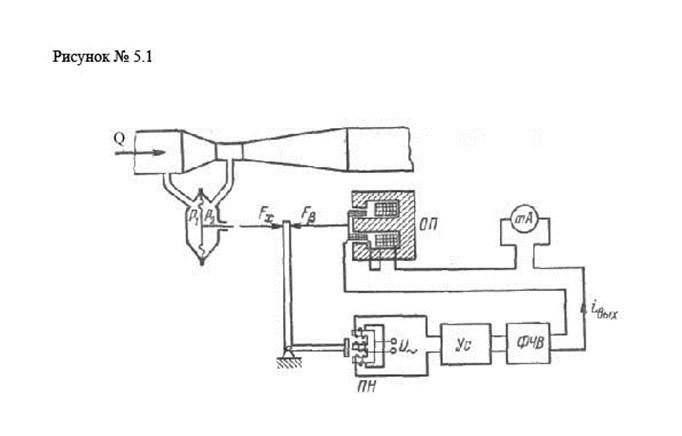 Приборы этой группы в настоящее время широко распространены. Их динамический диапазон невелик и составляет D = 3 ÷ 5. Они могут применяться для измерения расходов, как жидкостей, так и газов при температурах до сотен градусов и давлениях до десятков мегапаскалей. Погрешность их составляет 1—2%. |