программа Занимательная математика. Занимательная математика. 6 класс Мостовая ЕО. Рабочая программа курса внеурочной деятельности Занимательная математика

• Название: Рабочая программа курса внеурочной деятельности Занимательная математика
• Анкор: программа Занимательная математика
• Дата: 03.04.2023
• Размер: 60.52 Kb.
• Имя файла: Занимательная математика. 6 класс Мостовая ЕО.docx
• Тип: Рабочая программа; #1034345
• страница: 3 из 4

СОДЕРЖАНИЕ ПРОГРАММЫ

В большинстве случаев содержание занятий непосредственно следует из указанной темы конкретного занятия. Отбор тех или иных задач для рассмотрения на занятии определяется исключительно педагогом, ведущим внеурочную деятельность в соответствии с уровнем базовой математической подготовки учащихся, а также уровнем их мотивации и потенциальной одаренности. Весьма обширный список предлагаемой литературы без труда позволит педагогу наполнить занятие содержательными задачами сообразно своему вкусу и интересам учащихся.

Вместе с тем руководитель, реализующий программу внеурочной деятельности, должен придерживаться следующих основных правил:

• 
  Неправильно заниматься одной темой в течение продолжительного промежутка времени, даже в рамках одного занятия полезно иногда сменить направление деятельности, при этом необходимо постоянно возвращаться к пройденному. Это целесообразно делать, предлагая задачи по данной теме в устных и письменных олимпиадах и других соревнованиях.
  
• 
  В каждой теме необходимо выделить несколько основных логических
  

«вех» и добиваться безусловного понимания (а не зазубривания!) этих моментов учащимися.

• 
  Необходимо постоянно обращаться к нестандартным и «спортивным»
  

формам проведения занятий, не забывая при этом подробно разбирать все предлагаемые на них задания; необходимо использовать на занятиях развлекательные и шуточные задачи.

Подчеркивая, что подготовка и проведение занятий – это творческий процесс, в который вовлекается педагог, тем не менее, обратим внимание на ряд наиболее важных тем.
Нулевойцикл«Знакомство».

Очень многое в организации и успешности проведения внеурочной деятельности зависит от первого занятия. Возможна такая его структура:

• 
  Руководитель освещает перспективы: что будет рассматриваться на занятиях, чем учащиеся будут заниматься, каково содержание и формы работы, как организуется самостоятельная работа и домашняя работа, подготовка докладов, рефератов, мини-проектов. Важно озвучить учащимся основные требования к участникам внеурочной деятельности.
  
• 
  Учащимся предлагается несколько простых задач. Для их решения не требуется ничего, кроме здравого смысла и владения простейшими вычислительными навыками; их назначение – выявление логических и математических способностей учащихся (а в дальнейшем – в качестве эмоциональных разрядок).
  
• 
  Возможно, некоторое время следует посвятить рассказу о математике, о ее значении в жизни человека, о ее связях с другими науками.
  

Четностьинечетность.

Понятие четности. Применение идеи четности: известные утверждения. Четность суммы и разности нескольких чисел. Идея «разбиения на пары».

Задачи, в которых используется понятие четности встречаются очень часто. Поэтому желательно познакомить школьников с подходами к решению этих задач. Задачи естественным образом разбиваются на три цикла:

1. 
   Разбиение на пары.
   

Если предметы разбиты на пары, то их четное число. Следовательно, если из нечетного числа предметов образовано несколько пар, то, по крайней мере, один предмет остался без пары. Для решения таких задач нужно в каждом случае увидеть, что именно и на какие пары разбивается.

2. 
   Чередование.
   

Если из предметов двух сортов образована цепочка, в которой соседние предметы разных сортов, то на всех четных местах стоят предметы одного сорта, а на всех нечетных – другого. Отсюда вывод: предметов одного сорта на один больше, чем предметов другого сорта в случае, когда длина цепочки нечетна и предметов обоих сортов поровну, тогда длина цепочки четна.

3. 
   Чет – нечет.
   

Решение задач основано на простом наблюдении: сумма четного числа нечетных чисел – четна. Обобщение этого факта: четность суммы нескольких чисел зависит лишь от четности числа нечетных слагаемых: если количество нечетных слагаемых (не)четно, то и сумма – (не)четна.

Примеры задач:

• 
  За круглым столом сидят мальчики и девочки. Докажите, что количество пар соседей разного пола чѐтно.
  
• 
  На плоскости расположено 11 шестерѐнок, соединенных в кольцо. Могут ли
  

все шестерѐнки вращаться одновременно?

• 
  Шахматный конь вышел с поля a1 и через несколько ходов вернулся на него. Докажите, что он сделал чѐтное число ходов.
  
• 
  Может ли прямая не содержащая вершин замкнутой 11-звенной ломаной, пересекать все ее звенья?
  
• 
  На клетчатой бумаге нарисован замкнутый путь, идущий по линиям сетки. Может ли он иметь длину 1999? А длину 2000?
  
• 
  Улитка ползет по плоскости с постоянной скоростью, поворачивая на 90 каждые 15 минут. Докажите, что она может вернуться в исходную точку только через целое число часов.
  
• 
  Из набора домино выбросили все кости с «пустышками». Можно ли оставшиеся кости выложить в ряд по правилам?
  
• 
  Пусть расположение шашек в предыдущей задаче симметрично относительно обеих диагоналей. Докажите, что одна из шашек стоит в центральной клетке.
  

Логическиезадачи.

Среди задач на сообразительность особый интерес представляют логические задачи. Если для решения задачи требуется лишь логически мыслить и совсем не нужно производить арифметические выкладки, то такую задачу обычно называют логической. При решении подобных задач решающую роль играет правильное построение цепочки точных, иногда очень точных рассуждений.

На первом этапе целесообразно рассмотреть три широко распространенных типа логических задач:

1. 
   Задачи, в которых на основании серии посылок, сообщающих те или иные сведения о действующих лицах, требуется сделать определенные выводы.
   
2. 
   Задачи о «мудрецах».
   
3. 
   Задачи о лжецах и тех, кто всегда говорит правду.
   

Софизмы.

Софизмы – это умышленные ложные умозаключения, которые имеют вид правильных. Они обязательно содержат одну или несколько замаскированных логических ошибок. Например, в математических софизмах часто выполняются

«запрещенные» действия, такие как деление на ноль, не учитываются условия применимости формул и правил.

Софистика – направление философии, которое возникло в V-IV вв. до н.э. в Греции и стало очень популярным в Афинах. Софистами называли платных «учителей мудрости», которые учили граждан риторике, искусству слова, приемам ведения спора, красноречию. Одним из представителей софистов был философ Протагор, который говорил: «Я обучаю людей риторике, а это и есть гражданское искусство».

Софисты считали, что истина субъективна, то есть у каждого человека своя истина, человек сам создает себе истину и сам же её оценивает, поэтому в суждениях об истине очень много личного. Справедливость, как и истина, у каждого человека тоже своя, а значит, о каждой вещи можно судить двояко, то есть о каждой вещи есть два противоположных мнения. Софисты учили людей оценивать одно и то же событие, как положительное и как отрицательное одновременно, таким образом они приучали людей к широте взглядов. Первую систематизацию софизмов дал еще Аристотель в IV веке до нашей эры. Он разделил все ошибки на 2 класса «ошибки речи» и ошибки

«вне речи», то есть в мышлении.

Учащимся предлагаются для решения не только широко известные софизмы, но ставится задача сконструировать (придумать) свои софизмы.
Арифметикаостатков.

Тема является чрезвычайно важной, хотя и может показаться несколько скучной. Для первого этапа работы вполне достаточно тех теоретических сведений, которые имеют учащиеся 6 класса. В процессе работы теоретическая база может быть несколько пополнена, однако увлекаться теорией не следует. При решении задач выделяются те свойства целых чисел, которые помогают добраться до ответа. Методика работы:

Первый этап: учащиеся должны понять, что свойства делимости полностью определяются разложением числа на простые множители. Этому могут помочь следующие ключевые вопросы:

• 
  делится ли 3⁵ *2 на 3;
  
• 
  делится ли 3⁵ *2 на 4;
  
• 
  делится ли 3⁵ *2 на 5;
  
• 
  делится ли 3⁵ *2 на 6?
  
• 
  верно ли, что если натуральное число делится на 4 и на 6, то оно делится на 24?
  
• 
  число 5А делится на 3. Верно ли, что А делится на 3?
  
• 
  число А – четно. Верно ли, что 3А делится на 6?
  
• 
  число А не делится на 3. Может ли на 3 делится число 2А? и т.п.
  

Далее актуализируются определения взаимно простых чисел, наибольшего общего делителя и наименьшего общего кратного, определение деления одного целого числа на натуральное число с остатком.
Поискпредмета.

За внешне несерьезными формулировками задач скрываются идеи, которые лежат в основе больших и бурно развивающихся разделов современной математики – теории информации, теории планирования эксперимента, теории игр. Даже такое задание как отгадывание номера телефона – на самом деле представляет собой поиск способа кодирования информации, требующего наименьшего времени для передачи по каналу связи с сигналами двух типов, соответствующих ответам «да» и «нет».

Учащиеся знакомятся с недесятичными позиционными системами счисления, прежде всего, с двоичной.

На занятии в роли отгадчика может выступать учитель или один из участников, подготовивших доклад по теме (например, двоичной системе счисления), которая является ключом к решению данной задачи.
Игры

На занятиях внеурочной деятельности рассматриваются так называемые «конечные игры с полной информацией», теория которых проста и доступна школьникам. На занимательном материале учащиеся знакомятся с такими важными понятиями теории игр, как «стратегия» и «выигрышная стратегия», а также на простом и наглядном примере «изоморфизма игр» - с важнейшим для все математики понятием изоморфизм.

Поиск выигрышной стратегии требует настойчивости и упорства в достижении поставленной цели, развивает логические, комбинаторные и вычислительные способности учащихся.

Первый класс игр – игры-шутки. Это игры, исход которых не зависит от того, как играют соперники. Игры-шутки позволяют снять напряжение и усталость, дают школьникам возможность переключиться от напряженной творческой работы. Целесообразно предлагать их по одной после разбора трудного материала. Полезно перед решением, дать школьникам возможность поиграть друг с другом.

Задачи – игры весьма содержательны. При изложение их решения, необходимо, во- первых, грамотно сформулировать стратегию, а во-вторых, доказать, что она, действительно, ведет к выигрышу. Поэтому, задачи-игры чрезвычайно полезны для развития речевой математической культуры и четкого понимания того, что значит решить задачу.
ПринципДирихле.

При решении многих задач используются сходные между собой приемы рассуждений. Очевидно, что если в каждую клетку разрешается посадить не более одного зайца, то разместить 6 зайцев в 5-ти клетках не удастся и вообще, ни для какого натурального n не удастся разместить n+1 зайцев в n клетках. Можно сказать иначе: если в n клетках находится n+1 зайцев, то найдется клетка, в которой сидит не менее двух зайцев.

Сформулированное выше утверждение о зайцах-клетках имеет следующий математический смысл: при отображении множества А, содержащего n+1 элементов в множество В, содержащее n элементов, найдутся два элемента множества А, имеющие один и тот же образ. Это утверждение называется принципом Дирихле. Принцип Дирихле, несмотря на всю простоту и очевидность очень часто используется при доказательстве теорем и решении задач.

При разборе задач полезно четко разделять доказательство на поиск «зайцев» и

«клеток», на дополнительные соображения и, наконец, на применение принципа Дирихле.
Графы.

Теория графов находит свое применение в различных областях современной математики и ее многочисленных приложений, особенно экономике. Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность. Многие доказательства также упрощаются, приобретают убедительность, если воспользоваться графами, особенно это относится к комбинаторике.

Понятие графа должно появиться на занятии после того, как разобрано несколько задач, решающее соображение в которых – графическое изображение условия.

Первая и главная цель, которую нужно преследовать, занимаясь графами, - научить школьников видеть граф в условии задачи и грамотно переводить это условие на язык теории графов. Кроме того, важно, чтобы учащиеся правильно применяли теорему о четности числа нечетных вершин графа, понимали, что такое компонента связности и умели пользоваться критерием Эйлеровости.
Геометрия:задачинаразрезание.

Задачами на разрезание увлекались многие ученые с древнейших времен. Решения многих задач на разрезание были найдены еще с древними греками и китайцами. Первый систематический трактат на эту тему принадлежит перу Абул-Вефа – персидского астролога X века. Геометры всерьез занялись решением задач на разрезание фигур на наименьшее число частей и последующее составление из них той или иной новой фигуры лишь в XX веке, прежде всего, потому, что универсального

метода решения таких задач не существует и каждый, кто берется за их решение, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению. Учитывая, что здесь не требуется глубокое знание геометрии, любители могут иногда даже превзойти профессионалов-математиков.

Задачи на разрезание помогают как можно раньше формировать геометрические представления у школьников на разнообразном материале. При решении таких задач возникает ощущение красоты, закона и порядка в природе.

На первом этапе рекомендуется рассмотреть задачи на клетчатой бумаге. Задачи, в которых разрезание фигур (в основном это квадраты и прямоугольники) идет по сторонам клеток.

Далее могут рассматриваться задачи, связанные с фигурами-пентамино. Пентамино, изначально, (от др.-греч. πέντα пять, и домино) — пятиклеточные полимино, то есть плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов, соединѐнных между собой сторонами («ходом ладьи»). Сегодня пентамино понимается более широко – плоская фигура, составленная из плиток.

Задачи разбиения плоскости, в которых нужно находить сплошные разбиения прямоугольников на плитки прямоугольной формы, задачи на составление паркетов, задачи о наиболее плотной укладке фигур в прямоугольнике или квадрате, задачи, в которых одна фигура разрезается на части, из которых составляется другая фигура.

В наши дни любители головоломок увлекаются решением задач на разрезание, п Примеры задач:

• 
  Разрежьте фигуру, изображенную на рисунке, на две равные части по линиям сетки так, чтобы в каждой из частей был кружок.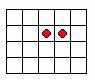
  

• 
  На клетчатой бумаге нарисован квадрат размером 5*5 клеток. Придумайте, как разрезать его по линиям сетки на 7 различных прямоугольников.
  

Комбинаторика.

В последние годы необычайно возросла роль комбинаторных методов не только в самой математике, но и в ее многочисленных приложениях: физике, химии, биологии, лингвистике, технике, экономике. Поэтому важно как можно раньше начать знакомить учащихся с комбинаторными методами и комбинаторными подходами. Изучение этой темы способствует развитию у учащихся «комбинаторного» мышления.

Главная цель, которую должен преследовать педагог при разборе и решении этих задач – осознанное понимание школьниками в какой ситуации при подсчете вариантов следует перемножать, а в какой – складывать. Для этого следует демонстрировать учащимся комбинаторные методы на большом количестве простых и конкретных примеров, продвигаясь вперед осторожно и постепенно. Не следует переходить к введению понятий «размещение» и «перестановки» пока это правило не освоено всеми учащимися.
Примерыиконструкции.

Примеры задач:

• 
  Среди четырѐх людей нет трѐх с одинаковым именем, или с одинаковым отчеством, или с одинаковой фамилией, но у каждых двух совпадает или имя, или
  

отчество, или фамилия. Может ли такое быть?

• 
  Закрасьте некоторые клетки квадрата 4х4 так, чтобы любая закрашенная клетка имела общую сторону ровно с тремя незакрашенными.
  
• 
  Как расположить 16 шашек в 10 рядов по 4 шашки в каждом ряду? Как расположить 9 шашек в 10 рядов так, чтобы в каждом ряду было по 3 шашки? (ряд – это несколько шашек, лежащих на одной линии).
  
• 
  При делении числа 2•3=6 на 4 получаем в остатке 2. При делении числа 3•4=12 на 5 получаем в остатке 2. Верно ли, что остаток от деления произведения двух последовательных чисел на число, следующее за ними, всегда равен 2?
  

Повторение.Математическоесоревнование.

По окончании цикла занятий проводится обобщающее занятие, в рамках которого проходит повторение изученного материала, а также проводится один из видов математического соревнования, который наиболее подходит для организации работы со школьниками, занятыми во внеурочной деятельности. Это может быть математический КВН, математический аукцион, математическая регата, игра по станциям, математический хоккей, математическое лото, мозговая атака и другие формы работы.
Итоговаяолимпиадапроводится как форма итогового занятия по освоению программы, определяющего объективный уровень знаний и умений учащихся, полученных в результате участия во внеурочной деятельности по математике. Мероприятие проводится по правилам проведения классической олимпиады по математике. Вариант работы составляется учителем. В работу включаются задания, которые были предметом обсуждения на занятиях внеурочной деятельности.