Рабочая программа по учебнику А. Г. Мордковича и др. Алгебра и начала анализа

• Название: Рабочая программа по учебнику А. Г. Мордковича и др. Алгебра и начала анализа
• Дата: 11.04.2022
• Размер: 0.78 Mb.
• Имя файла: rabochaya_programma_10_klass_profil_a.g.mordkovich.doc
• Тип: Рабочая программа; #463147
• страница: 7 из 7

ПРИЛОЖЕНИЕ №8.
К урокам №77,78

1). Вычислить:



2). Решить уравнение


К уроку №79

1). Отметьте на координатной плоскости точки, соответствующие комплексным числам z₁=-5-4ί, z₂=1+8ί.

2). Изобразите на координатной плоскости множество всех комплексных чисел Ζ, удовлетворяющих заданному условию:

а). действительная часть равна -2

б). мнимая часть равна 3 или 4

в). Re z = Im z

г). Re z = (Im z)²

3). Решите уравнение

а).

б).
К уроку №80

1). Найти модуль комплексного числа

6 - 8ί, ί(2+ί)

2). Изобразите на комплексной плоскости множество всех чисел Ζ, удовлетворяющих заданному условию

а). │z│=3 б). │z+2ί│=2

3). Число Ζ задано в тригонометрической форме. Укажите его стандартную тригонометрическую форму



4). Запишите комплексное число в стандартной тригонометрической форме


К уроку №81

1). Решить уравнение



2). Вычислить



3). Изобразить на комплексной плоскости число Ζ и множество

если

К урокам №82,83

1). Вычислить







,
ПРИЛОЖЕНИЕ №9.
К урокам №86,87

1. 
   Числовая последовательность (y_n ) задана формулой
   

а). Вычислите первые четыре члена данной последовательности.

б). Является ли членом последовательности число ?

2. 
   Составьте формулу n-ого члена последовательности
   

2, 5, 10, 17, 26, ….

3. 
   Постройте график последовательности
   

y_n= - (n-2)² + 4
К уроку №88

1. 
   Составьте уравнение горизонтальной асимптоты графика последовательности
   

2. 
   Вычислите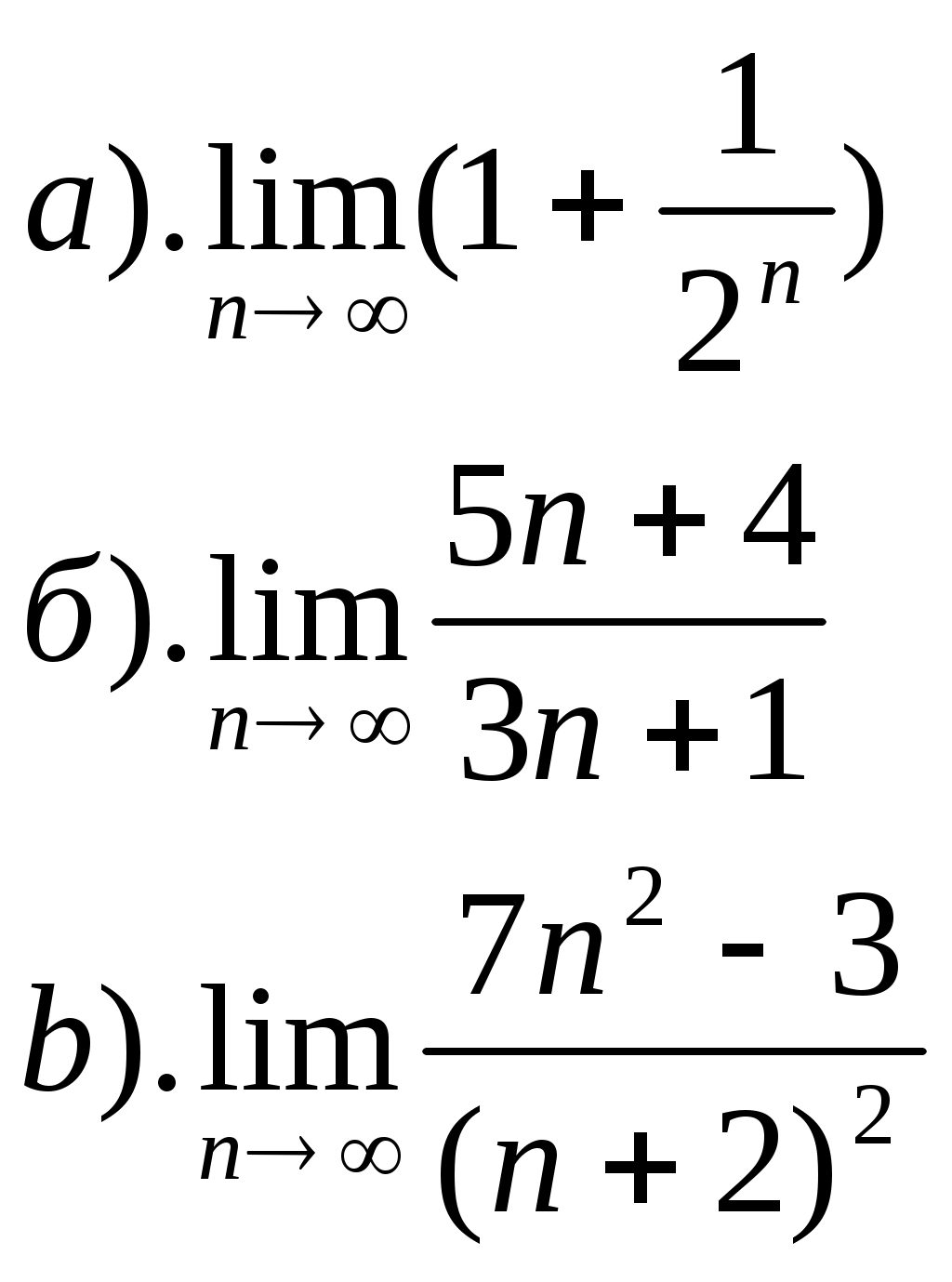
   

К уроку №89

1. 
   Найдите сумму геометрической прогрессии 9, 3, 1, ….
   
2. 
   Сумма геометрической прогрессии ( b_n ) равна 123, первый член прогрессии равен 41. Найдите знаменатель прогрессии.
   
3. 
   Найти сумму геометрической прогрессии ( b_n ), если b_n =
   

К уроку №90

Вычислите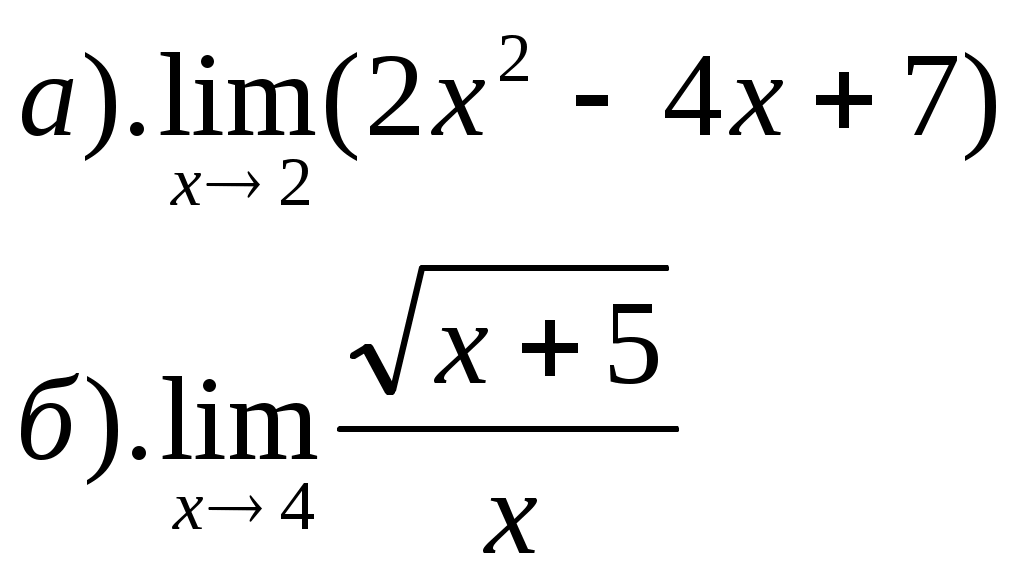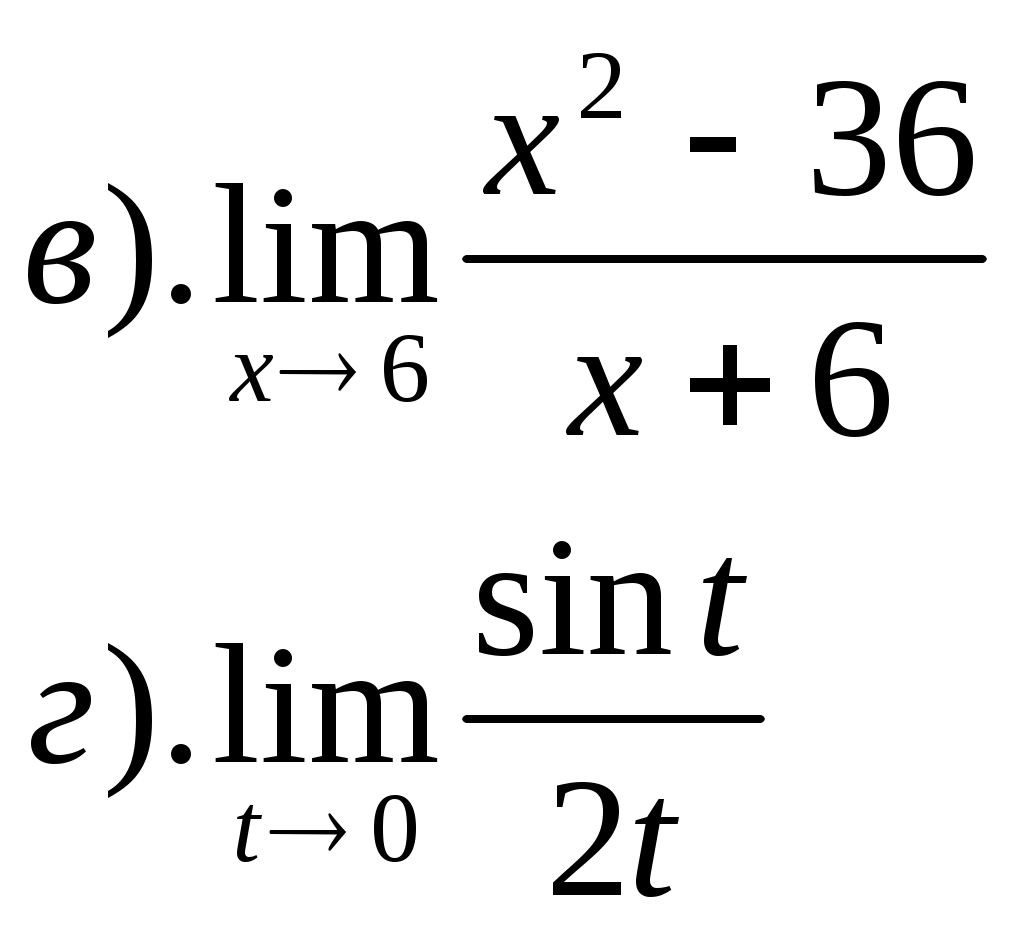



К уроку №91
Для функции y=5x+1 найдите:

а). приращение функции ∆y при переходе от точки х_о к точке х_о+∆х;

б). отношение приращения функции ∆y к приращению аргумента ∆х;

в). предел отношения приращения функции к приращению аргумента.
К уроку №92

1. 
   Закон движения точки по прямой задается формулой S(t)=t²+3, где t - время (в секундах), S(t) – отклонение точки в момент времени t (в метрах) от начального положения. Найдите мгновенную скорость движения точки в момент времени t, если t=0,75с.
   

2. 
   Определить значение f′(х) для функции y=f(x) по графику.
   

К урокам №93-96

1. 
   Найти значение производной функции y=f(x) в точке х_о, если f(x)= , х_о=25
   

2. 
   Найти скорость изменения функции y=-5х+4
   

3. 
   Найти угловой коэффициент касательной к графику функции y=f(x) в точке с абсциссой х_о, если f(x)=соsx, х_о=
   
4. 
   Найти производную функции: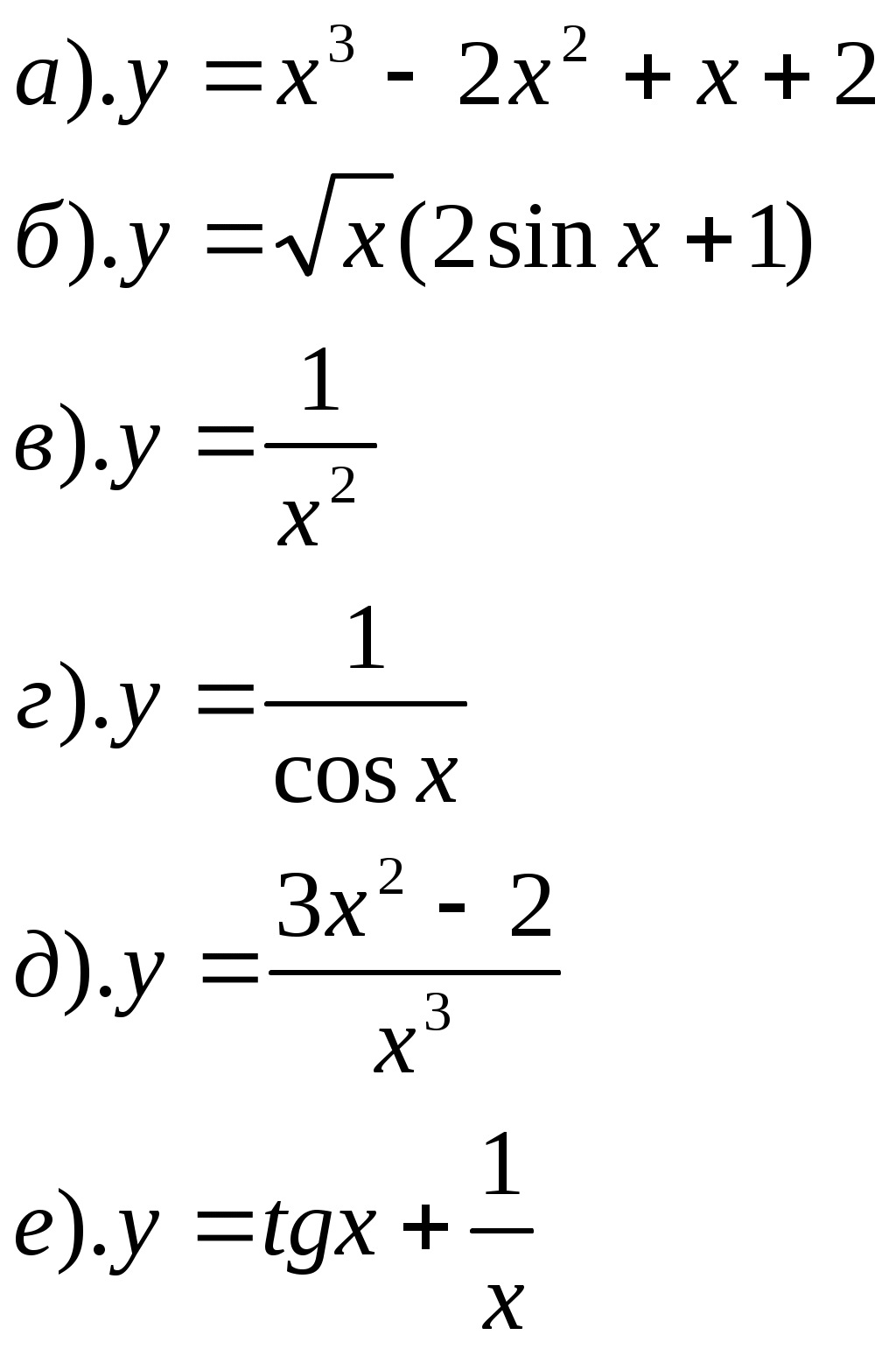
   

5. 
   Найдите тангенс угла φ между касательной к графику функции y=0,25tgx в точке с абсциссой х_о= и положительным направлением оси О_х. Определите, острым или тупым является угол φ.
   

К урокам №97-98

Найти производную функции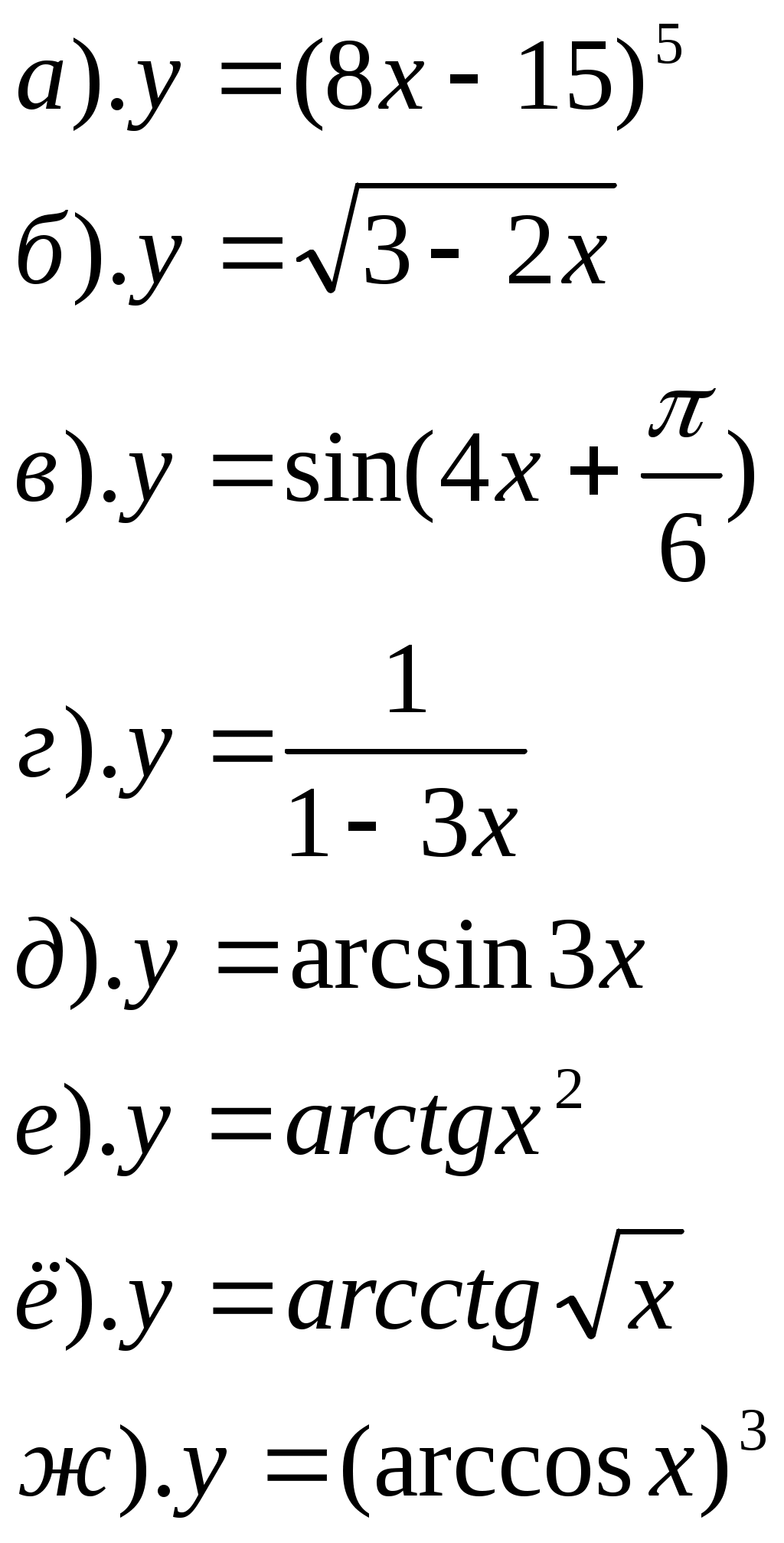


К урокам №99-100

1. 
   Найти угловой коэффициент касательной, проведенной к графику функции y=f(x) в точке с абсциссой х=а, если f(x)= , а=1
   
2. 
   Найти абсциссы точек графика функции , в которых угловой коэффициент касательной равен -1
   
3. 
   Составьте уравнение касательной к графику функции y=x³-2x²+3x+4 в точке с абсциссой х=2
   

К урокам №103-108

1. 
   Найти точки экстремума функции и определить их характер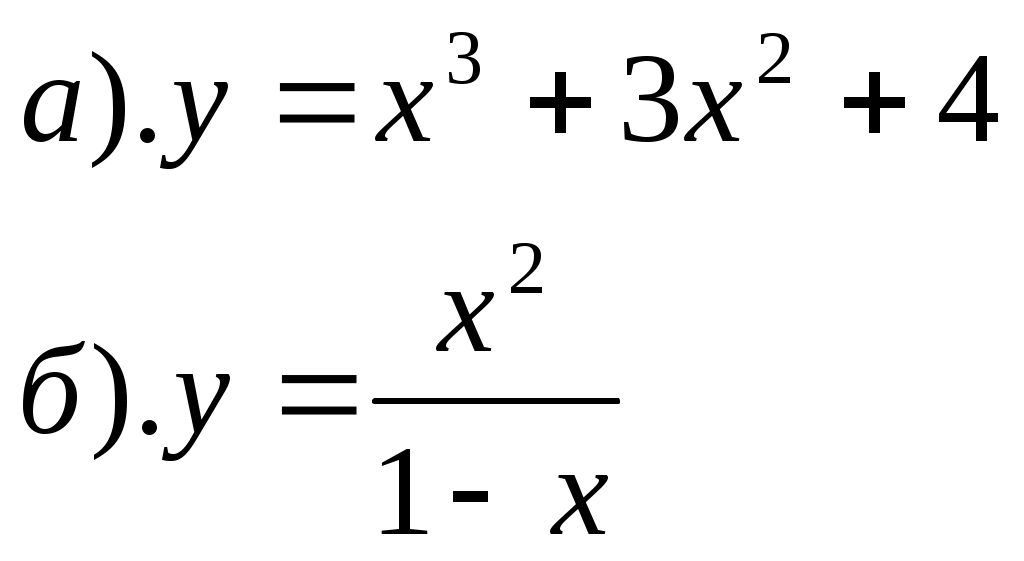
   

2. 
   Исследуйте и постройте график функции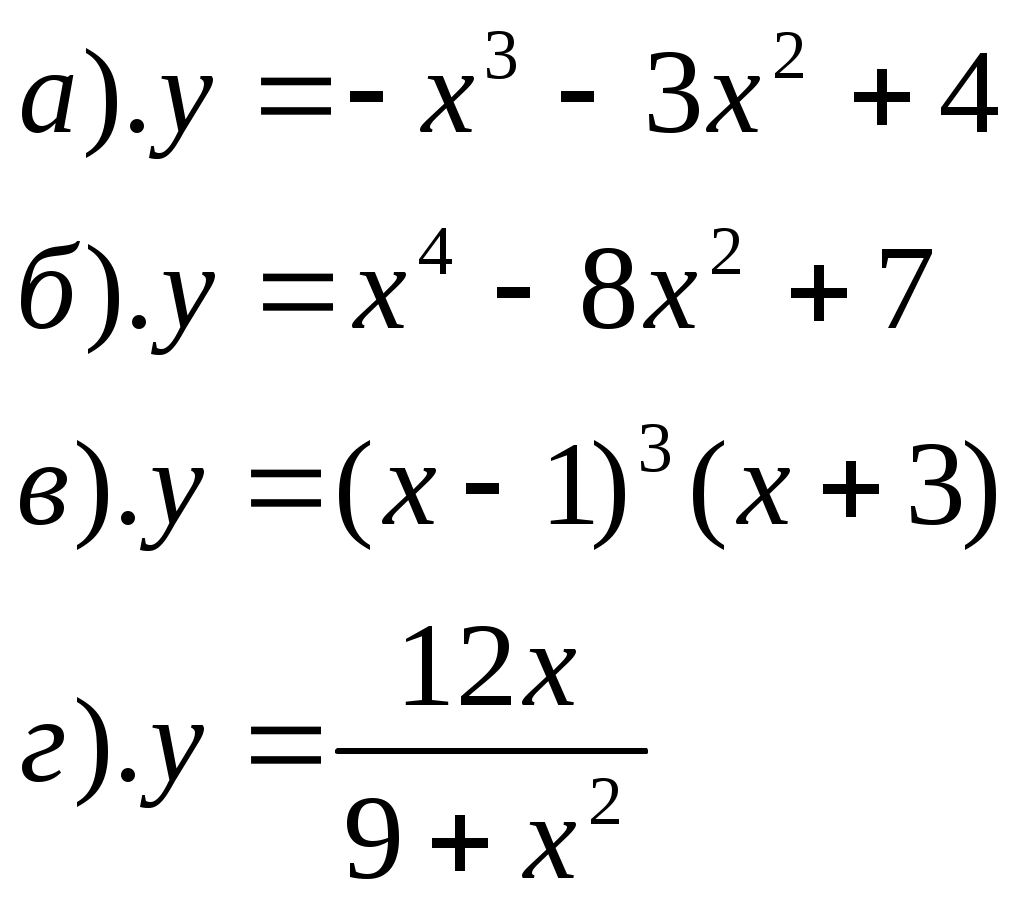
   

К урокам №109-111

1. 
   Найти наибольшее и наименьшее значение функции:
   

на отрезке [1;9]

на отрезке

2. 
   Число 16 представлено в виде произведения двух положительных множителей так, что сумма их квадратов имеет наименьшее значение. Найти эти множители.
   

ПРИЛОЖЕНИЕ №10.
К урокам №114,115

1. 
   Двузначное число составляют из цифр 0, 1, 3, 4, 5, 6, 9 (повторения цифр допустимы).
   

а). Сколько всего можно составить чисел?

б). Сколько всего можно составить чисел больших 50?

в). Сколько всего можно составить нечетных чисел?

г). Сколько всего можно составить нечетных чисел, меньших 55?

2. 
   Вычислите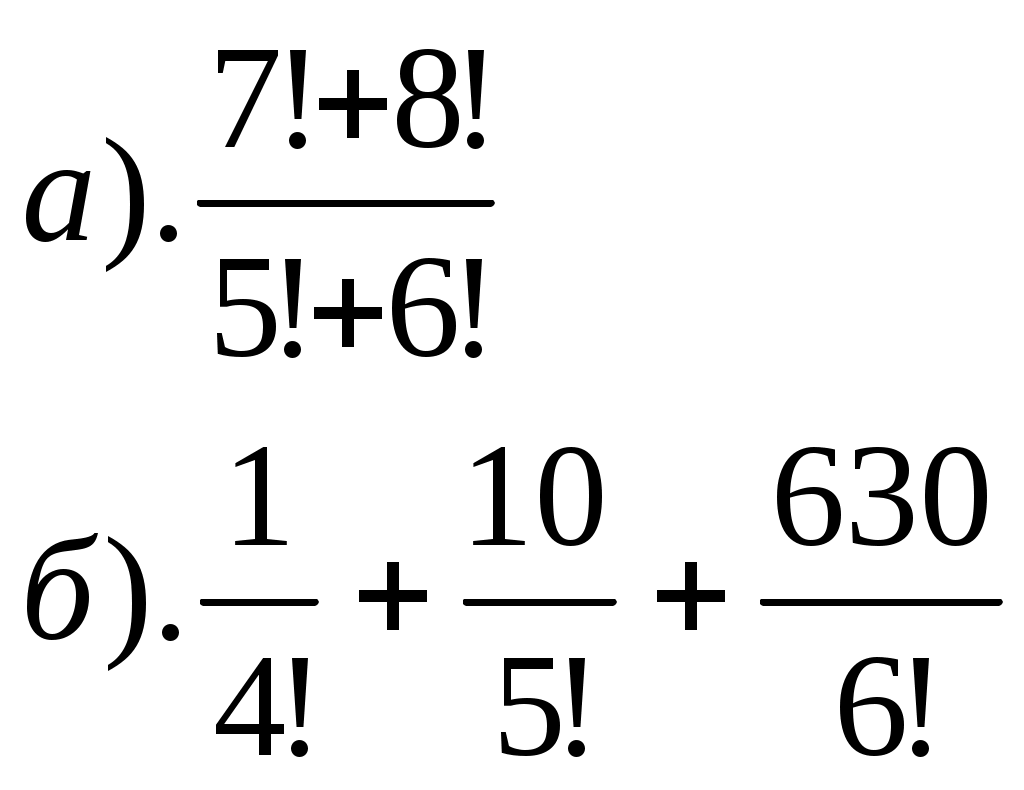
   

3. 
   Сколькими нулями оканчивается число 10!, 15!
   

К уроку №116

1. Встретились несколько человек и стали здороваться друг с другом. Рукопожатий было от 60 до 70. Сколько человек встретилось, если известно, что:

а). каждый здоровался с каждым;

б). только один человек не здоровался ни с кем;

в). только двое не поздоровались между собой;

г). четверо поздоровались только между собой и остальные поздоровались только между собой.

2. Вычислите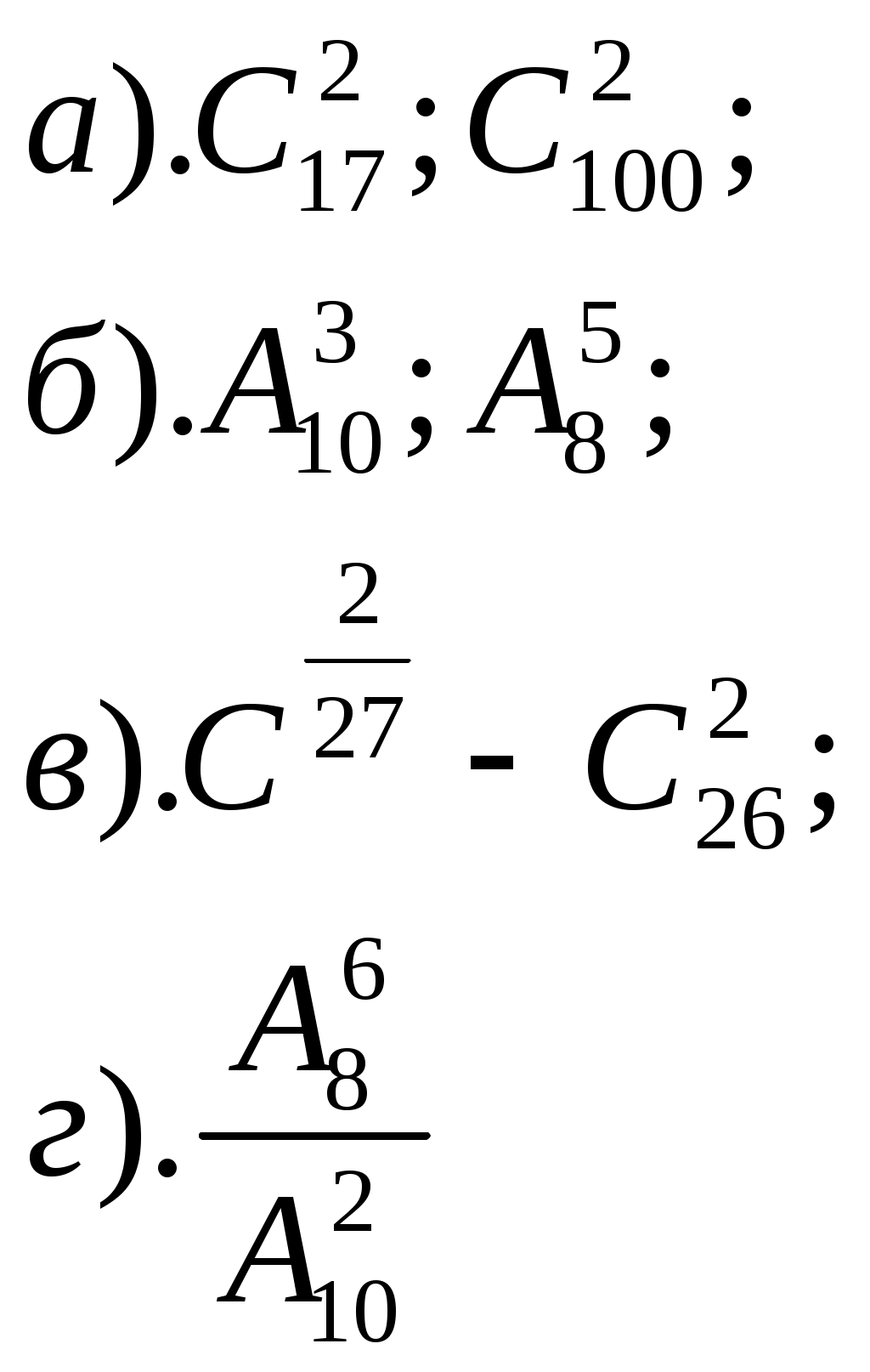



3.Решите уравнение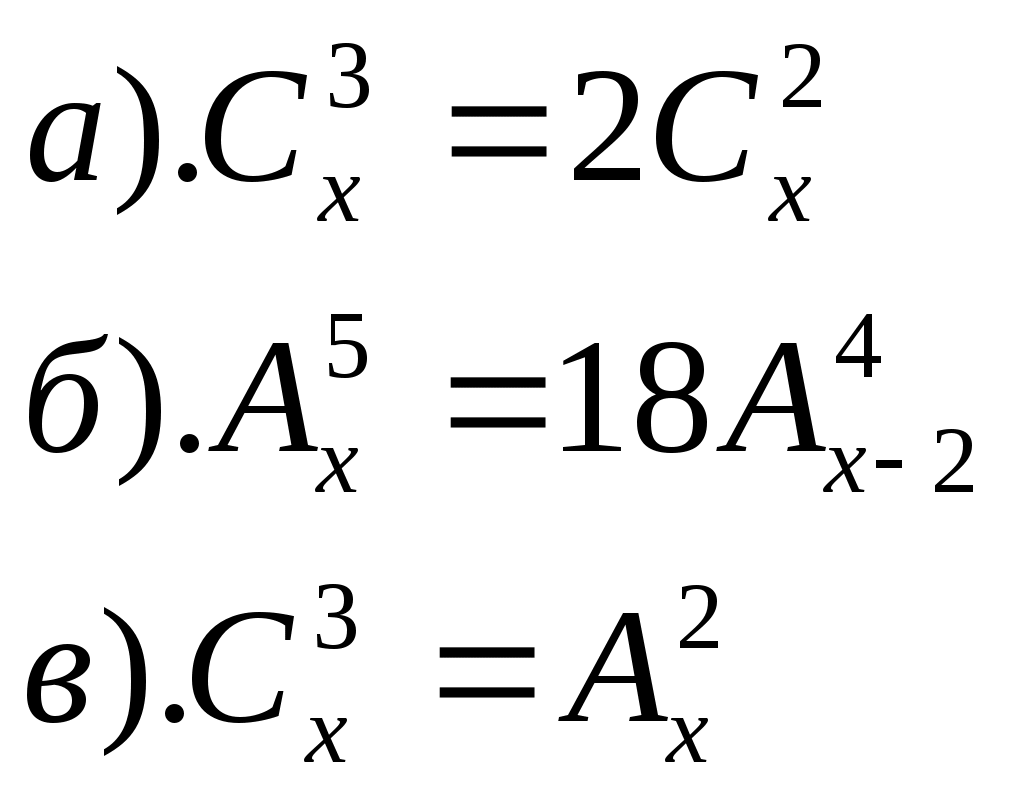


К уроку №117

Выпишите треугольник Паскаля до седьмой строки включительно.

Найдите сумму всех чисел в третьей строке треугольника Паскаля.
К урокам №118-120

1. 
   Случайным образом выбирают двузначное натуральное число. Найдите вероятность того, что оно:
   

а). делится на 5,

б). не делится на 29.

2. 
   В темном ящике 8 белых и 7 черных шаров. Вы случайно вытаскиваете одновременно 4 шара. Найдите вероятность того, что
   

а). все шары белые;

б). имеется, как минимум, три белых шара;

в). имеется, как минимум, два черных шара;

г). есть хотя бы один белый шар.