|
|
Рабочая тетрадь для самостоятельной работы
Красноярский медико-фармацевтический колледж
РАБОЧАЯ ТЕТРАДЬ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Вариант 7
Фамилия_______________________________________________
Имя___________________________________________________
Отчество_______________________________________________
Специальность __________________________________________
Группа _________ Курс_______
Период, за который представлены документы и материалы
с_______________________ 20_____ года
по______________________20______ года.
Личная подпись обучающегося ____________________
Красноярск
2010
Зачем тебе изучать математику?
 
Математическое образование является средством активного интеллектуального развития человека, его мыслительных способностей.
Человек, изучающий математические термины, утверждения, доказательства, умеющий решать задачи, вырабатывать стиль мышления, характеризующийся краткостью, лаконичностью, логикой суждений. Человек, знающий математику, и в своей профессиональной деятельности стремится строго следовать тому предписанию и набору правил, которые приводят к получению правильного результата. Поэтому одной из задач математики является высокоинтеллектуальное развитие человека, способного творчески решать поставленные задачи и адаптироваться к динамически развивающемуся обществу. С этой точки зрения, конкретные математические знания рассматриваются как основы для дальнейшей профессиональной деятельности, а сам процесс изучения математики – как развивающая функция, способствующая повышению интеллектуального уровня обучающегося.
Самоотчёт об успеваемости по математике
№
|
Наименование
|
Дата сдачи
|
оценка
|
Роспись преподавателя
|
Решение заданий:
|
|
Пределы, их свойства
|
|
|
|
|
Производная функции. Дифференциал и его приложение к приближенным вычислениям
|
|
|
|
|
Неопределенный и определенный интегралы и их свойства.
Применение определенного интеграла к решению прикладных задач
|
|
|
|
|
Дифференциальные уравнения и их применение в медицинской практике
|
|
|
|
|
Основные понятия дискретной математики.
Закон больших чисел. Теория вероятности
|
|
|
|
| Математическая статистика и ее роль в медицине и здравоохранении. Медико-демографические показатели |
|
|
|
|
Применение математических методов в профессиональной деятельности среднего медицинского персонала
|
|
|
|
|
Проведение исследования по теме «Математическая статистика и ее роль в медицине издравоохранении. Медико-демографические показатели»
|
|
|
|
Творческая работа:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Творческие работы
Написание реферата (в соответствии с требованиями к оформлению и содержанию)
Темы рефератов:
Применение математических методов в профессиональной деятельности среднего медицинского персонала.
Дифференциально-интегральные исчисления в медицинской практике.
Роль математики в медицине
Математико-статистическая обработка данных медицинских исследований
Математическая биофизика клетки
2. Создание презентации по теме самостоятельной работы
Тема: «Пределы, их свойства»
Знания:
определение функции;
определение чётности, нечётности;
определение периодической функции;
определение возрастающей, убывающей функции;
определение предела функции;
свойства пределов функций.
Умения:
производить элементарные операции с функциями;
находить область значений, область определений функций;
строить графики функций;
находить пределы функций.
Функция. Исследование функции.
Найдите область определения функции 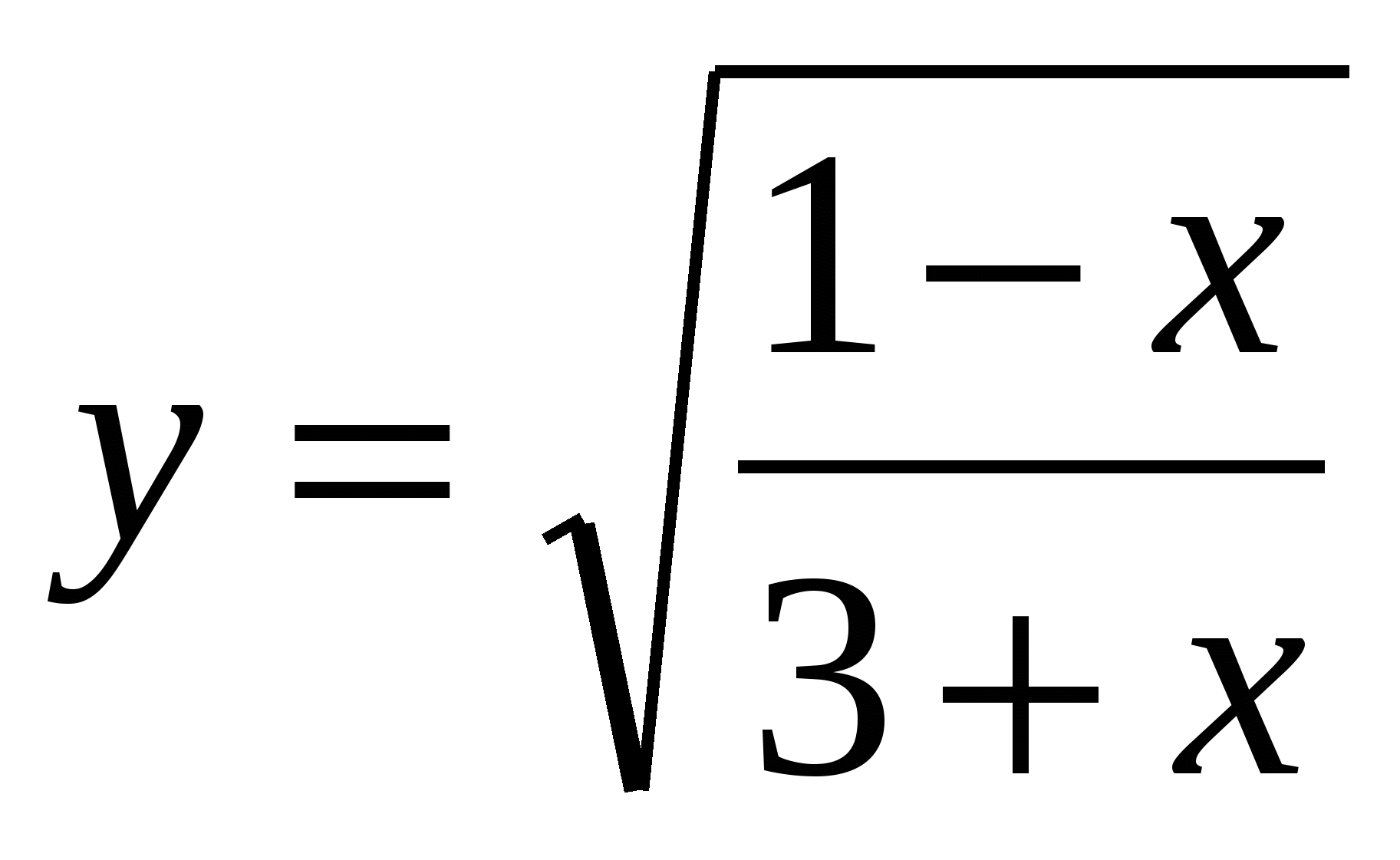
Решение:__Тема:_«Неопределенный_и_определенный_интегралы_и_их_свойства.'>Решение:__Найдите_предел_функции__Решение'>Решение:
Исследовать функцию 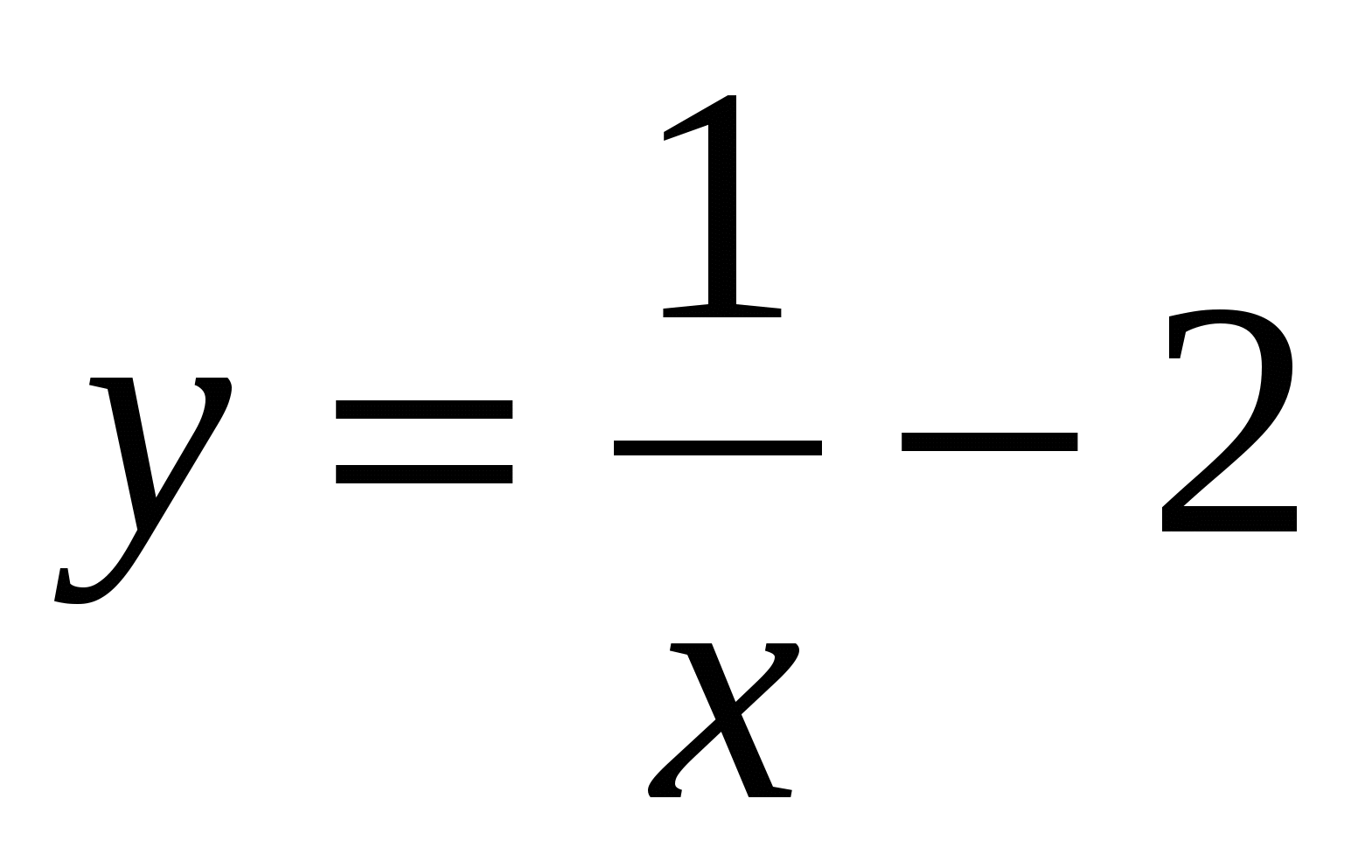 на: на:
четность;
периодичность;
непрерывность;
построить эскиз графика
Решение:
Предел функции
Найдите предел функции в точке 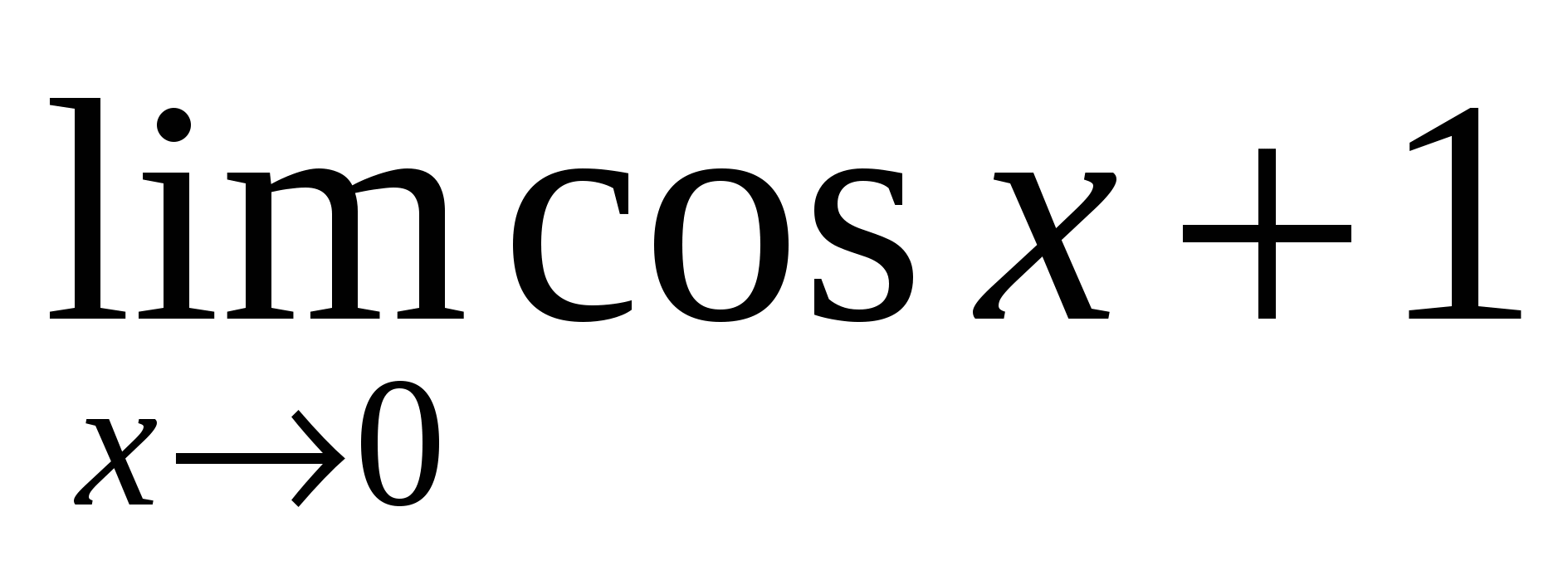
Решение:
Найдите предел функции 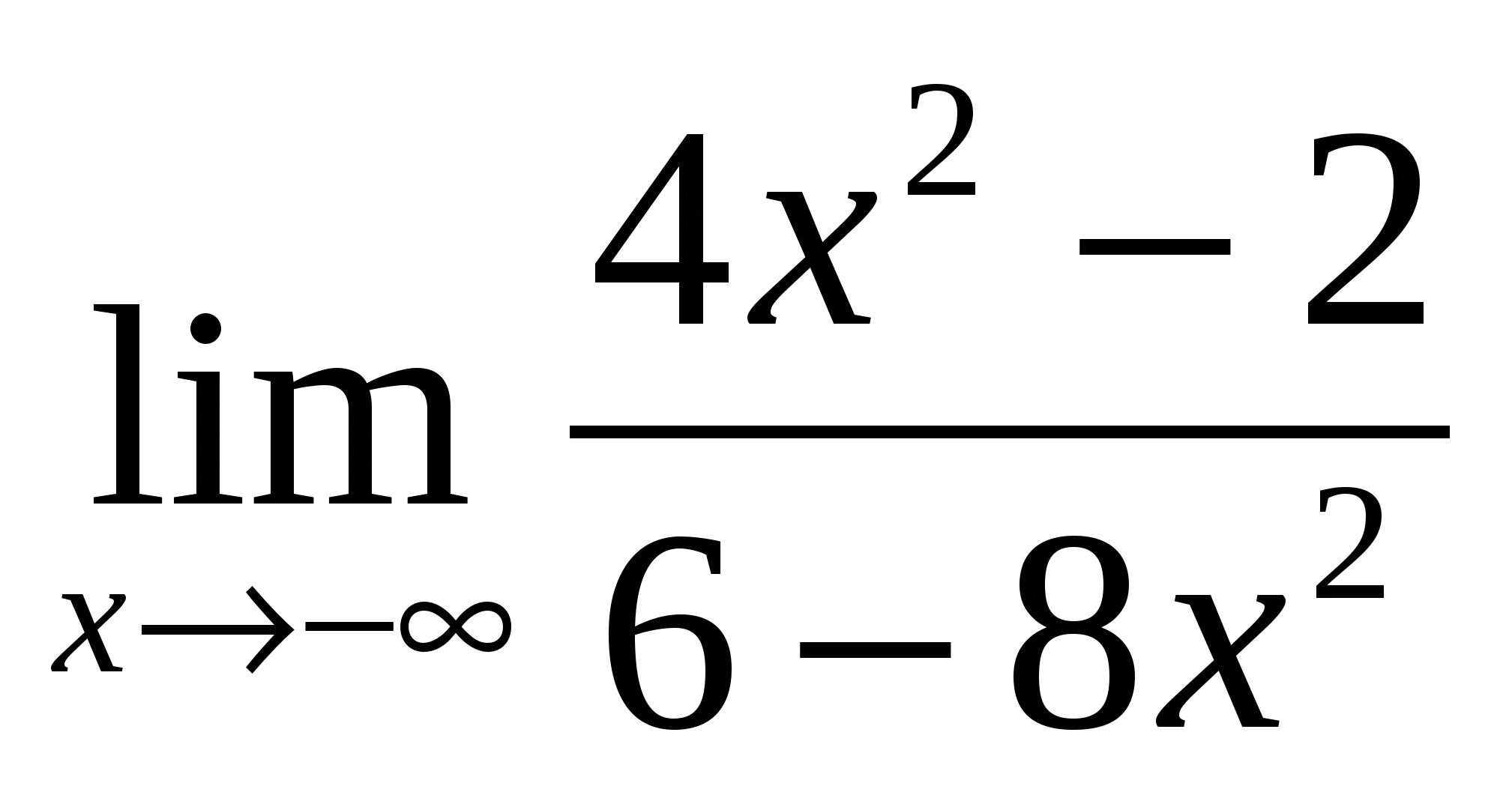
Решение:
Тема: «Производная функции. Дифференциал и его приложение к приближенным вычислениям»
Знания:
определение непрерывности и дифференцируемости функции;
приращение функции, приращение аргумента;
определение производной ее геометрический и механический смысл;
таблицу производных;
определение дифференциала.
Умения:
находить производные элементарных и сложных функций;
вычислять дифференциалы функции;
применение дифференциала к приближённым вычислениям.
Правила дифференцирования
Найдите производную функции 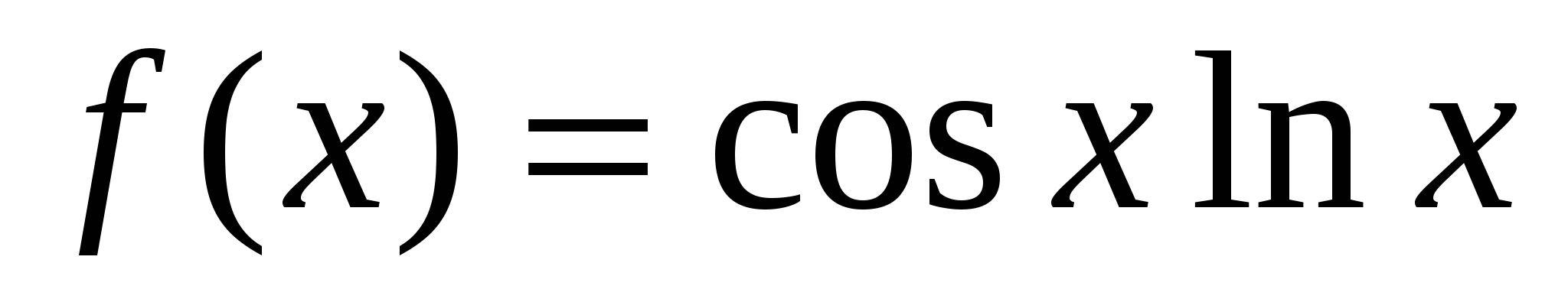
Решение:
Найдите производную сложной функции 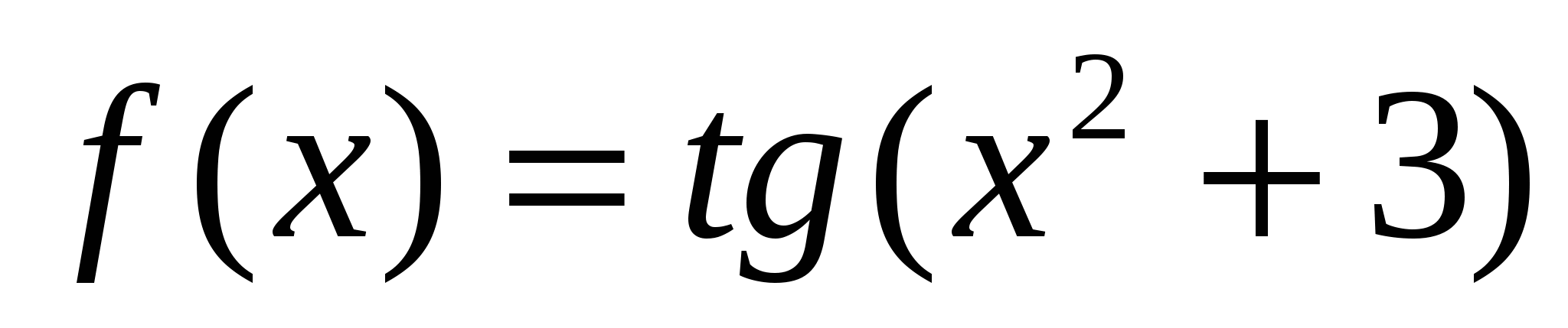
Решение:
Физический и геометрический смысл производной
Смещение в ответ на одиночное мышечное сокращение описывается уравнением 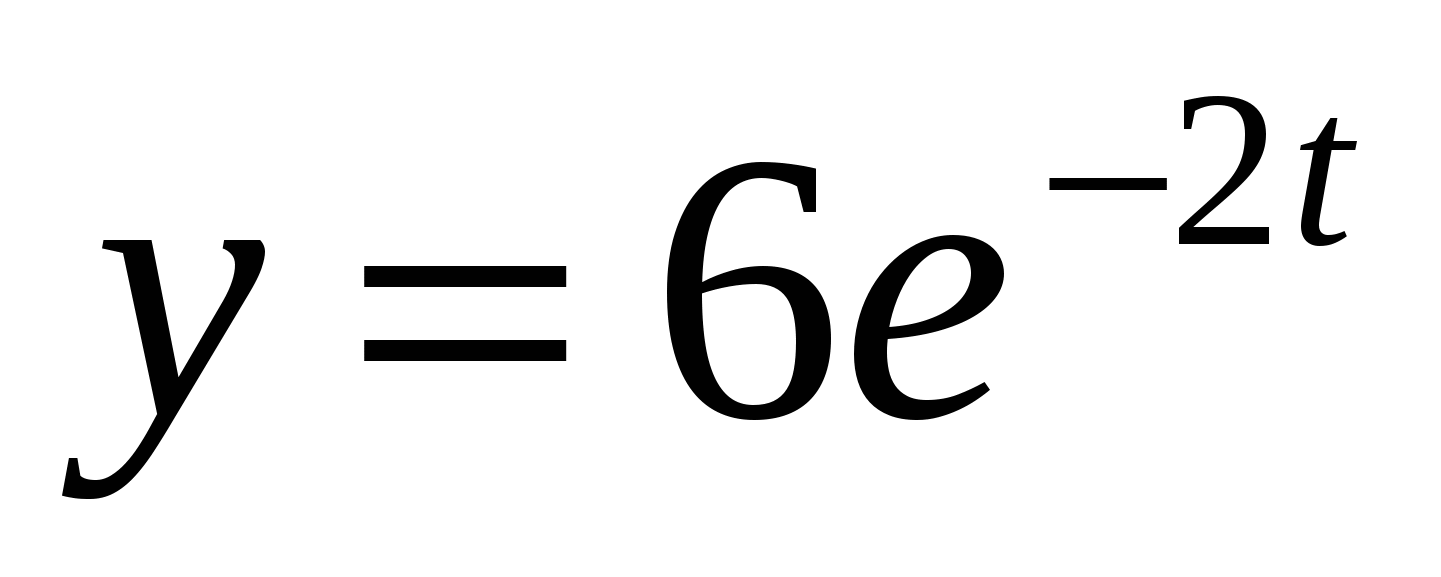 . Определить скорость мышечного сокращения в момент времени t=3 c. . Определить скорость мышечного сокращения в момент времени t=3 c.
Решение:
Напишите уравнение касательной к графику функции 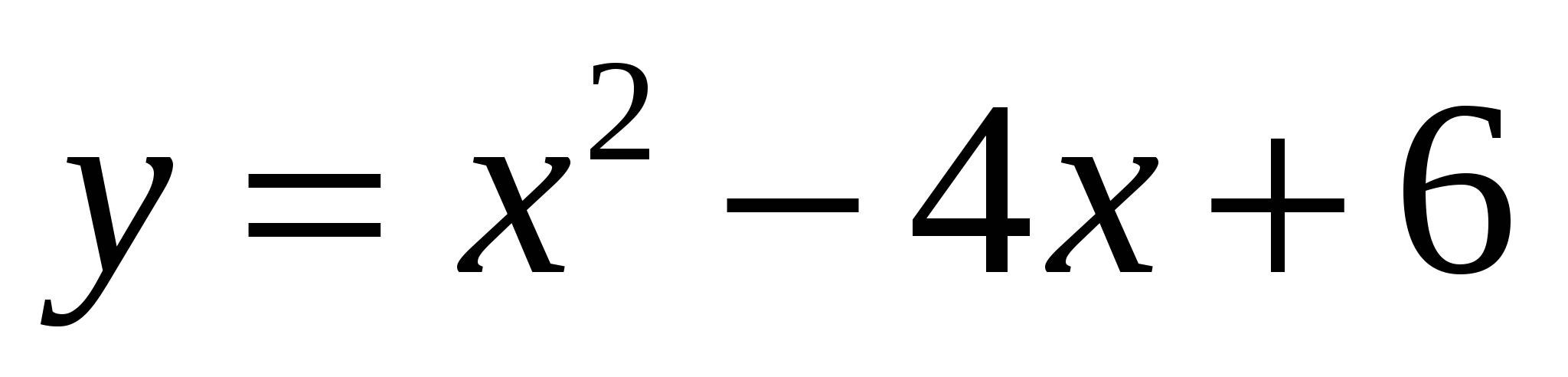 в точке х0=5. в точке х0=5.
Решение:
Применение дифференциала
при приближенных вычислениях
Вычислить приближенно 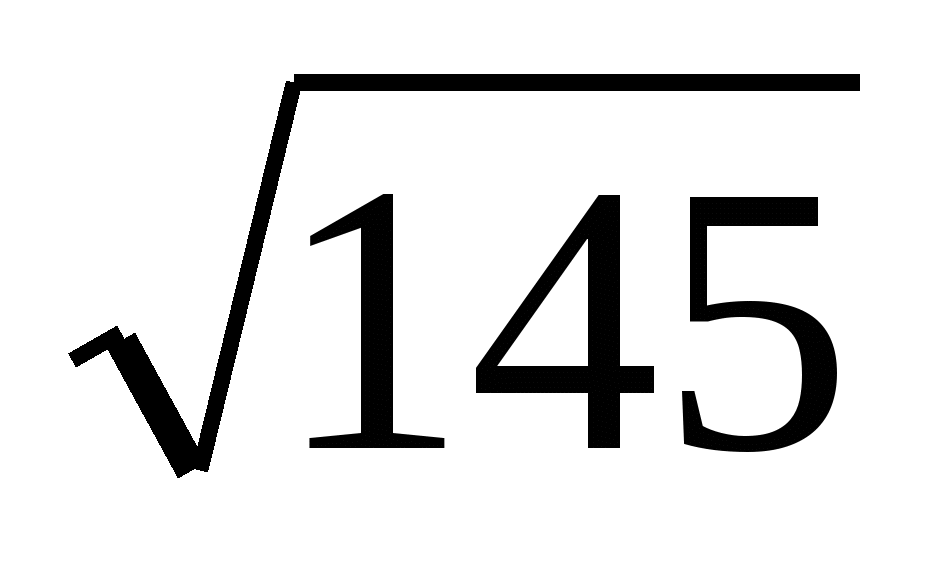
Решение:
Применение производной при исследовании функции и построении её графика
Постройте график функции 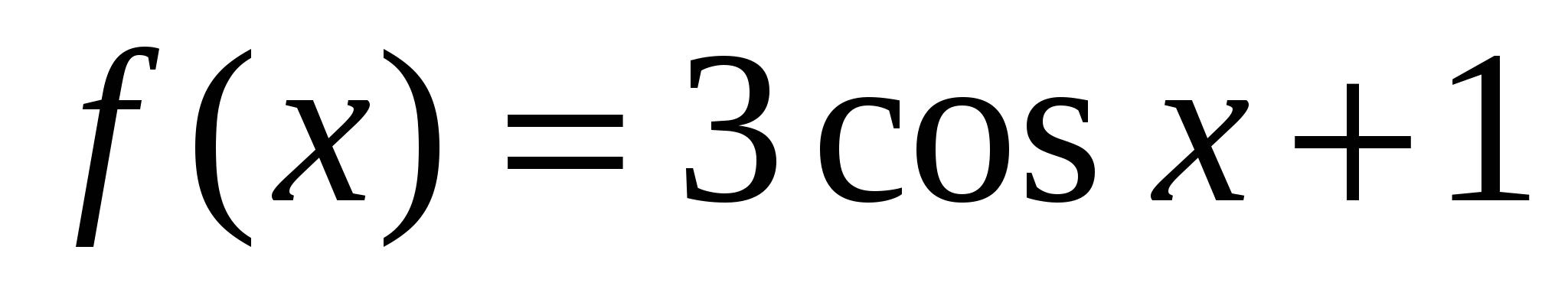
Решение:
Тема: «Неопределенный и определенный интегралы и их свойства.
Применение определенного интеграла к решению прикладных задач»
Знания:
определение первообразной функции;
определение неопределенного интеграла;
свойства неопределенного интеграла;
таблицу неопределенных интегралов;
методы интегрирования;
формулу Ньютона-Лейбница для вычисления определенных интегралов;
методы вычисления определенных интегралов.
Умения:
находить неопределенный интеграл различными методами;
применять формулу Ньютона-Лейбница для вычисления определенного интеграла.
Методы интегрирования
Вычислить интеграл 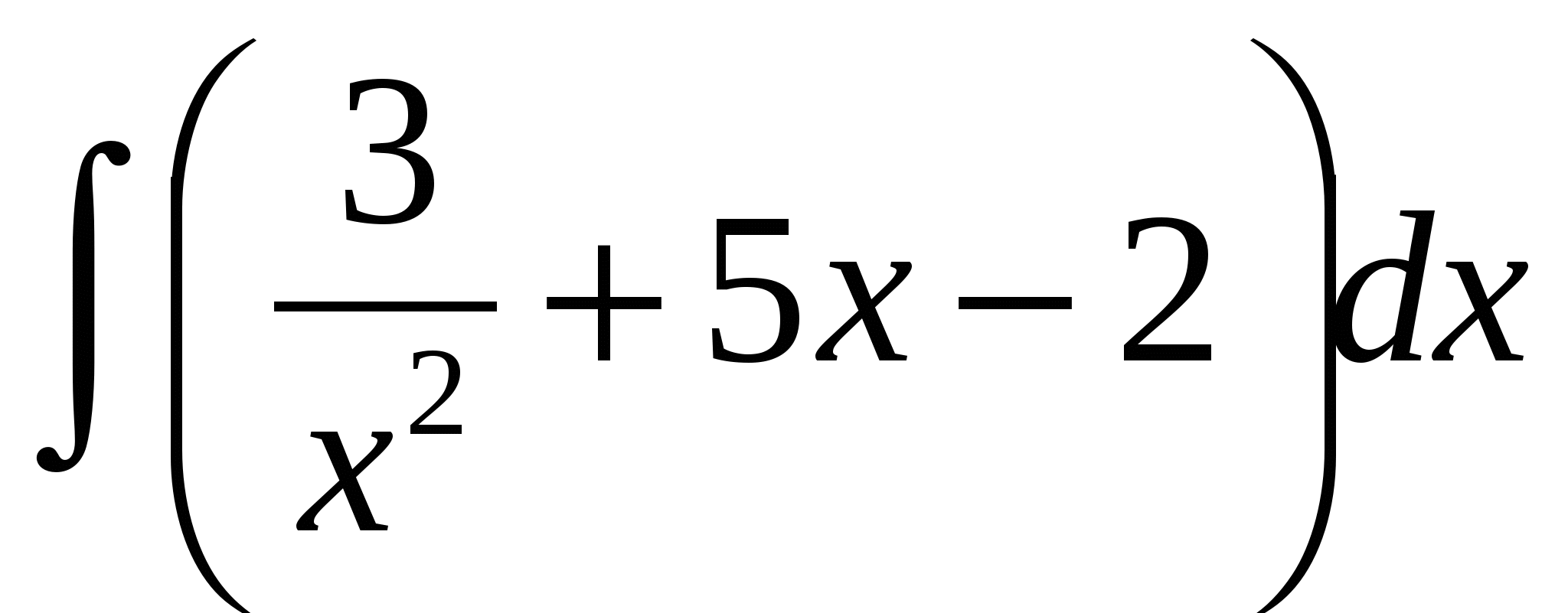 способом непосредственного интегрирования. способом непосредственного интегрирования.
Решение:
Вычислить интеграл 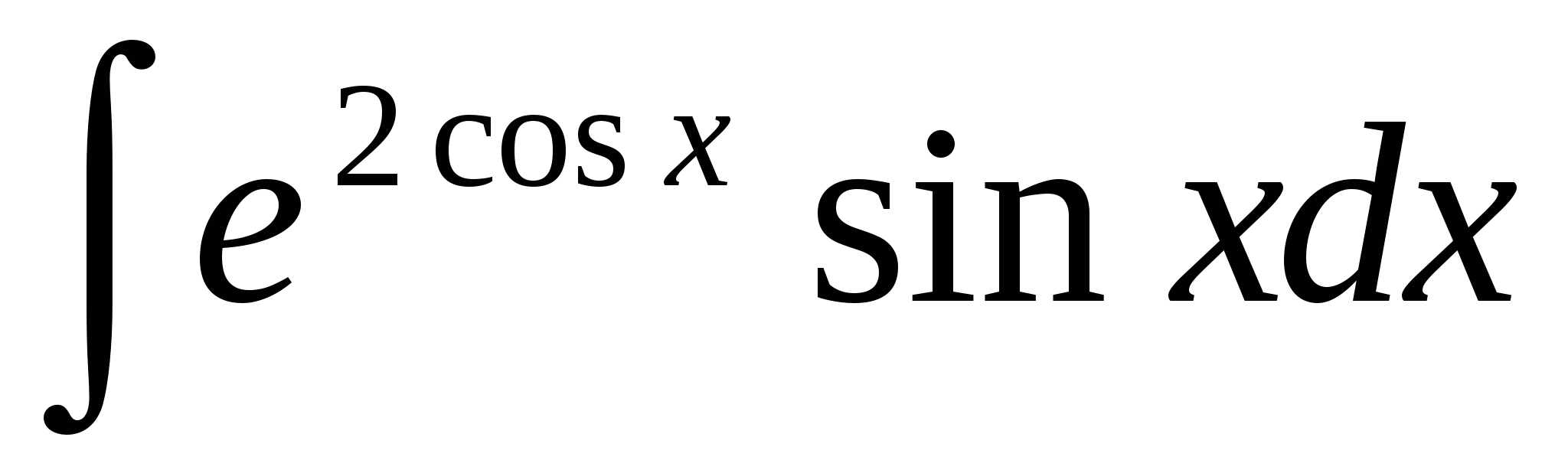 подстановкой. подстановкой.
Решение:
Вычислить интеграл 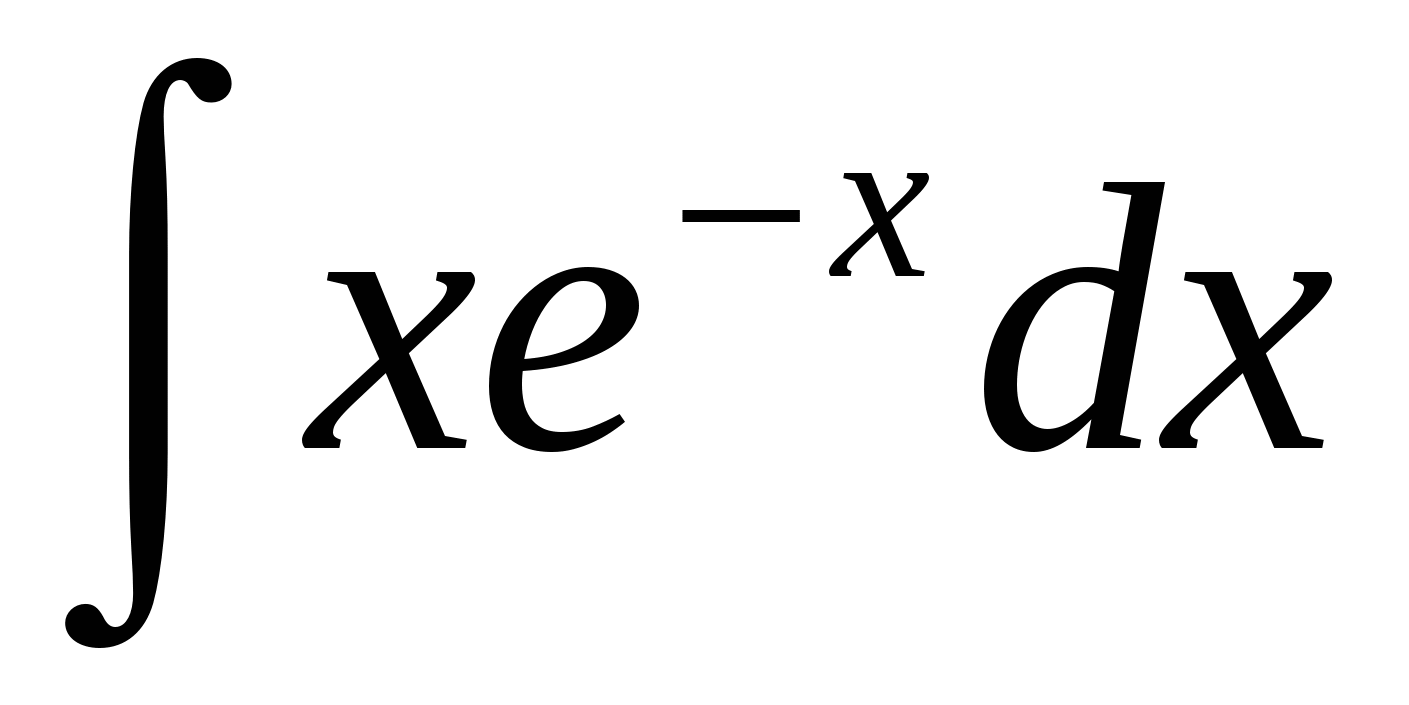 методом интегрирования по частям методом интегрирования по частям
Решение:
Определенный интеграл: Формула Ньютона-Лейбница.
Вычислить определенный интеграл 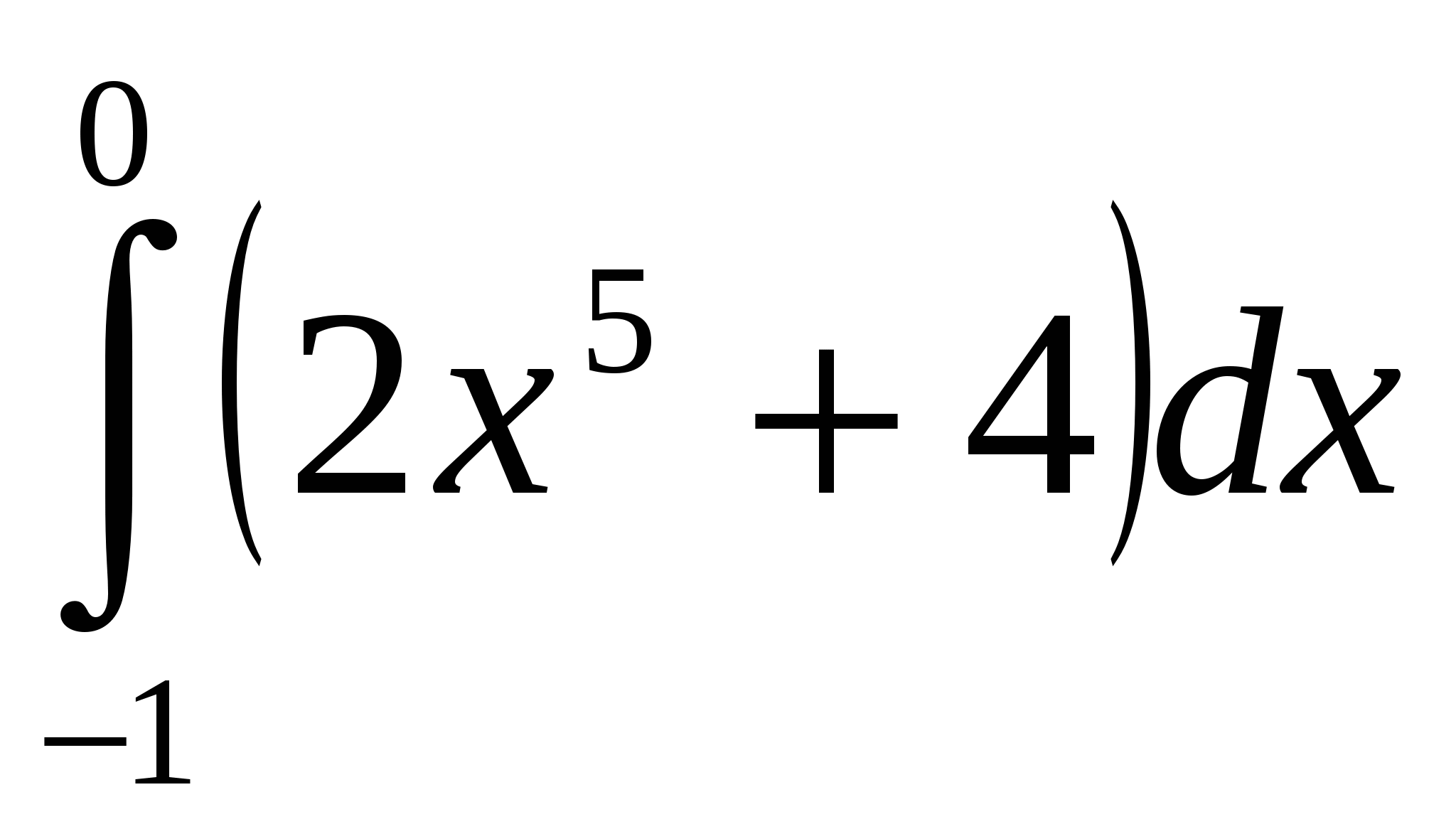
Решение:
Применение определенного интеграла
Найти площадь фигуры, ограниченной осью ОХ и графиком функции 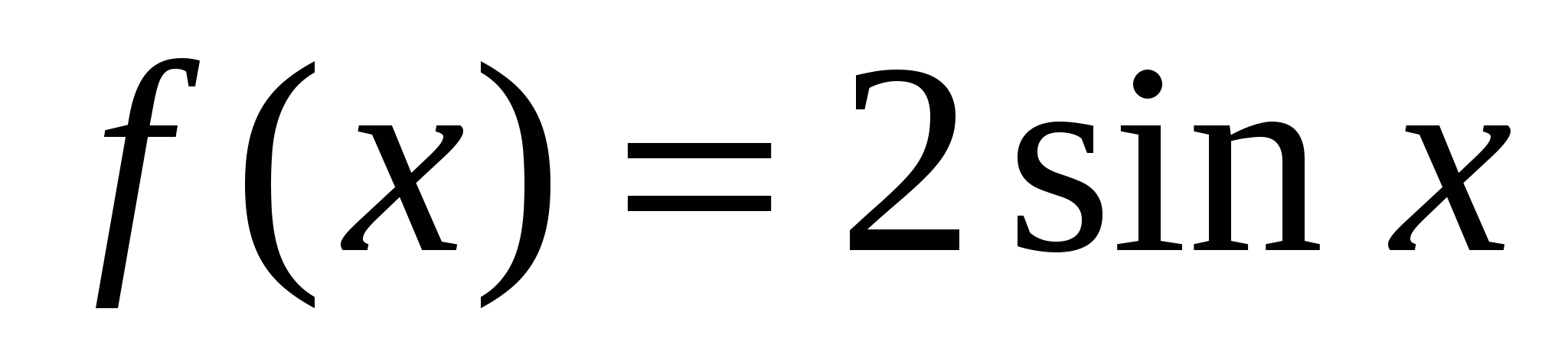 в пределах от 0 до в пределах от 0 до 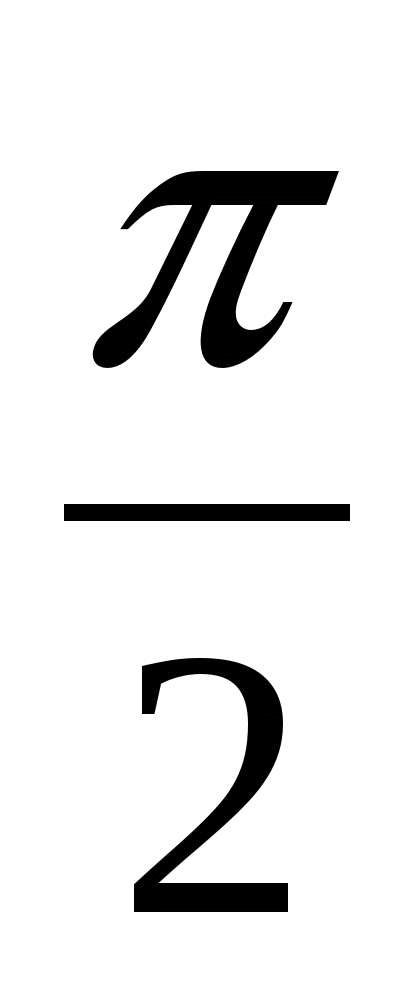 . .
Решение:
Вычислить длину дуги 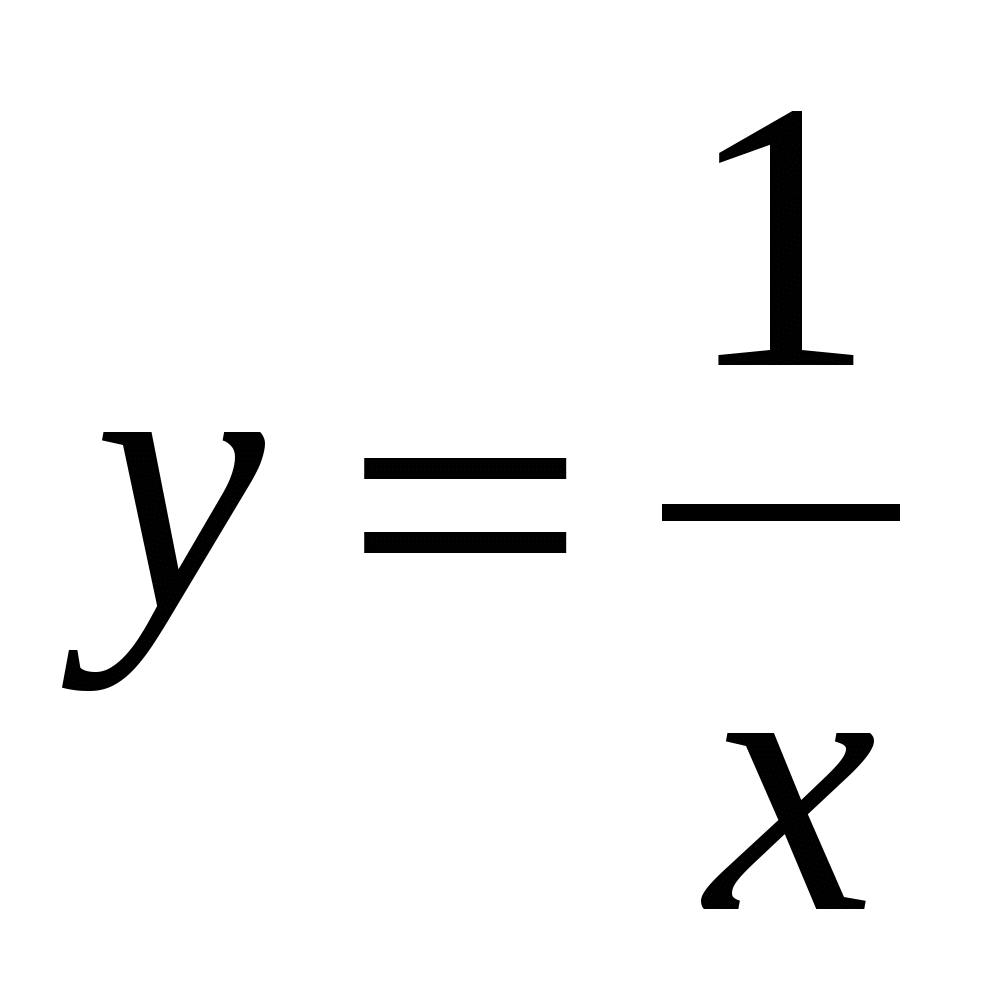 между точками х=2 и х= 4. между точками х=2 и х= 4.
Решение:
Тема: «Дифференциальные уравнения и их применение в медицинской
практике»
Знания:
таблицу неопределенных интегралов;
методы интегрирования;
определение дифференциального уравнения.
Умения:
находить неопределенные интегралы;
составлять и решать дифференциальные уравнения, дифференциальные уравнения с разделяющимися переменными, линейные дифференциальные уравнения первого порядка.
Найти общее решение дифференциального уравнения 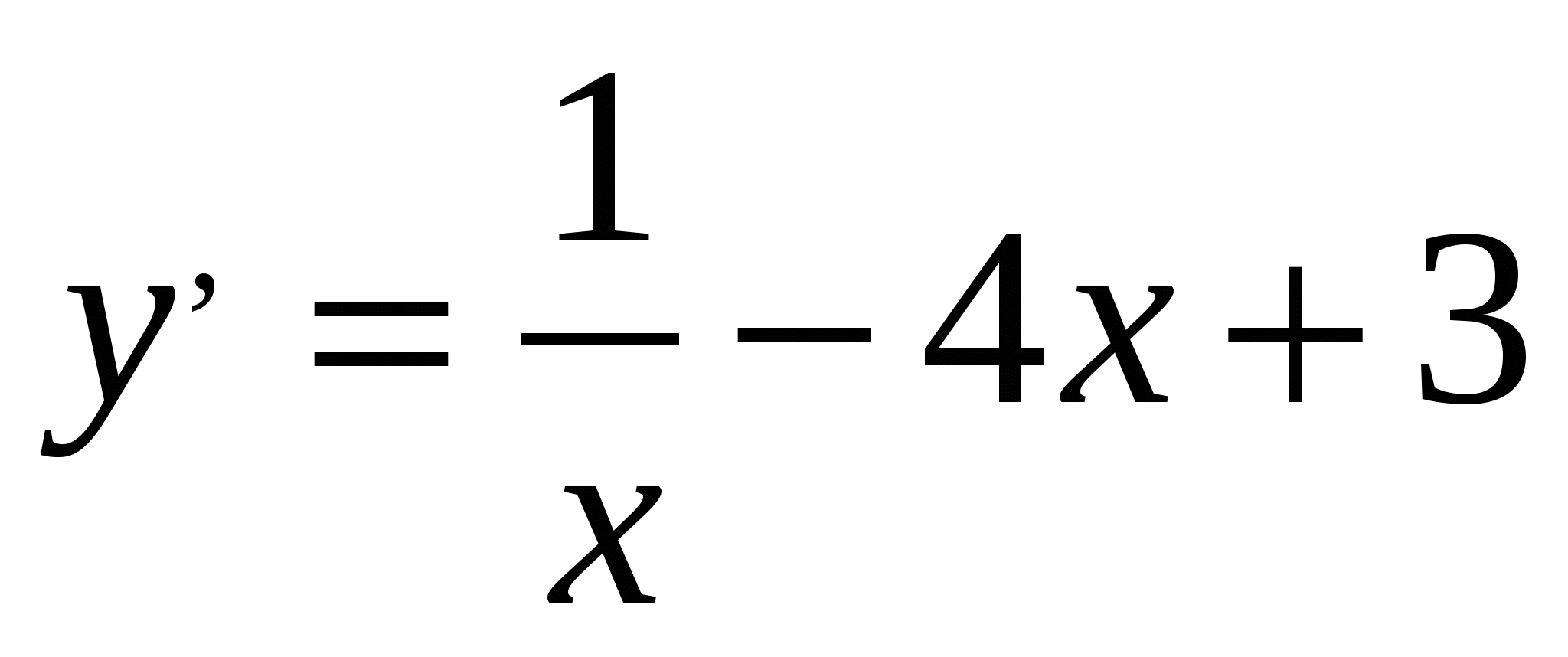
Решение:
Найти частное решение дифференциального уравнения 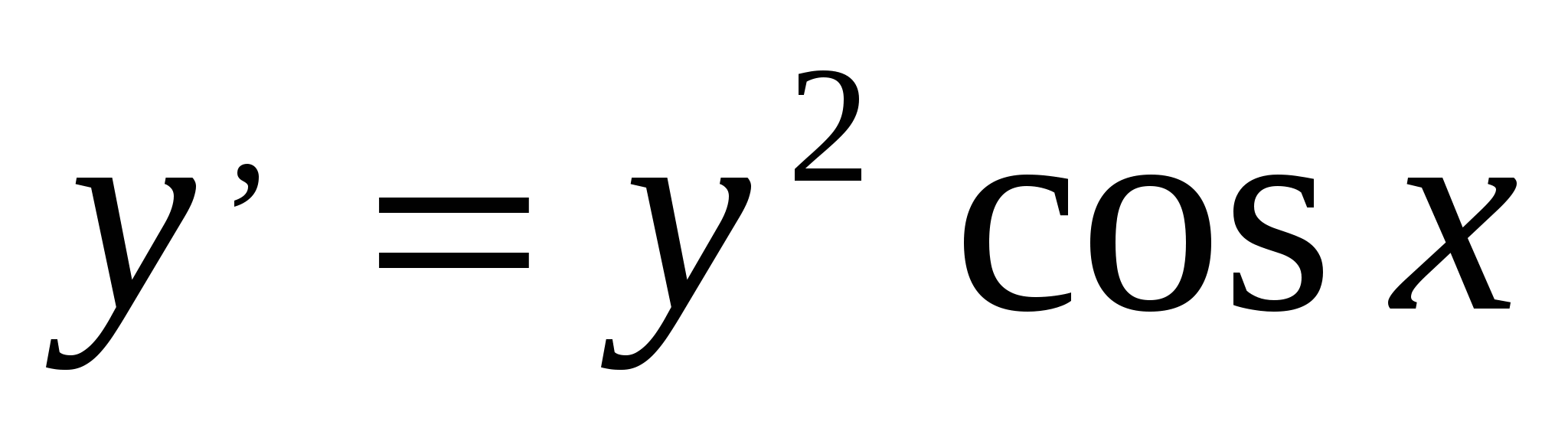 , при y(0)=1 , при y(0)=1
Решение:
Найти общее решение линейного дифференциального уравнения 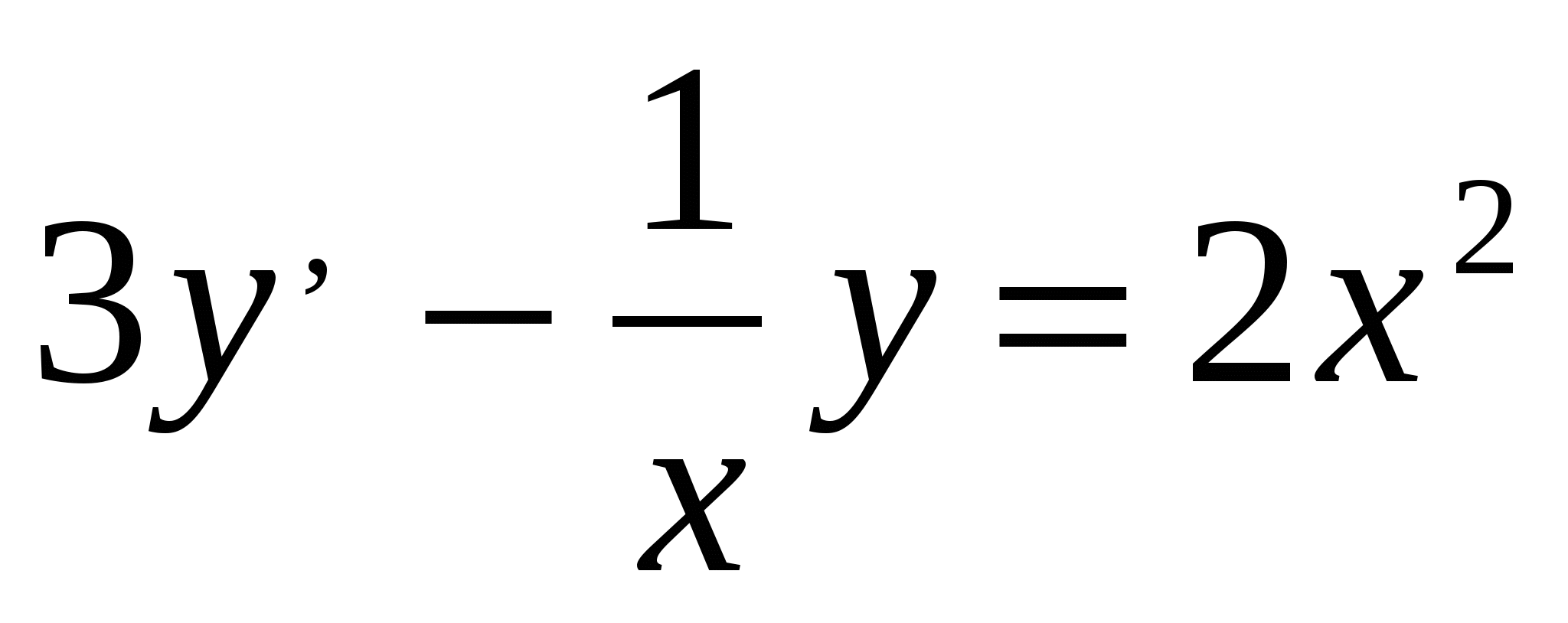
Решение:
Составьте дифференциальное уравнение и найдите частные решения:
Скорость роста микроорганизмов пропорциональна их количеству в данный момент. В начальный момент имелось 100 микроорганизмов, и их число удвоилось за 6 часов.
Решение:
Тема: «Основные понятия дискретной математики. Закон больших чисел. Теория вероятности»
Знания:
элементы математической логики;
основные понятия комбинаторики: размещения, перестановки, сочетания и их формулы;
понятие случайного события, частоты случайного события, достоверности, равносильности, противоположности события;
закон больших чисел;
определение вероятности события;
основные теоремы и формулы теории вероятности;
определение математического ожидания и дисперсии случайной величины.
Умения:
производить операцию дизъюнкций, конъюнкции, отрицания;
находить число размещений, перестановки, сочетания.
находить сумму (объединение), произведение (пересечение) событий, вероятность событий;
применять основные теоремы и формулы при нахождении вероятности события, математического ожидания и дисперсии случайной величины.
Комбинаторика
Вычислите: 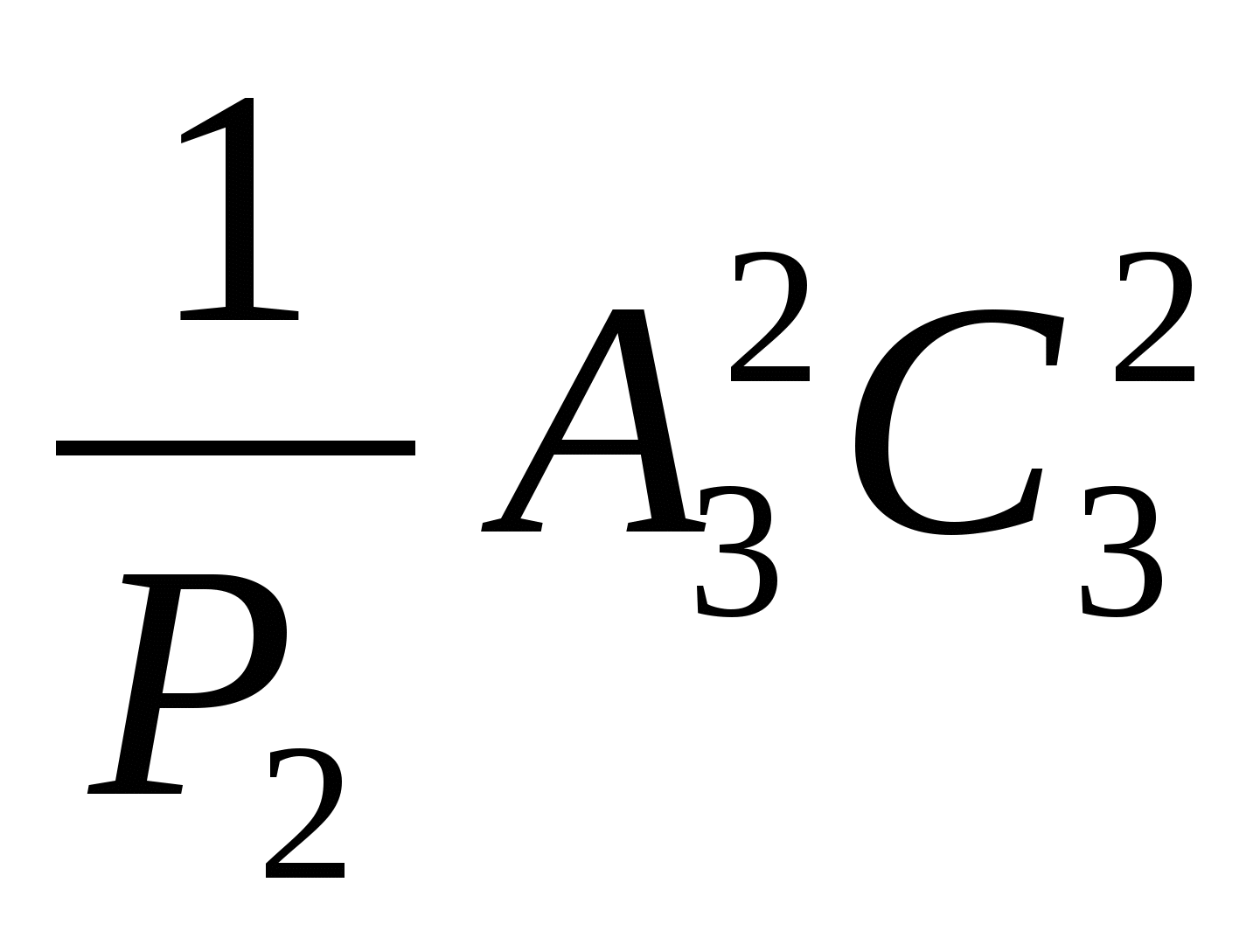
Решение:
Решите задачу:
Имеются 10 ампул, некоторые из них бракованные. Для проверки наугад берут 3 ампулы. Сколькими способами это можно сделать?
Решение:
Теория вероятности. Случайные величины
Случайная величина Х имеет закон распределения:
-
Найдите:
вероятности pi;
математическое ожидание;
дисперсию;
среднее квадратическое отклонение;
постройте многоугольник распределения.
Решение:
среднее квадратическое отклонение:
многоугольник распределения:

Тема: «Математическая статистика и ее роль в медицине и здравоохранении. Медико-демографические показатели»
Знания:
определение статистики;
задачи статистики;
понятие статистической совокупности, единицы измерения, учетные признаки;
этапы статистического исследования, их характеристику.
Умения:
различать структурные элементы статистической совокупности (совокупность, генеральная и выборочная совокупность, единица наблюдения, факторная и результативная признаки);
шифровать учетные признаки;
составлять различные виды таблиц и строить диаграммы.
Практическое применение статистических показателей для вычисления показателей здоровья населения и деятельности ЛПУ.
Ответить письменно на вопросы:
Каким способом проводят перепись населения в России.
(ответ пометьте знаком )
Анкетный
Метод саморегистрации
Экспедиционный (анкеты заполняют специально подготовленные экспедиторы)
Каким способом регистрируются статистические сведения и как организован сбор данных при учете естественного движения населения (рождаемость, смертность)
Ответ: ________________________________________________________
______________________________________________________________
________________________________________________________________
______________________________________________________________
________________________________________________________________
______________________________________________________________
________________________________________________________________
______________________________________________________________
________________________________________________________________
______________________________________________________________
Проведение исследования согласно этапам статистического исследования:
Соберите данные о весе студентов вашей группы. Занесите данные в таблицу, разбив их на две группы: проживающие в сельской местности и проживающие в городской местности. Для каждой группы найдите выборочную среднюю, среднее квадратическое отклонение и ошибку выборочной средней. Сравните результаты, сделайте выводы, постройте столбиковую диаграмму.
Решение:
Тема: «Применение математических методов в профессиональной деятельности среднего медицинского персонала»
№1
Знания:
определение процента;
меры объема;
концентрацию растворов;
понятие пропорций.
Умения:
составлять и решать пропорции;
рассчитывать концентрацию раствора;
получать нужную концентрацию раствора;
Решите задачи:
№ 1.
Сколько вещества необходимо взять для получения раствора 1:3000 – 200 мл.
Решение:
№ 2.
Свежие фрукты содержат 72% воды, а сухие 20%. Сколько сухих фруктов получается из 20 кг свежих?
Решение:
№ 2
Знания:
способы расчета питания;
формулы расчета антропометрических показателей
Умения:
оценивать пропорциональность развития ребенка, используя антропометрические индексы;
вычислять долженствующую длину, массу, окружность груди и головы ребенка в зависимости от возраста;
рассчитывать количество молока объемным и калорийным методами, применять вышеизложенные формулы на практике.
№ 1.
Ребёнку 4 года. Определить какое количество молока он должен получить, если масса тела 16 кг.
Решение:
№ 2.
Галя П. 1 год 9 мес. Масса 10.800, рост 81 см, о.гол 47 см, о.гр 48 см.
Рассчитайте долженствующие антропометрические показатели.
Решение:
|
|
|
 Скачать 172.5 Kb.
Скачать 172.5 Kb.