Работа на уроке Найдите корень уравнения
 Скачать 158.82 Kb.
|
|
Работа на уроке Найдите корень уравнения:  В  среднем из 1400 садовых насосов, поступивших в продажу, 7 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах. Найдите значение выражения  Н 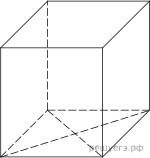 айдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10.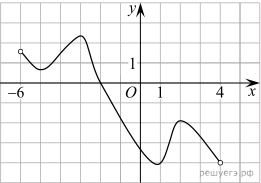 Функция  определена на промежутке  На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция принимает наибольшее значение.Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой  где  м  − постоянные параметры,  − смещение камня по горизонтали,  − высота камня над землeй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды? Н  а рисунке изображён график функции вида  где числа a, b и c — целые. Найдите значение дискриминанта уравнения  .На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Вани есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения? Найдите наименьшее значение функции  на отрезке  а) Решите уравнение  б) Укажите корни этого уравнения, принадлежащие отрезку  В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 12 и  Длины боковых рёбер пирамиды SA = 5, SB = 13, SD = 10.а) Докажите, что SA — высота пирамиды. б) Найдите расстояние от вершины A до плоскости SBC. Домашняя работа 1. Найдите корень уравнения:  2  . Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.3. В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах. Найдите значение выражения   Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760. 6  .Функция y = f (x) определена и непрерывна на отрезке [−5; 5]. На рисунке изображён график её производной. Найдите точку x0, в которой функция принимает наименьшее значение, если f (−5) ≥ f (5). 7. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону  где  − начальный уровень воды,  м/мин2, и  м/мин постоянные, t − время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.8. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго? 9 На рисунке изображён график функции вида где числа a, b и c — целые. Найдите значение  .10. Шоколадка стоит 35 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Какое наибольшее количество шоколадок можно получить, потратив не более 200 рублей в воскресенье? 11. Найдите наибольшее значение функции  на отрезке  12 а) Решите уравнение  б) Укажите корни этого уравнения, принадлежащие отрезку  13. Дана пирамида SABC, в которой   а) Докажите, что ребро SA перпендикулярно ребру BC. б) Найдите расстояние между ребрами BC и SA. |