ЭCбз-21-1 76 Матаевский С.К.. Работы Индивидуальное задание вариант 76. Номер варианта по дисциплине Прикладная физика в электроэнергетике Наименование учебной дисциплины

• Название: Работы Индивидуальное задание вариант 76. Номер варианта по дисциплине Прикладная физика в электроэнергетике Наименование учебной дисциплины
• Дата: 10.01.2023
• Размер: 0.9 Mb.
• Имя файла: ЭCбз-21-1 76 Матаевский С.К..docx
• Тип: Документы; #879409
• страница: 11 из 15

6. Работа по перемещению проводника с током в магнитном поле. Электромагнитная индукция. Индуктивность

Основные формулы

• Работа по перемещению замкнутого контура с током в магнитном поле

A = IФ,

где Ф – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром; I – сила тока в контуре.

• Основной закон электромагнитной индукции (закон Ленца)



где Ɛ_i – электродвижущая сила индукции; N — число витков контура;  – потокосцепление.

Частные случаи применения основного закона электромагнитной индукции:

а) разность потенциалов U на концах проводника длиной I, движущегося со скоростью  в однородном магнитном поле,

U = Blsin,

где  – угол между направлениями векторов скорости  и магнитной индукции В;

б) электродвижущая сила индукции Ɛ_i, возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью со в однородном магнитном поле с индукцией В



где t – мгновенное значение угла между вектором В и вектором нормали n к плоскости рамки.

• Количество электричества Q, протекающего в контуре,



где R — сопротивление контура;  – изменение потокосцепления.

•Электродвижущая сила самоиндукции Ɛ_i,возникающая в замкнутом контуре при изменении силы тока в нем,



где L — индуктивность контура;

<Ɛ> – означает приближённое значение электродвижущей силы Ɛ, когда точное значение производной dI/dt заменяют приближённым I/t, основанным на разности измеренных значений токов и разности соответствующих значений времени, в которые производились измерения.

• Потокосцепление контура  = LI, где L — индуктивность контура.

• Индуктивность L соленоида (тороида) длиной l равна

L = μ₀μ N²S/l,

где N – число витков соленоида; S – площадь поперечного сечения.

Во всех случаях вычисления индуктивности соленоида (тороида) с сердечником по приведённой формуле для определения магнитной проницаемости следует пользоваться графиком зависимости В от Н (см. рис. 5.1), а затем формулой



• Мгновенное значение силы тока I в цепи, обладающей активным сопротивлением R и индуктивностью L:

а) после замыкания цепи



–ЭДС источника тока; t—время, прошедшее после замыкания цепи;

б) после размыкания цепи



где l₀ – сила тока в цепи при t = 0, t— время, прошедшее с момента размыкания цепи.
Примеры решения задач

Пример 6.1. Виток, по которому течёт ток I = 20 А, свободно установится в однородном магнитном поле В = 16 мТл. Диаметр d витка равен 10 см. Какую работу нужно совершать, чтобы медленно повернуть виток на угол  = /2 относительно оси, совпадающей с диаметром?

Решение. При медленном повороте контура в магнитном поле индукционными токами можно пренебречь и считать ток в контуре неизменным. Работа сил А поля в этом случае определяется выражением

А = I (Ф₂ – Ф₁),

где Ф₁ и Ф₂ – магнитные потоки, пронизывающие контур в начальном и конечном положениях.

Работа внешних сил будет равна модулю работе сил поля и противоположна ей по знаку, т. е.

А = I (Ф₁ – Ф₂). (1)

Так как в начальном положении контур установился свободно (положение устойчивого равновесия), то момент внешних сил, действующий на контур, равен нулю. В этом положении вектор магнитного момента p_m контура сонаправлен с вектором В (рис. 6.1, а) и магнитный поток Ф₁ максимален ( = 0, cos  = 1), т. е. Ф₁ = ВS (где S – площадь контура). В конечном положении (рис. 6.1, б) вектор p_m перпендикулярен вектору B ( = /2, cos  = 0) и магнитный поток Ф₂ = 0. Перепишем выражение (1) с учётом сделанных замечаний: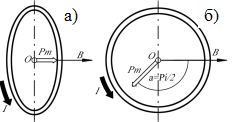




Рис. 6.1


Так как площадь контура S = d²/4. то работа



Убедимся в том, что правая часть равенства дает единицу работы (Дж):



Произведём вычисления:


Пример 6.2. В однородном магнитном поле с индукцией B = 0,1 Тл равномерно вращается рамка, содержащая N = 1000 витков, с частотой вращения n = l0 c^-1. Площадь S рамки равна 150 см². Определить мгновенное значение ЭДС ξ, соответствующее углу поворота рамки 30°.

Решение. Мгновенное значение ЭДС индукции ξ, определяется основным уравнением электромагнитной индукции Ленца: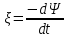

. ξ = -dΨ/dt. (1)

Потокосцепление  = NФ, где N — число витков, пронизываемых магнитным потоком Ф. Подставив выражение  в формулу (1), получим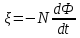

(2)

При вращении рамки магнитный поток Ф, пронизывающий рамку в момент времени t, изменяется по закону Ф = ВS cos t, где В — магнитная индукция; S – площадь рамки; – угловая частота. Подставив в формулу (2) выражение Ф и продифференцировав по времени, найдём мгновенное значение ЭДС индукции:

ξ = N B S ω sin⁡ωt (3)

Угловая частота со связана с частотой п вращения соотношением  = 2п. Подставив выражение со в формулу (3) и заменив t на угол , получим

ξ = 2π n N B S sin α. (4)

Убедимся в том, что правая часть полученного равенства дает единицу измерения ЭДС (В). Учтя, что 2 , N и sin t — величины безразмерные и неименованные, получим



Значение аргумента α равного 30° в функции sin, то есть в формуле (4) требуется вычислить sin 30°.

Произведя вычисления по формуле (4), найдём

ξ = 47,1 В.
Пример. 6.3 По соленоиду течёт ток I = 2 А. Магнитный поток Ф, пронизывающий поперечное сечение соленоида, равен 4 мкВб. Определить индуктивность L соленоида, если он имеет N = 800 витков.

Решение. Индуктивность L соленоида связана с потокосцеплением  соотношением  = LI, откуда L = /I. Заменив здесь потокосцепление  его выражением через магнитный поток Ф и число витков N соленоида ( = ФN), получим

L = ФN /I (1)

Произведя вычисления по формуле (1), получим

L = 1,6 мГн.
Задача 6.1

Вариант №	Ток I, А	В, мТл	d, см
1	21,3	17,5	11,3
2	24,4	20,4	10,4
3	23,7	17	11,7
4	23,3	19,9	10,8
5	23,5	17,2	10,8
6	23,9	21	11,6
7	20,5	16,3	10,9
8	20,4	22	11,9
9	21,2	17,5	11,5
10	23,9	16,4	10,3
11	21,2	17,6	10,6
12	23,9	16,8	10,1
13	20,8	19,9	10,2
14	21,7	16,9	11,8
15	22,5	18,1	11,7
16	23,4	19,1	11,7
17	23,2	19,7	10,3
18	20,7	20,9	11,6
19	22	16,9	10,1
20	23,3	18,8	11,1
21	23,4	16,5	10,5
22	24,3	16,5	10,7
23	20,3	21,5	10,4
24	21	20,1	11,9
25	24,9	16,3	12
26	20,1	21,4	11,5
27	25	18,2	10,2
28	23	17,5	10,3
29	21,9	21,3	11,1
30	23,6	16,5	11,3
31	21,2	16,4	10,7
32	24	20,5	10,2
33	23,5	17,1	12
34	21,7	20,2	11,2
35	22,2	17,9	11,4
36	22,1	16,8	11,2
37	23,2	21,9	10,7
38	20,6	18,2	11,1
39	23,1	17,7	11,4
40	22,5	18,2	10,1
41	22,1	17,2	11,2
42	23,1	21,3	11,3
43	20,5	17	10
44	23,4	17,4	10,7
45	21,2	17,2	10,5
46	22,9	17,1	12
47	20,5	17,1	11,6
48	24,1	16,1	11,5
49	21,2	19,2	11,1
50	23,3	20,7	11,1
51	20,8	16,2	10,4
52	23,3	17,8	10,3
53	24,2	17,7	11
54	23,5	21,8	10,5
55	21,7	19,9	11,5
56	24,5	19	10,9
57	20,1	18,2	10,7
58	22,6	21,9	11,8
59	20,3	20,9	10,7
60	23,9	17,2	11,6
61	20,1	17	10,7
62	23,4	19,3	10,2
63	22,4	20,2	10,9
64	21,7	16,2	11,5
65	20,2	21,2	10,5
66	24,6	16,8	10
67	22,6	21,5	11,8
68	24,2	16,9	11,7
69	23	18,6	11,2
70	23,2	16,8	11,3
71	24,4	17,8	11,3
72	20,2	20,6	11,2
73	21,7	18,8	11,2
74	22,9	19,4	11,1
75	23,5	17,7	10,6
76	20,2	19,4	10,8
77	20,4	16,3	10,9
78	20,6	18,5	12
79	23,3	20,5	12
80	20	19,6	11,4
81	21,8	18,3	11,3
82	21,9	21,5	11,1
83	23,7	17,5	10,5
84	20,7	21,5	11,9
85	22,4	20,7	11,2
86	23,7	21,9	11,8
87	22,7	21,3	11,1
88	24,3	21,4	11,3
89	24,2	17,9	10,5
90	22,7	21,9	11,4
91	22,6	18,9	11,9
92	24,7	19,9	11,7
93	20,1	18,4	10,3
94	23,5	16,4	11,1
95	24,9	21	10,1
96	21,6	20,7	10,2
97	21,9	17,8	10,8
98	20,5	21	11,1
99	22,7	16,4	10,7
100	20,1	18,7	11,4