ЭCбз-21-1 76 Матаевский С.К.. Работы Индивидуальное задание вариант 76. Номер варианта по дисциплине Прикладная физика в электроэнергетике Наименование учебной дисциплины
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
5. Закон полного тока. Магнитный поток. Магнитные цепиОсновные формулы Циркуляция вектора магнитной индукции В вдоль замкнутого контура 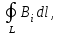 где Bi — проекция вектора магнитной индукции на направление элементарного перемещения dl вдоль контура L. Циркуляция вектора напряжённости Н вдоль замкнутого контура 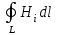 , , Закон полного тока (для магнитного поля в вакууме) 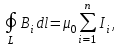 где 0 – магнитная постоянная; 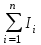 — алгебраическая сумма токов, охватываемых контуром; п — число токов. — алгебраическая сумма токов, охватываемых контуром; п — число токов.Закон полного тока (для произвольной среды) 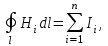 Магнитный поток Ф через плоский контур площадью S: а) в случае однородного поля Ф = BScos ; или Ф = BnS, где – угол между вектором нормали n к плоскости контура и вектором магнитной индукции В; Вn — проекция вектора В на нормаль n (Bn = B cos ); б) в случае неоднородного поля 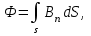 где интегрирование ведется во всей поверхности S. Потокосцепление, т.е. полный магнитный поток, сцепленный со всеми витками соленоида или тороида, 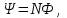 где Ф – магнитный поток через один виток; N — число витков соленоида или тороида. Магнитное поле тороида, сердечник которого составлен из двух частей, изготовленных из веществ с различными магнитными проницаемостями: а) магнитная индукция на осевой линии тороида 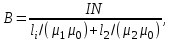 где I – сила тока в обмотке тороида; N — число ее витков; l1 и l2 - длины первой и второй частей сердечника тороида; 1 и 2 –магнитные проницаемости веществ первой и второй частей сердечника тороида; 0 –магнитная постоянная (0 = 4 107); б) напряжённость магнитного поля на осевой линии тороида в первой и второй частях сердечника H1 = B /(1 2); H1 = B /(2 0 ); в) магнитный поток в сердечнике тороида площадью S 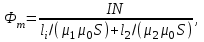 или по аналогии с законом академика Петрова-Ома Фm = Fm/Rm, где Fm – магнитодвижущая сила; Rm — полное магнитное сопротивление цепи;  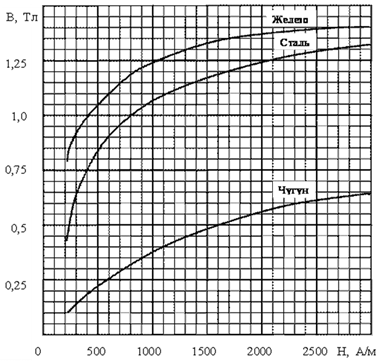 Рис. 5.1. г) магнитное сопротивление участка цепи Rm = l/(μμ0S). • Магнитная проницаемость μ, ферромагнетика связана с магнитной индукцией В поля в нем и напряжённостью Н намагничивающего поля соотношением: μ = B/(μ0H). • Связь между магнитной индукцией В поля в ферромагнетике и напряжённостью Н намагничивающего поля для трёх материалов (железо, сталь, чугун) имеет нелинейный характер и графически показана на рис. 5.1. Примеры решения задач Пример 5.1. В одной плоскости с бесконечно длинным прямым проводом, по которому течёт токI = 50 А, расположена прямоугольная рамка так, что две большие стороны ее длиной l= 65 см параллельны проводу, а расстояние от провода до ближайшей из этих сторон равно ее ширине. Каков магнитный поток Ф, пронизывающий рамку? Решение. Магнитный поток Ф через поверхность площадью S определяется выражением 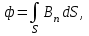 (1) (1)где Вn – вектор магнитной индукции перпендикулярный плоскости рамки.  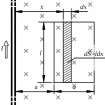 Рис. 5.2 Рис. 5.2В нашем случае вектор магнитной индукции Вn перпендикулярен плоскости рамки, по правилу буравчика магнитные силовые линии идут от нас. Поэтому для всех точек рамки синус равен единице, значит Вn = В. Магнитная индукция В, создаваемая бесконечно длинным прямым проводником с током, определяется формулой 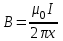 , (2) , (2)где x– расстояние от провода до точки, в которой определяется В. Для вычисления магнитного потока заметим, что так как В согласно (2) зависит от х, то и элементарный поток Ф будет также зависеть от х. Для приращений из выражения (1) имеем: dФ = B(x)dS. Разобьём площадь рамки на узкие элементарные площадки длиной l, шириной dx и площадью dS = ldx (рис. 5.2). В пределах этой площадки магнитную индукцию можно считать постоянной, так как все части площадки равноудалены (на расстояние х) от провода. С учётом сделанных замечаний элементарный магнитный поток можно записать в виде dФ = 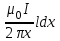 . (3) . (3)Из условия задачи известно, расстояние от провода с током до ближайшей из сторон рамки равно ширине рамки. Обозначим это расстояние через а. Теперь интегрировать выражение (3) нужно в пределах от a до 2а, выполнив интегрирование найдём 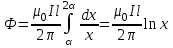 |а2а. |а2а.Подставив пределы и учитывая, что ln 2a – lna = ln (2a/a) = ln 2, получим 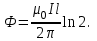 (4) (4)Убедимся в том, что правая часть полученного равенства (4) даёт единицу магнитного потока (Вб): [0] [I] [l] = Гн/м 1 А 1 м=1 Вб. Произведя вычисления с исходными данными по формуле (4), найдём значение магнитного потока: Ф = 4,5 мкВб. Пример 5.2. Определить индукцию В и напряжённость Н магнитного поля на оси тороида (бублика) без сердечника, по обмотке которого, содержащей N = 200 витков, идёт ток I = 5 А. Внешний диаметр d1тороида равен 30 см, внутренний d2 = 20 см. Решение. Для определения напряжённости магнитного поля внутри тороида вычислим циркуляцию вектора Н вдоль линии магнитной индукции поля: 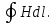 Из условия симметрии следует, что линии магнитной индукции тороида представляют собой окружности и напряжённости во всех точках этой линии одинаковы. Поэтому в выражении циркуляции напряжённость Н можно вынести за знак интеграла, а интегрирование проводить в пределах от нуля до 2 r, где r — радиус окружности, совпадающей с линией индукции, вдоль которой вычисляется циркуляция, т. e. 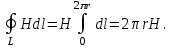 (1) (1)С другой стороны, в соответствии с законом полного тока циркуляция вектора напряжённости магнитного поля равна сумме токов N, охватываемых контуром, вдоль которого вычисляется циркуляция: 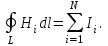 (2) (2)Приравняв правые части равенств (1) и (2), получим 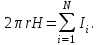 (3) (3)Линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому формула (3) примет вид 2rH = NI, откуда 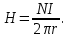 (4) (4)Для средней линии тороида r = (R1+R2)/2 = (d1+d2)/4. Подставив это выражение для r в формулу (4), найдём 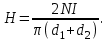 (5) (5)Магнитная индукция В0в вакууме связана с напряжённостью поля соотношением B0 = 0H. Следовательно, 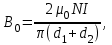 (6) (6)Подставив значения величин в выражения (5) и (6), получим: H = 1,27 кА/м, B0 = 1,6 мТл. Пример. 5.3. Чугунное кольцо имеет воздушный зазор длиной lо = 5 мм. Длина l средней линии кольца равна 1 м. Сколько витков N содержит обмотка на кольце, если при силе тока I = 4 А индукция В магнитного поля в воздушном зазоре равна 0,2 Тл? Рассеянием магнитного потока в воздушном зазоре можно пренебречь. Явление гистерезиса не учитывать. Решение. Пренебрегая рассеянием магнитного потока, мы можем принять, что индукция поля в воздушном зазоре равна индукции поля в чугуне. На основании закона полного тока запишем IN = Hl+H0I0. По графику (см. рис. 5.1) находим, что при В = 0,2 Тл напряжённость Н магнитного поля в чугуне равна 450 кА/м. Так как для воздуха = 1, то напряжённость поля в воздушном зазоре при 0 = 4 10-7 равна H0 = B/0 =B/(4π) = 159155 A/м или 159,155 кA/м. Искомое число витков N = (Hl+H0lo)/I = 131,5 т.е 132 витка. Задача 5.1
|
