Расчет характеристик функций распределения случайной величины
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Некоммерческое акционерное сообщество «АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»  Кафедра «Автоматизация и управление» ОТЧЕТ Лабораторная работа №6. По дисциплине: Математические основы автоматики. Тема: Расчет характеристик функций распределения случайной величины. Специальность: Автоматизация и управление. Выполнила: Кечин Вячеслав Группа: АУу-22-4 Приняла: Ибраева Л ___________ ____________ «_____» __________2022 г. (оценка) (подпись) Алматы 2022 г. Лабораторная работа №6. Расчет характеристик функций распределения случайной величины. Цель работы: изучить функции распределения и методику расчета основных характеристик. 6.1 Задание на лабораторную работу В процессе выполнения лабораторной работы студент должен: - изучить основные понятия теории случайных величин; - изучить числовые характеристики случайных величин, формулы их вычисления; - выполнить задания к лабораторной работе по приведенным формулам и с помощью систем MatLab и MathCAD; - выполнить анализ результатов. 6.2 Основные определения, законы распределения случайных величин Случайной величиной (СВ) называют такую величину, которая в результате опыта может принимать те или иные значения, причем до опыта мы не можем сказать какое именно значение она примет. Случайные величины обозначаются последними буквами латинского алфавита – X,Y,Z. Случайные величины могут быть дискретные и непрерывные, Дискретная случайная величина (ДСВ) может принимать конечное число значений. Пусть Х - дискретная случайная величина, которая принимает значения: x1, x2, …,xn,… с вероятностями рi , где i = 1, 2, …, n,… Значения xi и соответствующие рi представляют в виде таблицы: 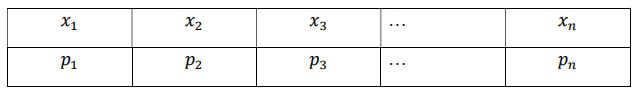 Эта таблица является одной из форм задания ДСВ. Обычно случайные величины располагаются в возрастающем порядке. Основное свойство таблицы заключено в том, что сумма вероятностей равна 1: Непрерывная случайная величина (НСВ) в отличие от ДСВ принимает бесконечное несчетное число значений. Непрерывная случайная величина (НСВ) в отличие от ДСВ принимает бесконечное несчетное число значений. Числовые характеристики дискретных случайных величин. На практике нет необходимости характеризовать случайную величину полностью. Обычно достаточно указать только отдельные числовые параметры распределения. Такие числовые параметры принято называть числовыми характеристиками распределения. Математическим ожиданием M(X) дискретной случайной величины X называется величина: То есть, M(X) - это сумма парных произведений случайной величины на соответствующую вероятность. Мода Mо(X) распределения – это значение СВ, имеющее наиболее вероятное значение. Медиана Me(X) – это значение случайной величины, которое делит таблицу распределения на две части таким образом, что вероятность попадания в одну из них равна 0,5. Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонения СВ от ее математического ожидания: Для дискретной случайной величины, которая принимает возможные значения xi с вероятностями pi (i=1,2,…,n) дисперсия рассчитывается по формуле: 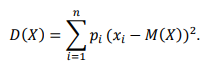 Для непрерывной случайной величины X вероятность 𝑃(𝑋 = 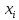 ) → 0, поэтому для нее удобнее использовать вероятность того, что случайная величина Х ) → 0, поэтому для нее удобнее использовать вероятность того, что случайная величина Хназывется интегральной функцией распределения. Интегральная функция является универсальным способом задания случайной величины (как для дискретной, так и для непрерывной). Дифференциальной функцией, функцией плотности вероятности непрерывной случайной величины X называется производная ее функции распределения: С помощью дифференциальной функции можно получить формулу вероятности попадания случайной величины X в заданный интервал: 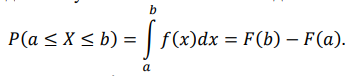 Математической ожидание непрерывной случайной величины Х определяется по формуле: 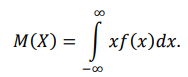 Если НСВ X определена на интервале (а; b), то: 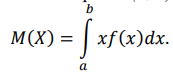 Мода НСВ X будет определяться как максимум ее дифференциальной функции: Медиана определяется как значение случайной величины, которое делит площадь под дифференциальной функцией на две равные части:  Дисперсия НСВ: Дисперсия случайной величины характеризует средний квадрат отклонения, поэтому на практике часто используют в качестве характеристики разброса среднее квадратическое отклонение: 6.3 Средства среды MatLab для статистической обработки данных К элементарной статистической обработке данных в массиве обычно относят нахождение их среднего значения, медианы и стандартного отклонения. Для этого определены следующие функции: - mean(A) возвращает арифметическое среднее значение элементов массива, если А – вектор; или возвращает вектор-строку, содержащую средние значения элементов каждого столбца, если А – матрица. Арифметическое среднее значение есть сумма элементов массива, деленная на их число; - mean(A,dim) возвращает среднее значение элементов по столбцам или по строкам матрицы в зависимости от значения скаляра dim (dim = 1 по столбцам и dim = 2 по строкам соответственно); - median(A) возвращает медиану, если А – вектор или вектор-строку медиан для каждого столбца, если А – матрица. Стандартное отклонение вычисляется следующей функцией: -std(X) возвращает стандартное отклонение элементов массиваX. 6.4 Порядок выполнения лабораторной работы  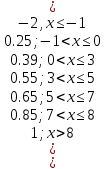 В лабораторной работе студент должен выполнить следующие задания: 6.4.1. Дискретная случайная величина Х задана рядом распределения (по варианту – таблица 6.1). Требуется найти по теоретическим формулам (используя среду MathCAD): - функцию распределения F(x); 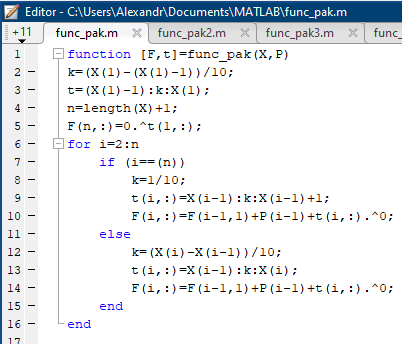 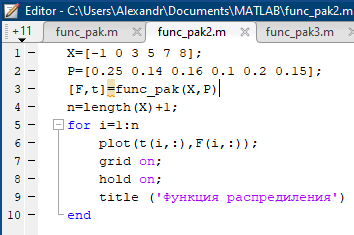 - построить график F(x); 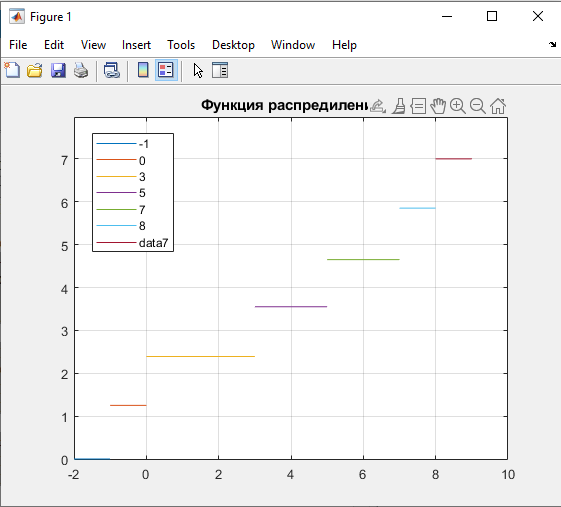 - числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение, моду;    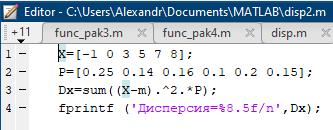 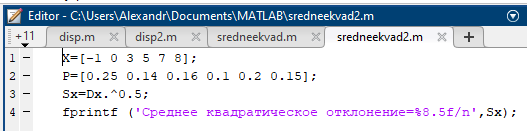 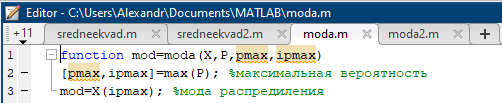 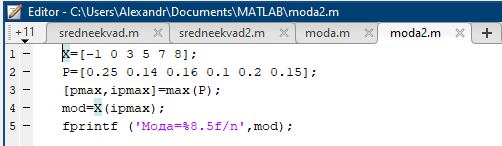 - вероятность попадания Х в интервал (a;b). 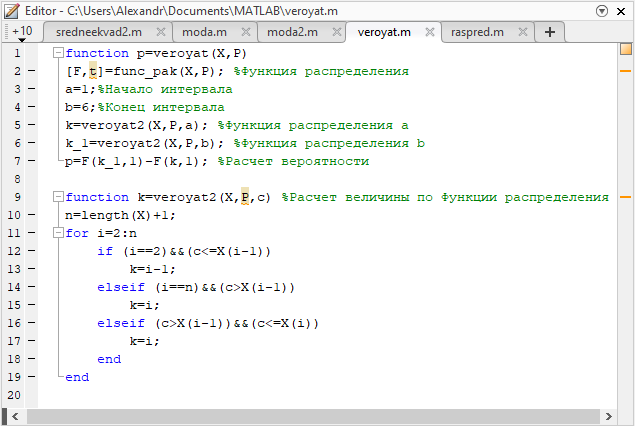 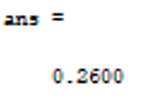 Построить графики F(x) и f(x). 6.4.2 Выполнить задание п.6.4.1, используя возможности системы MatLab. Сравнить результаты п.6.4.1 и 6.4.2. 6.4.3 Непрерывная случайная величина Х задана функцией распределения F(x) (по варианту – таблица 6.2). а) - плотность распределения f(x); a=0; b=2  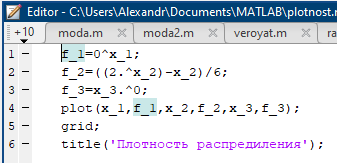 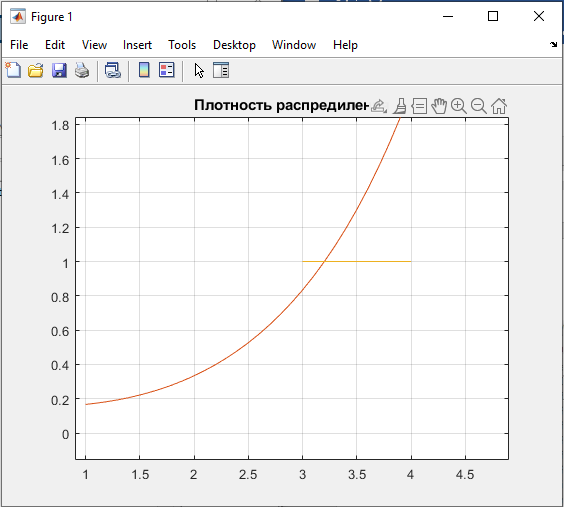 б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану; - математическое ожидание 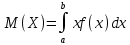 M(X)= 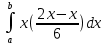 = =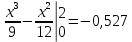 - дисперсия D(X)= 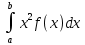 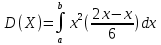 = =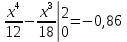 - среднее квадратическое отклонение 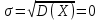 ,00 ,00- мода Mo(X)=maxf(x)=2 - медиана 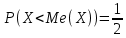 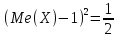  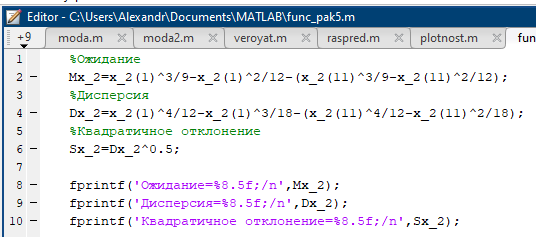 - функцию распределения F(x);  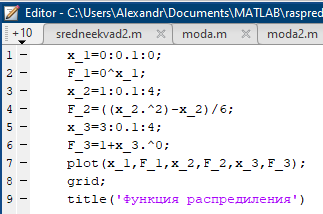 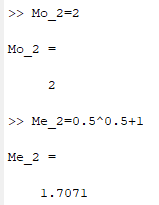 в) вероятность попадания Х в интервал (a;b). 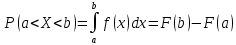 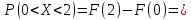 0,3333 0,3333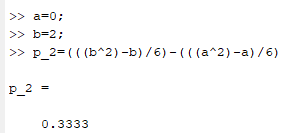 6.4.4 Выполнить задания п.6.4.3, используя возможности системы MatLab. Сравнить результаты п.6.4.3 и 6.4.4. 6.4.5 Непрерывная случайная величина Х задана плотностью распределения f(x) (по варианту – таблица 6.3). - функцию распределения F(x); f(x)= 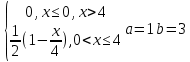 Преобразуем F(x)= 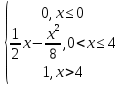 - математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану; -математическое ожидание 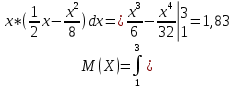 -дисперсия 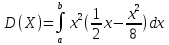 = =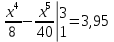 -среднее квадратическое отклонение 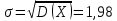 - мода 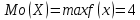 6.4.7. Случайная ошибка измерения подчинена нормальному закону распределения с параметрами а и (по варианту – таблица 6.4).  Требуется найти: - плотность распределения f(x); 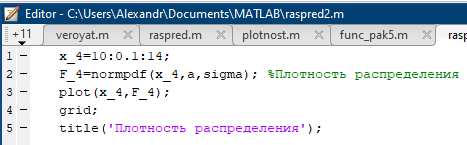 - вероятность попадания в интервал (, );  - вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине ;  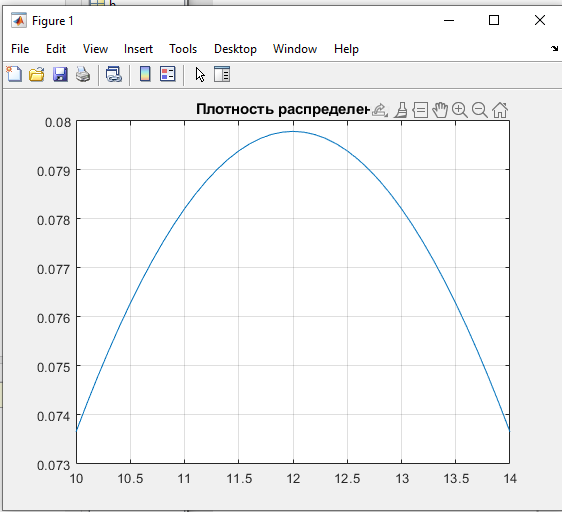 - функцию распределения F(x); 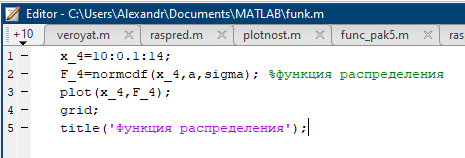 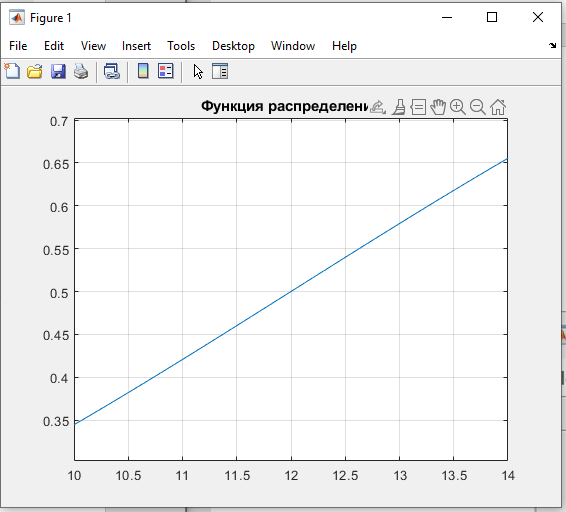 - вероятность попадания в интервал (, ); 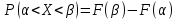 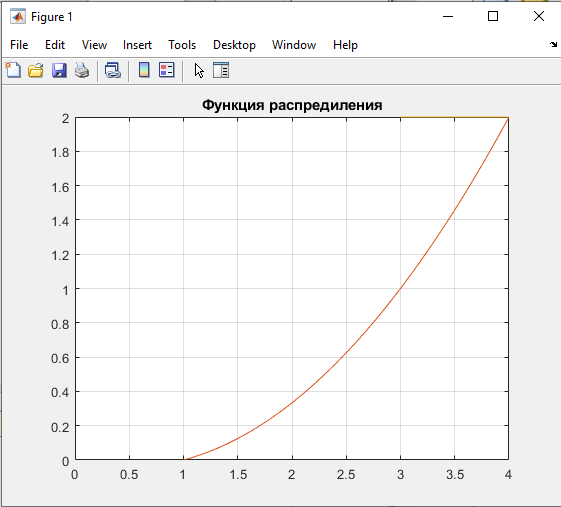 |
