Строительная механика. РГЗ№1 Селихов А.А. (1). Расчет многопролетных неразрезных балок методом теоремы трех моментов

• Название: Расчет многопролетных неразрезных балок методом теоремы трех моментов
• Анкор: Строительная механика
• Дата: 04.04.2021
• Размер: 392.91 Kb.
• Имя файла: РГЗ№1 Селихов А.А. (1).docx
• Тип: Документы; #191244

Министерство науки И ВЫСШЕГО ОБРАЗОВАНИЯ

Российской Федерации



Федеральное государственное бюджетное образовательное учреждение высшего образования

Санкт-Петербургский горный университет

ВАРИАНТ В765
По дисциплине СТРОИТЕЛЬНАЯ МЕХАНИКА

(наименование учебной дисциплины, согласно учебному плану)

Тема: Расчет многопролетных неразрезных балок методом теоремы трех моментов

Выполнил: студент гр. ГС-18-2 Чернова К.О.

(подпись) (Ф.И.О.)



Проверил: профессор Трушко В.Л.

(подпись) (Ф.И.О.)

Санкт-Петербург

2021 год

Исходные данные:

P, кН	q, кН/м	l, м	а, м	n/k
4	16	6,2	2,0	1,8/2

Схема балки: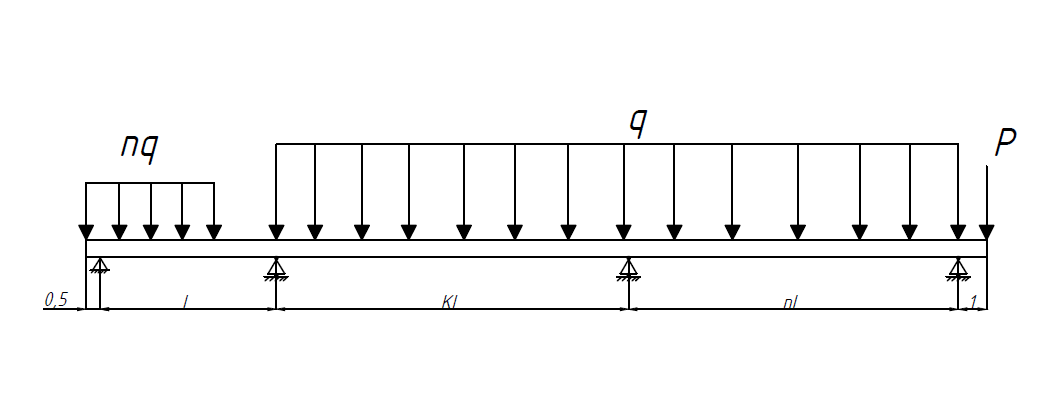



Для раскрытия статической неопределимости балки по теореме трех моментов используем следующие методы:

1. 
   Мысленно разрежем балку на каждой опоре и введем шарниры
   
2. 
   Компенсируем введение шарниров реактивными опорными моментами
   
3. 
   Составим уравнения совместности деформации из условия, что углы поворота сечений балки слева и справа на каждой опоре равны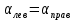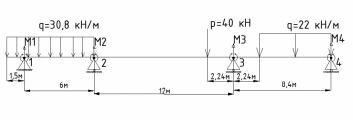
   

Составим уравнения совместности деформации:

1. 
   Для 1 опоры: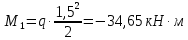
   

2. 
   Для 2 опоры: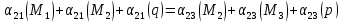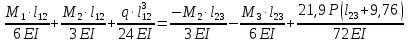
   

3. 
   Для 3 опоры: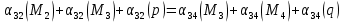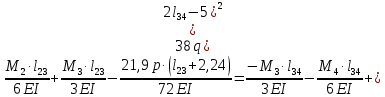
   

4. 
   Для 4 опоры: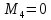
   

Получили систему из 4 уравнений. Решая данную систему, найдем неизвестные реактивные опорные моменты.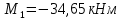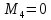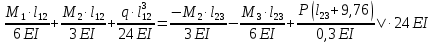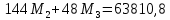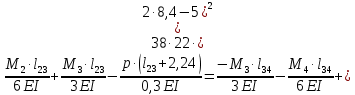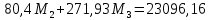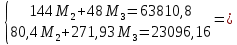















Тогда реактивные опорные моменты на каждой опоре равны: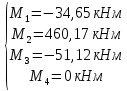



Далее составим уравнения реакции: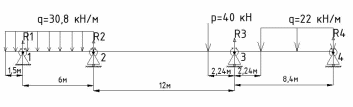

1. 
   Для 1 опоры: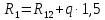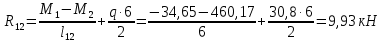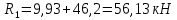
   

2. 
   Для 2 опоры: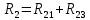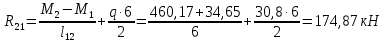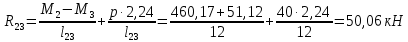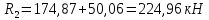
   

3. 
   Для 3 опоры: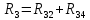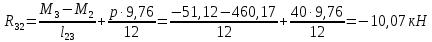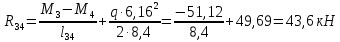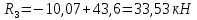
   

4. 
   Для 4 опоры: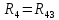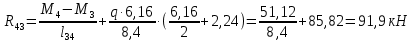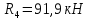
   

Проверим правильность найденных реакций путем проецирования всех действующих сил на вертикальную ось

∑y = 0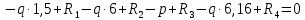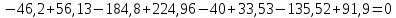





В результате опорные реакции принимают следующие значения: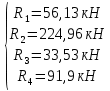



Эпюры изгибающих моментов и перерезывающих сил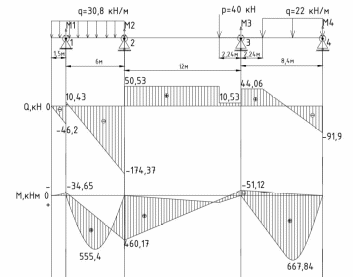



Из эпюры изгибающих моментов видно, что максимальный момент равен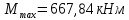



Момент сопротивления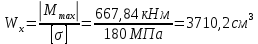



где 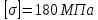нормативное напряжение для стали

По сортаменту прокатной стали ГОСТ 26020-83 подбираем двутавровую балку 70Б2 ( )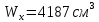

Случай 2. Две средние опоры балки являются податливыми, две боковые жесткими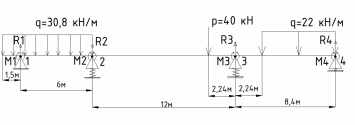



Составим уравнения совместности деформации:

1. 
   Для 1 опоры: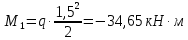
   

2. 
   Для 2 опоры: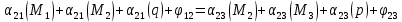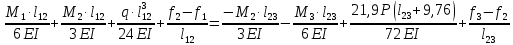
   

3. 
   Для 3 опоры: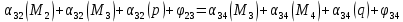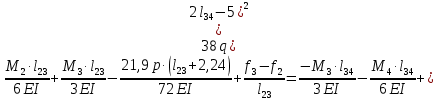
   

4. 
   Для 4 опоры: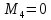
   

Т.к. 1-ая и 4-ая опоры жесткие, то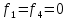

Составим дополнительные уравнения для проседания опор

1. 
   Для 2 опоры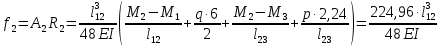
   

2. 
   Для 3 опоры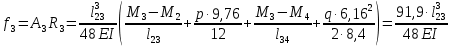
   

где 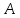– коэффициент податливости опор

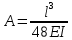Подставим получившиеся уравнения проседания в основную систему уравнений и найдем неизвестные реактивные опорные моменты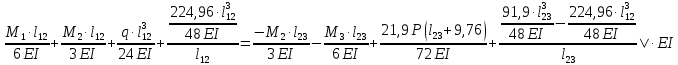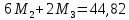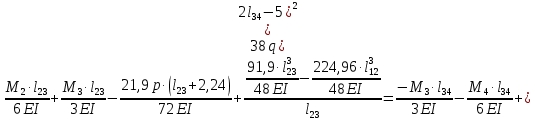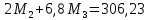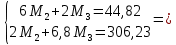











Тогда реактивные опорные моменты на каждой опоре равны: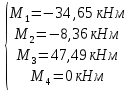



Далее составим уравнения реакции:

1) Для 1 опоры: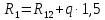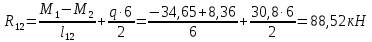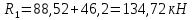

2. 
   Для 2 опоры: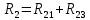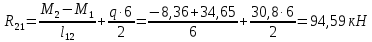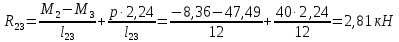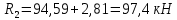
   

2. 
   Для 3 опоры: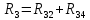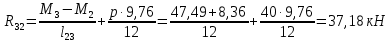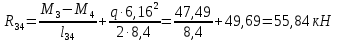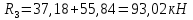
   

2. 
   Для 4 опоры: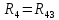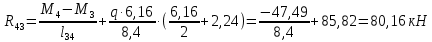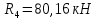
   

Проверим правильность найденных реакций путем проецирования всех действующих сил на вертикальную ось

∑y = 0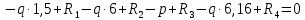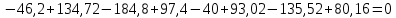





В результате опорные реакции принимают следующие значения: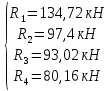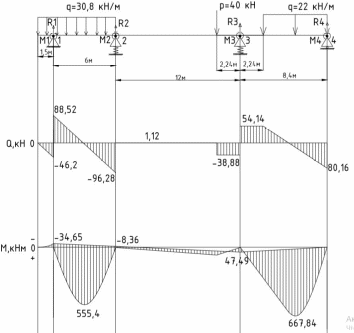





Из эпюры изгибающих моментов видно, что максимальный момент равен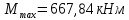

Момент сопротивления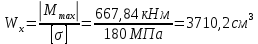



где 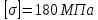нормативное напряжение для стали

По сортаменту прокатной стали ГОСТ 26020-83 подбираем двутавровую балку 70Б2 ( 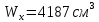)