Расчёт на прочность и жёсткость навеса. Пример. Расчёт на прочность и жёсткость элементов навеса
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
3.2 Расчет прогона3.2.1 Расчет прогона на прочностьДля расчёта на прочность мы должны определиться с грузовой площадью прогона и нагрузками действующими на него. Грузовая площадь – это площадь, с которой нагрузка передается на элемент конструкции, она будет равна половине пролета. Вид сверху навеса показан на рисунке 18.     2 1 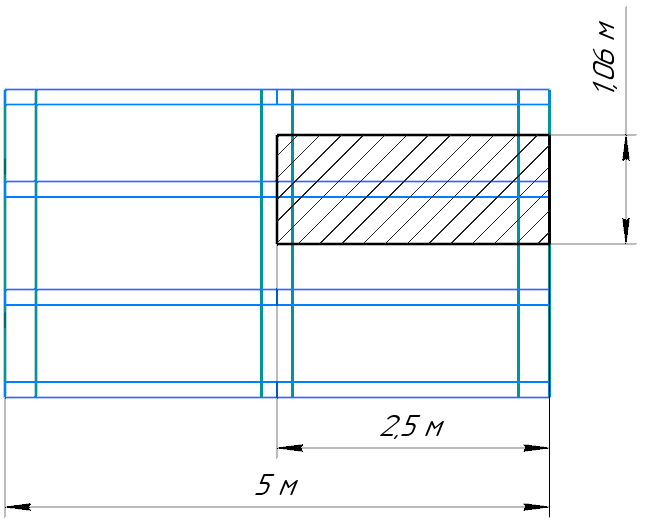 Рисунок 18 – Вид сверху навеса: 1 – прогон; 2 – грузовая площадь прогона Выбран этот прогон так как у него самая большая грузовая площадь и соответственно на него действует наибольшая нагрузка. Определим все нагрузки действующие на прогон. Вначале определим линейную снеговую нагрузку по формуле: 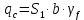 , (5) , (5)где 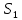 – значение снеговой нагрузки, – значение снеговой нагрузки, 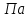 ; ;b – ширина грузовой площади, м; 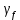 – нормативный коэффициент безопасности по нагрузке, б/р; – нормативный коэффициент безопасности по нагрузке, б/р;Нормативный коэффициент безопасности по нагрузке – это коэффициент, учитывающий в условиях нормальной эксплуатации сооружений возможное отклонение нагрузок в неблагоприятную сторону от нормативных значений, для снеговой и ветровой нагрузки принимают значение 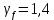 , для профилированного листа и металлических конструкций , для профилированного листа и металлических конструкций 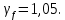 Данные коэффициенты взяты из СП 20.13330.2016. Данные коэффициенты взяты из СП 20.13330.2016.Подставляем все значения и получаем: 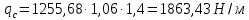 . . Остальные нагрузки будут определяться аналогично. Ветровая нагрузка составит: 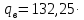 1,06 1,06 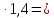 196,26 Н/м. 196,26 Н/м.Нагрузка от профилированного листа составит: 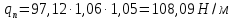 . .Теперь высчитаем нагрузку от собственного веса прогона, как линейно распределенную нагрузку по формуле: 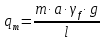 , (6) , (6)где 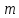 – масса 1 метра швеллера, кг/м; – масса 1 метра швеллера, кг/м;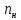 – нормативный коэффициент безопасности по нагрузке, б/р; – нормативный коэффициент безопасности по нагрузке, б/р;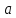 – длина прогона, м; – длина прогона, м;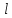 – длина, на которую действует линейно распределенная нагрузки, м; – длина, на которую действует линейно распределенная нагрузки, м;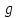 – ускорение свободного падения. – ускорение свободного падения.Массу 1 метра сечения возьмём из таблицы 2, для швеллера №6.5 m = 5,9 кг, длина прогона 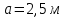 , длина, на которую действует линейно распределенная нагрузки, в данном случае, равна длине прогона , длина, на которую действует линейно распределенная нагрузки, в данном случае, равна длине прогона 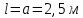 . Подставляем значения: . Подставляем значения: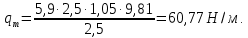 Теперь сложим все значения нагрузок и получим суммарную нагрузку действующую на прогон: 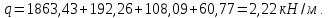 Далее для построения эпюр составим 2 уравнения равновесия: 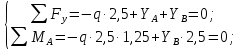 (7) (7)Решая данную систему уравнений находим реакции опор: 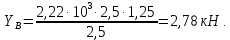 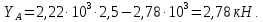 Теперь изобразим расчетную схему и построим эпюры поперечных сил и изгибающих моментов для прогона (рисунок 19). 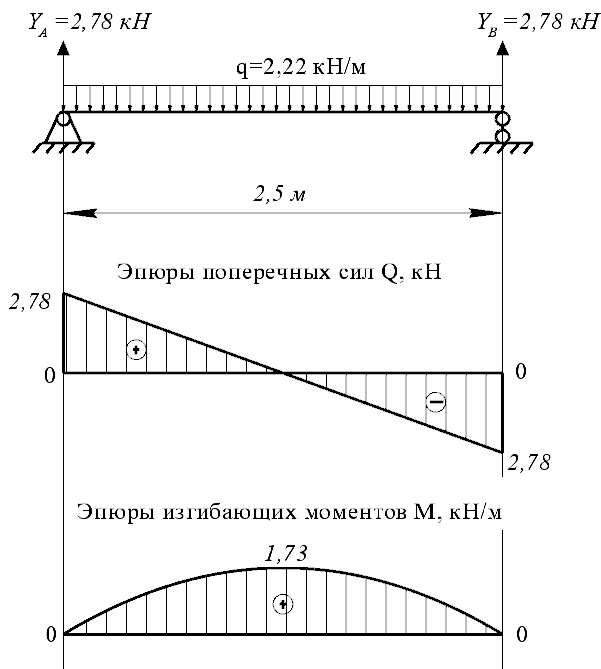 Рисунок 19 – Эпюры поперечных сил и изгибающих моментов прогона Высчитаем допускаемое напряжение по формуле: 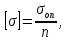 (8) (8)где 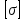 ‒ допускаемое напряжение, Па; ‒ допускаемое напряжение, Па;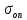 – опасное напряжение, Па; – опасное напряжение, Па;n – коэффициент запаса прочности, б/р. Опасным напряжением для нашей стали будет предел текучести, который возьмём из таблицы 1, 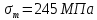 . Коэффициент запаса прочности примем равным . Коэффициент запаса прочности примем равным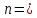 1.6 в соответствие с СП 20.13330.2016. Тогда допускаемое напряжение будет: 1.6 в соответствие с СП 20.13330.2016. Тогда допускаемое напряжение будет: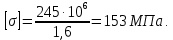 Условие прочности имеет вид: 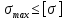 (9) (9)где 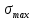 ‒ максимальное напряжение, Па; ‒ максимальное напряжение, Па;Максимальное напряжение, создаваемое поперечными силами или изгибающими моментами можно найти по следующей формуле: 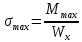 , (10) , (10)где 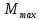 ‒ максимальное значение изгибающего момента, Нм; ‒ максимальное значение изгибающего момента, Нм;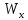 ‒ осевой момент сопротивления сечения, ‒ осевой момент сопротивления сечения, 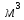 ; ;Осевой момент сопротивления возьмём из таблицы 2 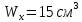 . Максимальное значение изгибающего момента найдём по формуле: . Максимальное значение изгибающего момента найдём по формуле: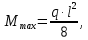 (11) (11)где 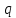 ‒ распределенная нагрузка действующая на прогон, Н/м; ‒ распределенная нагрузка действующая на прогон, Н/м; 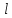 ‒ длина прогона, м. ‒ длина прогона, м. Получаем значение максимального изгибающего момента: 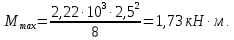 Найдем значение максимального напряжения и сравним его с допускаемым: 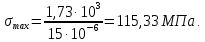 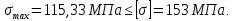 Условие прочности выполняется. 3.2.2 Расчет прогона на жесткостьПомимо прочности прогон должен обладать жесткостью, то есть деформироваться под заданной нагрузкой в допустимых пределах. Так как прогон является балкой, то для оценки жесткости используют максимальное перемещение 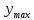 и оно не должно превышать допускаемое перемещение, которое для балок длиной от 1 м до 3 м включительно рассчитывается по формуле [8]: и оно не должно превышать допускаемое перемещение, которое для балок длиной от 1 м до 3 м включительно рассчитывается по формуле [8]: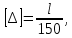 (12) (12)где l‒ длина прогона, м. Подставив длину, получаем: 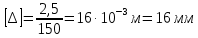 Условие жёсткости имеет вид: 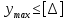 (13) (13)где 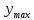 ‒ максимальный прогиб, м. ‒ максимальный прогиб, м.Для определения прогиба балки, лежащей концами на двух опорах и нагруженной по всей длине равномерно воспользуемся формулой [10] c. 28: 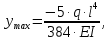 (14) (14)где q‒приложенная сила, Н/м; l‒ длина балки, м; E‒ модуль Юнга, Па; 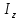 ‒ осевой момент инерции сечения, ‒ осевой момент инерции сечения, 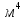 ; ;Найдём прогиб прогона: 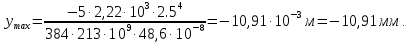 Проверим выполнение условия жёсткости: 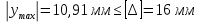 . .Условие жесткости выполняется. |
