Расчёт на прочность и жёсткость навеса. Пример. Расчёт на прочность и жёсткость элементов навеса
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
3.3 Расчет балки3.3.1 Расчет балки на прочностьВначале, как и в расчете прогона, мы должны определиться с грузовой площадью и нагрузками (рисунок 20). Будем рассчитывать балку, которая находится посередине, так как у неё будет самая большая грузовая площадь.     2 1 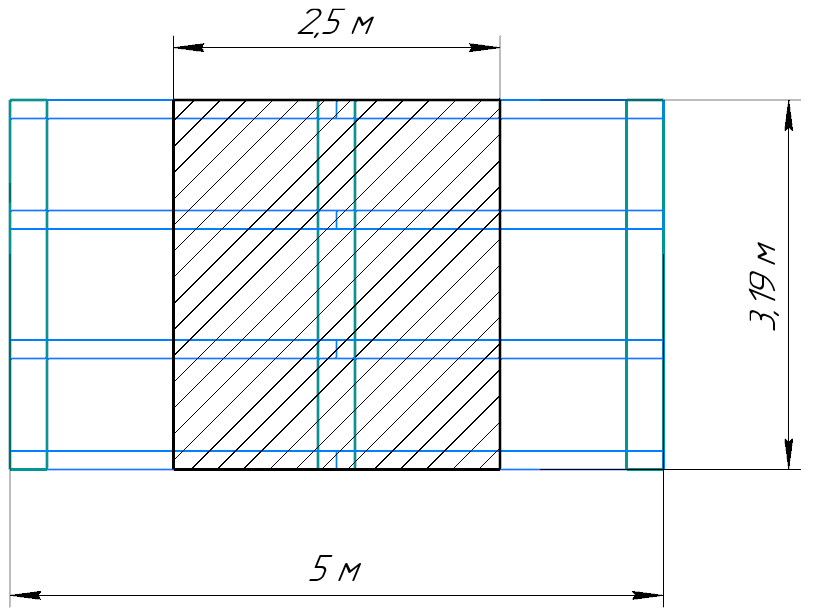 Рисунок 20 – Вид сверху навеса: 1 ‒ балка; 2 ‒ грузовая площадь балки На балку будут действовать те же нагрузки, что и на прогон, но дополнительно будет действовать вес от прогонов попадающих в грузовую площадь. Для расчёта нагрузки от прогонов воспользуемся формулой 6, взяв 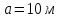 , так как в заштрихованную область на рисунке 20 попадает половина восьми прогонов, длина на которую действует распределенная нагрузка будет равна длине балки , так как в заштрихованную область на рисунке 20 попадает половина восьми прогонов, длина на которую действует распределенная нагрузка будет равна длине балки 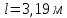 : :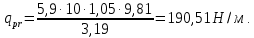 Теперь найдём снеговую нагрузку по формуле 5: 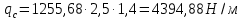 . . Ветровая составит: 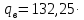 2,5 2,5 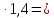 462,88 Н/м. 462,88 Н/м.Нагрузка от профлиста будет равна: 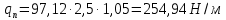 . .Нагрузку от собственного веса будем находить по аналогии по формуле 6, приняв массу 1 метра двутавра из таблицы 2: 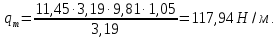 Теперь высчитаем суммарную нагрузку: 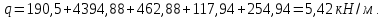 С помощью данной нагрузки найдём силы действующие на балку по формулам: 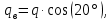 (15) (15)где 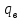 ‒ вертикальная проекция суммарной нагрузки, Н/м; ‒ вертикальная проекция суммарной нагрузки, Н/м;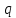 ‒ суммарная нагрузка, Н/м. ‒ суммарная нагрузка, Н/м.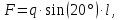 (16) (16)где 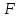 ‒ горизонтальная проекция суммарной нагрузки, Н/м; ‒ горизонтальная проекция суммарной нагрузки, Н/м;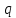 ‒ суммарная нагрузка, Н/м; ‒ суммарная нагрузка, Н/м;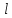 ‒ длина балки, м. ‒ длина балки, м.Найдём численные значения данных нагрузок: 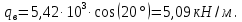 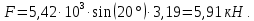 Далее для построения эпюр составим 3 уравнения равновесия: 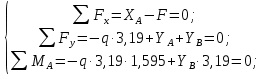 (17) (17)Решая данную систему уравнений находим реакции опор: 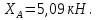 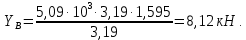 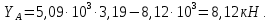 Изобразим расчетную схему и построим эпюры продольных, поперечных сил и изгибающих моментов (рисунок 21): 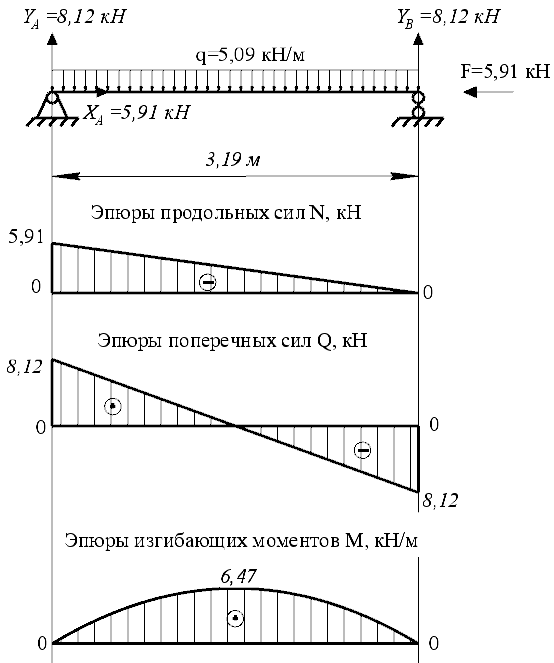 Рисунок 21 – Эпюры продольных, поперечных сил и изгибающих моментов балки Определим максимальный изгибающий момент для балки по формуле 11: 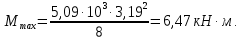 Определим максимальное напряжение по формуле [10] c. 305: 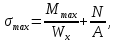 (18) (18)где 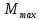 ‒максимальный изгибающий момент, Нм; ‒максимальный изгибающий момент, Нм;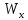 ‒ осевой момент сопротивления, ‒ осевой момент сопротивления, 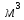 ; ;N‒ максимальная продольная сил, Н; A ‒площадь поперечного сечения, 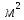 . .Осевой момент сопротивления и площадь поперечного сечения возьмём из таблицы 2. Для двутавра 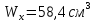 , A=14,7 , A=14,7 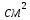 . Значения изгибающего момента и продольной силы берём из эпюр. Подставляем значения в формулу и находим максимальное напряжение: . Значения изгибающего момента и продольной силы берём из эпюр. Подставляем значения в формулу и находим максимальное напряжение: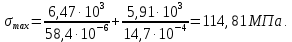 Сравним его с допускаемым напряжением, полученным по формуле 8: 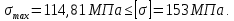 Условие прочности не выполняется. 3.3.2 Расчет балки на жесткостьТак же, как и для прогона, балка должна обладать жесткостью. Для определения допускаемого прогиба воспользуемся формулой 14: 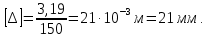 Для определения прогиба балки, лежащей концами на двух опорах и нагруженной по всей длине равномерно воспользуемся формулой: 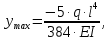 (19) (19)где q‒приложенная сила, Н/м; l‒ длина балки, м; E‒ модуль Юнга, Па; 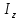 ‒ осевой момент инерции сечения, ‒ осевой момент инерции сечения, 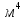 ; ;Взяв из таблицы 2 осевой момент инерции сечения 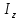 =350 c =350 c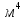 находим максимальный прогиб: находим максимальный прогиб: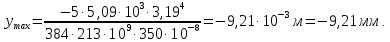 Проверим выполнение условия жёсткости: 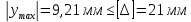 . .Условие жесткости выполняется. |
