КУРСАЧ СОСЕДА. Расчёт основных характеристик цифровой системы связи с использованием квадратурной модуляции
 Скачать 2.37 Mb. Скачать 2.37 Mb.
|
|
3.3. Кодер Требуется: 1. Использовать свёрточный код с параметрами: - степень кодирования k/n = 1/2, - длина кодового ограничения K = 3, - векторы связи 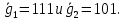 2. Нарисовать схему кодера, соответствующую заданным параметрам, и определить его импульсную характеристику g(x). Рисунок свёрточного кодера, соответствующего заданным параметрам показан на рисунке 3.3.1. 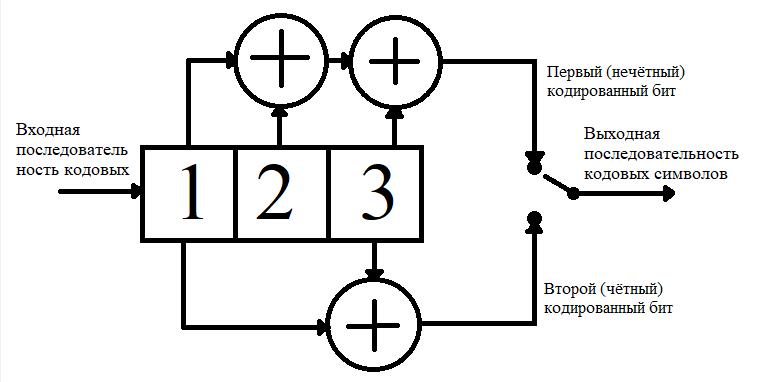 Рисунок 3.3.1. Структурная схема кодера 3. Изобразить решетчатую диаграмму свёрточного кодера от момента времени t1 до момента времени t10. (рис. 3.3.2) 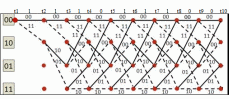 Рисунок 3.3.2. Решетчатая диаграмма свёрточного кода 4. На решетчатой диаграмме свёрточного кодера построить путь, соответствующий последовательности информационных символов 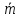 от АЦП для заданного уровня квантованияj, и определить по нему последовательность кодовых символов от АЦП для заданного уровня квантованияj, и определить по нему последовательность кодовых символов 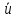 на выходе кодера. на выходе кодера.Решетчатая диаграмма свёрточного кодера от момента времени t1 до момента времени t10 с отмеченным путем, соответствующим полученными кодовыми символами 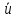 =111011100, показана на рисунке 3.3.3. =111011100, показана на рисунке 3.3.3. 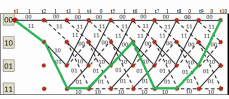 Рисунок 3.3.3. Решетчатая диаграмма свёрточного кодера от момента времени t1 до момента времени t10 На выходе кодера получена последовательность КС 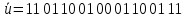 соответствующие заданному уровню квантования j. соответствующие заданному уровню квантования j.5. Определить длительность двоичного символа ТВ на выходе кодера (в последовательном формате) 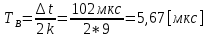 6. Определить техническую скорость передачи VВ 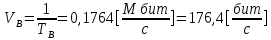 3.4. Формирователь модулирующих сигналов Формирователь модулирующих сигналов (ФМС) предназначен для преобразования двоичного цифрового потока от кодера C(t) в модулирующие сигналы I(t) иQ(t), которые необходимо подавать на синфазный и квадратурный входы модулятора для получения заданного сигнального созвездия на его выходе. Он должен содержать: - регистр сдвига для деления входного потока бит от кодера на группы, передаваемые одним сигналом sКАМ(t) дибиты при QPSK - преобразователи уровней битовых сигналов (униполярной кодировки в биполярную: при QPSK «0» → h, «1» → –h; Требуется: 1. Изобразить сигнальное созвездие для заданного вида модуляции. Сигнальное созвездие для КФМ-4 продемонстрировано на рисунке 3.4.1. 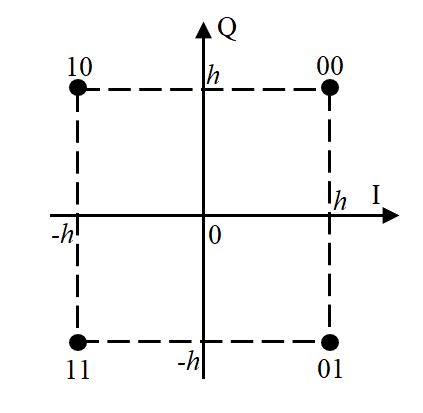 Рисунок 3.4.1. Сигнальное созвездие Квадратурной Фазовой Модуляции(КФМ-4). 2. Изобразить график реализации c(t) случайного процесса C(t) на входе блока ФМС (выходе свёрточного кодера) для первых 16 бинарных интервалов (рис. 3.4.2).  Рисунок 3.4.2. Осциллограмма реализации c(t) на выходе свёрточного кодера. Написать аналитическое выражение для случайного процесса 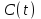 . .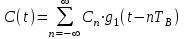 где 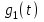 прямоугольный импульс длительностью прямоугольный импульс длительностью 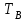 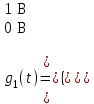 при при 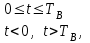 где 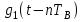 прямоугольный импульс такой же формы, как прямоугольный импульс такой же формы, как 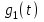 , но сдвинутый вправо относительно импульса , но сдвинутый вправо относительно импульса 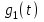 на величину на величину 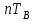 , если , если 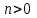 , или влево, если , или влево, если 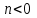 ; ; 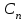 - случайная величина 0, +h(значение бита на - случайная величина 0, +h(значение бита на 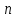 - интервале - интервале 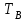 ). ).3. В соответствии с сигнальным созвездием модулятора КФМ-4. Изобразить для входной реализации 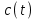 графики реализаций графики реализаций 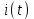 и и 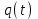 на выходе блока ФМС случайных процессов на выходе блока ФМС случайных процессов 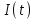 и и 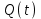 (рис. 3.4.3). Написать аналитические выражения для случайных процессов (рис. 3.4.3). Написать аналитические выражения для случайных процессов 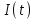 и и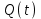 . .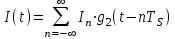 ; ; 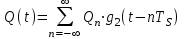 где 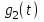 прямоугольный импульс длительностью TS= 2∙TB = 2 ∙ 5,67[мкс] = 11,33 [мкс] прямоугольный импульс длительностью TS= 2∙TB = 2 ∙ 5,67[мкс] = 11,33 [мкс] 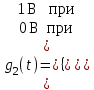 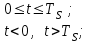 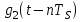 прямоугольный импульс такой же формы, как импульс прямоугольный импульс такой же формы, как импульс 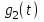 , но сдвинутый вправо относительно импульса , но сдвинутый вправо относительно импульса 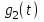 на величину на величину 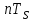 , если , если 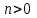 , или влево, если , или влево, если 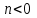 ; ; 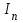 и и 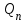 независимые случайные величины, заданные на символьном интервале с номером независимые случайные величины, заданные на символьном интервале с номером 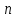 , которые согласно сигнальному созвездию (рис. 3.4.1) принимают: , которые согласно сигнальному созвездию (рис. 3.4.1) принимают:Для КФМ-4 два дискретных значения –h, +h с вероятностью 0,5 каждое, т. е. 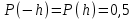 ; ;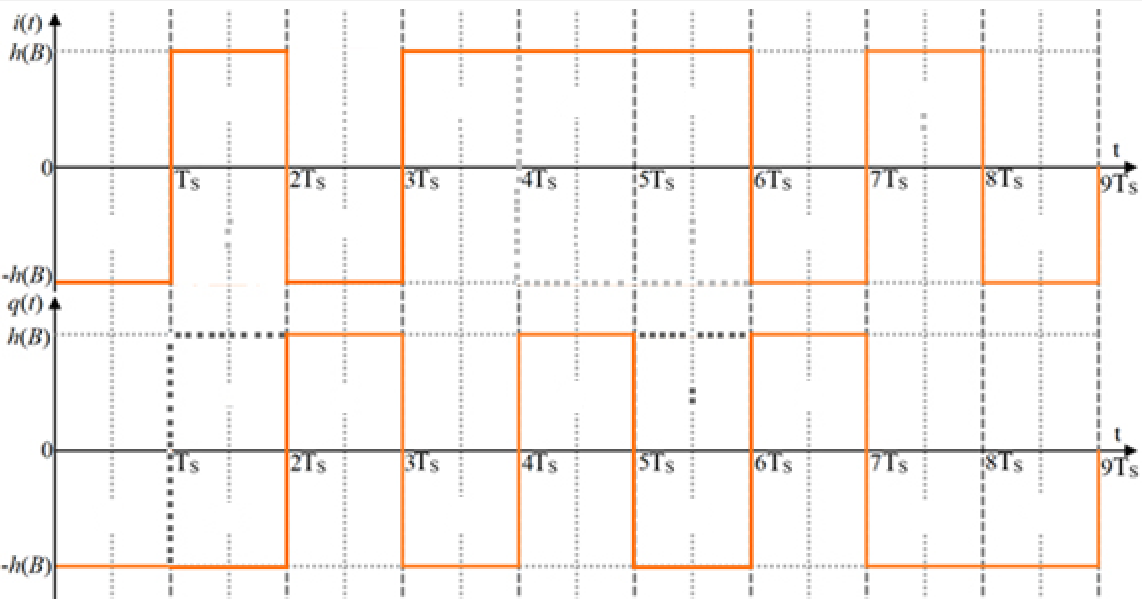 Рисунок 3.4.3 Графики реализаций входной c(t) для случайных процессов I(t) и Q(t) на выходе блока ФМС. Написать аналитические выражения для корреляционной функции 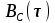 и спектральной плотности мощности и спектральной плотности мощности 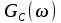 входного случайного процесса входного случайного процесса 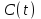 и построить графики этих функций. и построить графики этих функций.Процесс C(t) является случайным синхронным телеграфным сигналом. Его корреляционная функция имеет вид [1], а его график изображен на рисунке 3.4.4.1. 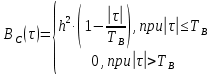 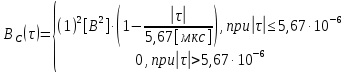 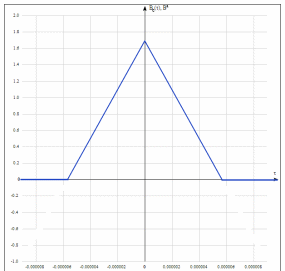 Рисунок 3.4.4.1. График корреляционной функции BC(τ) случайного процесса C(t) а энергетический спектр задается Gc(f) – график изображен на рисунке 3.4.4.2. 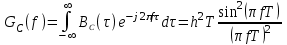 , ,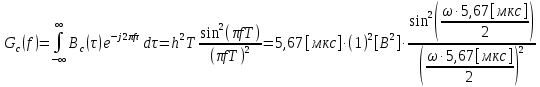 где Т = ТВ – длительность тактового интервала. ω = fT 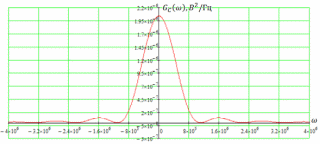 Рисунок 3.4.4.2. График спектральной плотности мощности GC(ω) случайного процесса C(t) 5. Написать аналитические выражения для корреляционных функций BI(τ) и BQ(τ), спектральных плотностей мощности GI(f) и GQ(f) случайных процессов I(t) и Q(t). Построить графики этих функций. Процессы I(t) и Q(t) отличаются от процесса C(t) длительностями тактовых интервалов (TS = 2TB). 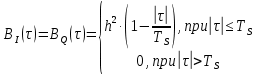 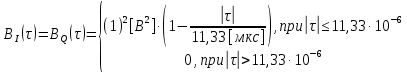 График корреляционной функции случайных процессов I(t) и Q(t) на выходе ФМС изображен на рисунке 3.4.5.1.  1,69 - 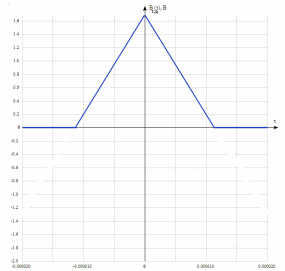 Рисунок 3.4.5.1. График корреляционной функции случайных процессов I(t) и Q(t) Спектральные мощности GI(ω) и GQ(ω) на выходе ФМС (рис. 3.4.5.2.): 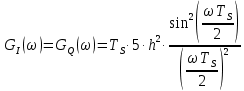 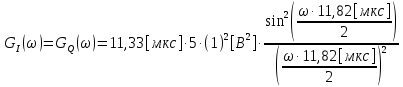    | 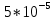 | 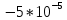 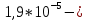 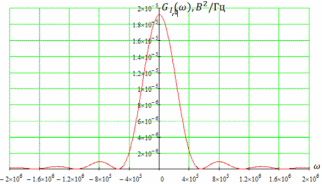 Рисунок 3.4.5.2.График спектральной плотности мощности случайных процессов I(t) и Q(t) 6. Сравнить графики корреляционных функций и спектральных плотностей мощности сигналов на входе и выходе блока ФМС. Привести краткое описание результатов сравнения и, используя общие положения теории преобразования Фурье, пояснить, почему спектр выходных сигналов уже спектра входного сигнала. Отличие BI(τ) и BQ(τ) от корреляционной функции BС(τ) проявляется в том, что вместо параметра TB используется параметр TS, где TS – символьный интервал, который в два раза больше первого. (рис. 3.4.6.1). Форма графика функций GQ(ω) и GI(ω) будет похожа на форму графика GC(ω) на рис.3.4.6.2. Величина главного максимума станет больше и будет равна TS∙h2 и в точках 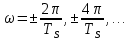 график этих функций будет касаться оси абсцисс ω. график этих функций будет касаться оси абсцисс ω.    | 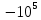 | 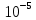 1,69 - 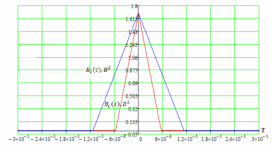 Рисунок 3.4.6.1. Сравнение графиков корреляционных функций сигналов на входе и выходе блока 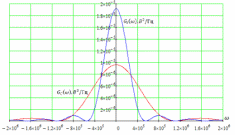 Рисунок 3.4.6.2. Сравнение графиков спектральных плотностей мощности сигналов на входе и выходе блока ФМС Для КФМ-4 согласно свойствам преобразований Фурье, спектр выходных сигналов уже, так как длительность параллельных импульсов в два раза выше, чем последовательного кода, TS = 2∙TB. 3.5. Модулятор Структурная схема модулятора в соответствии с [1] представлена на рисунке 3.5.1.1. В состав модулятора структурной схемы цифровой системы связи (ЦСС), рис. 1, между блоками ФМС и перемножителями входят сглаживающие формирующие фильтры СФФ, необходимые для оптимизации ЦСС в отношении межсимвольной помехи, а также инвертор и сумматор, на выходе которого получаем сигнал заданного вида модуляции. 3.5.1. Сглаживающий формирующий фильтр 1. Изобразить структурную схему модулятора в составе ЦСС; 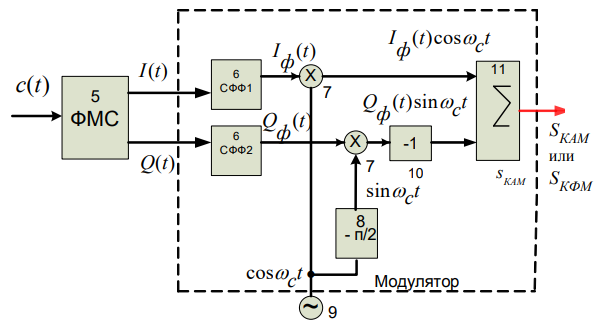 Рис. 3.5.1.1. Структурная схема модулятора в составе ЦСС 2. Написать аналитические выражения для сигнала x(t) со «спектром приподнятого косинуса» (импульса Найквиста) и его спектральной плотности Sx(f) для значений коэффициента сглаживания 01. Изобразить графики сигналов x(t) и соответствующие спектральные плотности при 0 1. 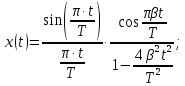 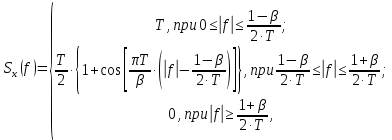 Графики импульсов Найквиста x(t) и их спектральных плотностей для значений коэффициента β = 0; 0,25; 0,5; 1 приведены на рисунках 3.5.1.2 и 3.5.1.3. 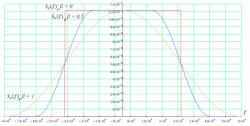 Рис. 3.5.1.2. Импульсы Найквиста x(t) 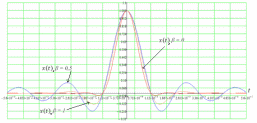 Рис. 3.5.1.3. Спектральные плотности Sx(f) импульсов Найквиста. 3. На одном рисунке изобразить графики спектральных плотностей Sx() и Sx1() сигналов x(t) и x1(t), где x(t) – импульс Найквиста при коэффициенте сглаживания β =1 ; x1(t) – импульс со спектральной плотностью 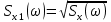 .(рис 3.5.1.4) .(рис 3.5.1.4)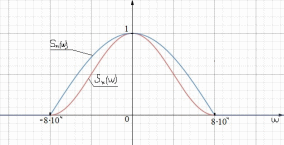 Рис. 3.5.1.4. Спектральные плотности Sx(ω) и Sx1(ω). 4. На одном рисунке изобразить графики импульсов x(t) и x1(t) С помощью обратного преобразования Фурье от функции Sx1(ω): 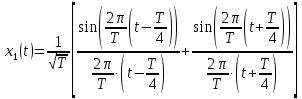 График импульсов x(t) и x1(t) продемонстрированы на рисунке3.5.1.5. 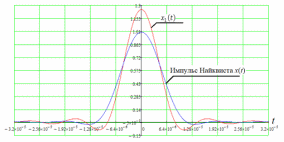 Рисунок 3.5.1.5. Импульс Найквиста x(t) и искомый импульс x1(t). 5. Написать аналитические выражения для случайных процессов Iф(t) и Qф(t); На вход СФФ поступает реализация 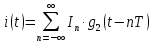 где 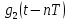 – прямоугольные импульсы. – прямоугольные импульсы.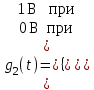  На выходе СФФ получается  где  имеют форму импульсов x1н(t); имеют форму импульсов x1н(t); 6. Написать аналитические выражения для корреляционных функций (рис.3.5.1.6) и спектральных плотностей мощности случайных процессов Iф(t) и Qф(t) (рис.3.5.1.7) и построить графики этих функций. 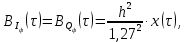 где x(τ) – импульс Найквиста при значении β = 1. 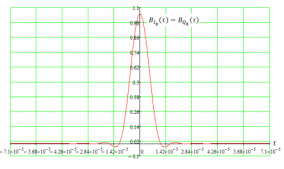 Рисунок 3.5.1.6. График корреляционных функций 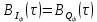 Аналитические выражения для спектральных плотностей мощности случайных процессов Iф(t) и Qф(t): 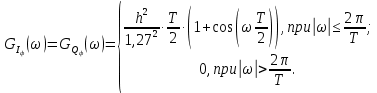 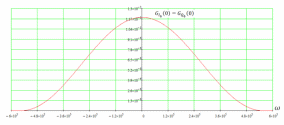 Рисунок 3.5.1.7. График спектральных плотностей мощности 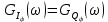 |
