КУРСАЧ СОСЕДА. Расчёт основных характеристик цифровой системы связи с использованием квадратурной модуляции
 Скачать 2.37 Mb. Скачать 2.37 Mb.
|
|
3.5.2. Блоки перемножителей, инвертор, сумматор 1. Написать аналитические выражения для корреляционных функций 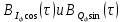 случайных сигналов случайных сигналов 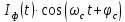 и и 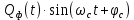 на выходах перемножителей, где с – случайная фаза с равномерной плотностью вероятности на интервале 0…2 . Случайная фаза с не зависит от случайных процессов на выходах перемножителей, где с – случайная фаза с равномерной плотностью вероятности на интервале 0…2 . Случайная фаза с не зависит от случайных процессов 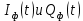 . .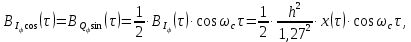 где 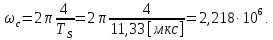 2. Корреляционная функция 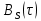 сигнала сигнала 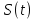 на выходе сумматора для КФМ-4(рис. 3.5.2.1): на выходе сумматора для КФМ-4(рис. 3.5.2.1):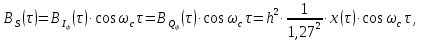 где x(τ) – импульс Найквиста при β = 1. 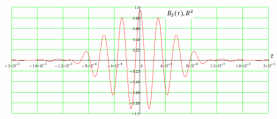 Рисунок 3.5.2.1. График корреляцонной функции Bs(τ) Спектральная плотность мощности 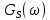 сигнала сигнала 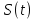 на выходе сумматора (рис. 3.5.2.2) для КФМ-4: на выходе сумматора (рис. 3.5.2.2) для КФМ-4: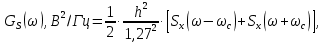 где где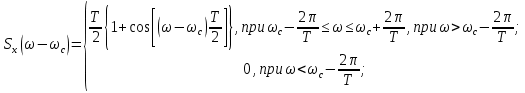 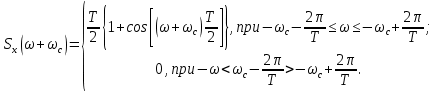 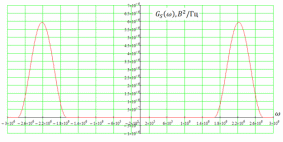 Рисунок 3.5.2.2. График спектральной плотности мощности 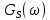 3.6. Непрерывный канал Передача сигнала S(t) происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии аддитивной помехи n(t) типа гауссовского белого шума. Сигнал Z(t) на выходе такого канала имеет вид 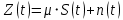 где 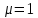 – коэффициент передачи канала. Односторонняя спектральная плотность мощности помехи n(t) равна N0 = 4 * 10-7 – коэффициент передачи канала. Односторонняя спектральная плотность мощности помехи n(t) равна N0 = 4 * 10-71. Определить минимальную ширину полосы частот Fk непрерывного канала, необходимую для передачи по каналу сигнала S(t) с выхода модулятора; 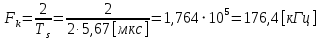 2. Определить Pс – среднюю мощность информационного сигнала 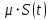 на выходе канала; на выходе канала; 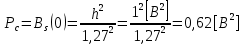 3. Определить Pп – среднюю мощность помехи n(t) на выходе канала и найти отношение Pс / Pп ; 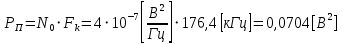 Отношение сигнал/помеха: 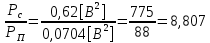 Защищенность сигнала в канале: 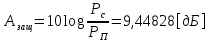 4. Рассчитать пропускную способность C (за секунду) непрерывного канала. 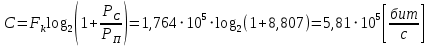 3.7. Демодулятор Когерентный демодулятор производит анализ принятого приёмником колебания z(t) = μsКАМ(t) + n(t), сопоставляя его с известными образцами сигналов, формируемых модулятором. Анализ завершается принятием решения по критерию максимального правдоподобия в пользу наиболее вероятного передаваемого сигнала (символа). Требуется: 1. Изобразить структурную схему когерентного демодулятора, оптимального по критерию максимального правдоподобия для заданного сигнала квадратурной модуляции. (рис. 3.7.1) 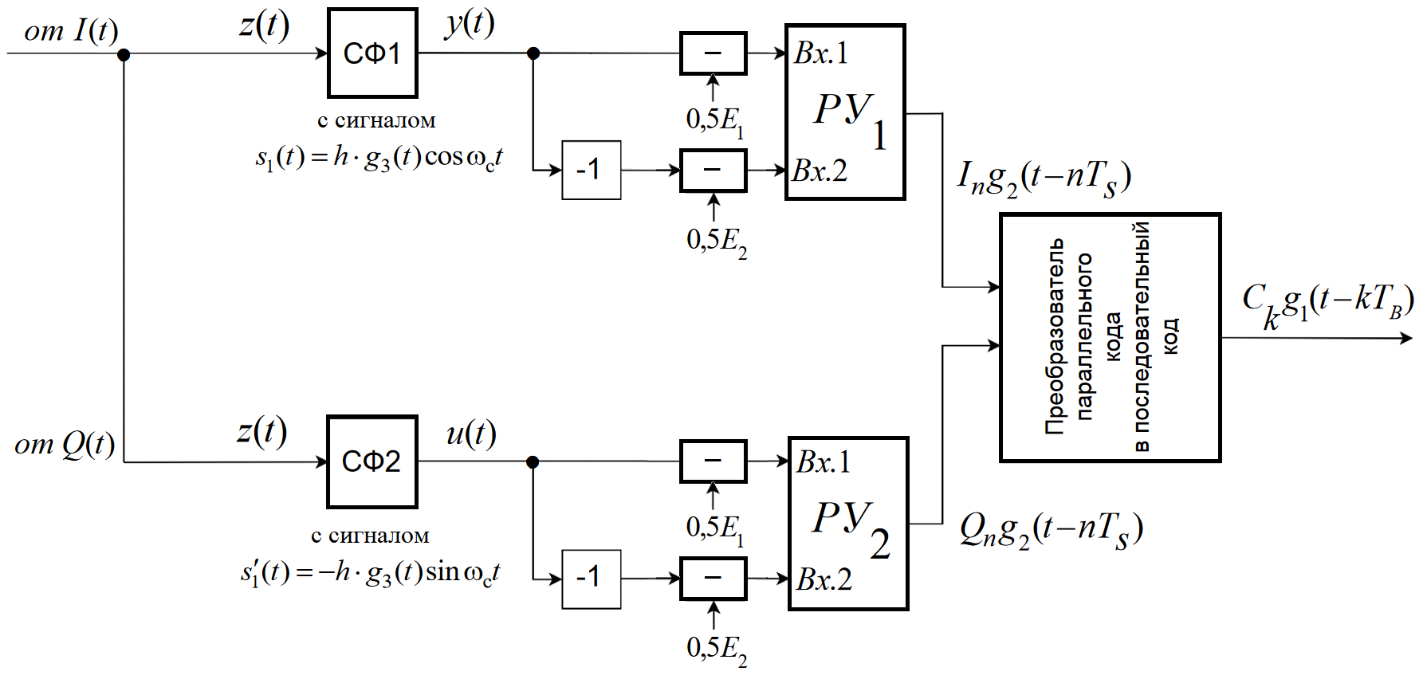 Рисунок 3.7.1 Структурная схема когерентного демодулятора, оптимального по критерию максимального правдоподобия для КФМ-4 2. Написать алгоритмы работы решающих устройств РУ1 и РУ2 в составе когерентного демодулятора. С выхода СФ1 поступает сигнал y(t) = y1(t) + y3(t), где y1(t) – синфазная компонента исходного сигнала, а y3(t) – помеха. Квадратурная компонента y2(t) принимает нулевые значения в моменты времени t = kT. Это свойство является следствием использования квадратурной модуляции. 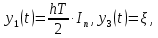 где T = TS, In – численные значения информационных символов. Далее на обоих входах РУ1 из поступившего сигнала вычитается половина энергии ожидаемого. Если в составе сигнала z(t) сигнал помехи n(t) будет равен нулю, то величина ξ также будет равна нулю и на входе, который соответствует пришедшему сигналу, остаётся максимальное напряжение. Например, для информационного символа I0 = h: 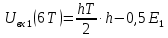 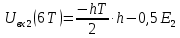 Так как 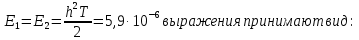 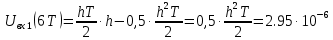 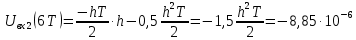 РУ1 принимает решение соответственно входу с максимальным напряжением. Для правильного приёма, РУ1 примет решение о том, что пришёл информационный символ, соответствующий амплитуде h, т.е. «1». 3. Определить вероятности ошибок на выходах РУ1 и РУ2 при значениях символов In и Qn, равных h и – h, когда h = 1 В: 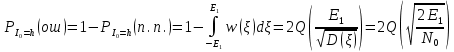 где 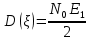 , Q(x) – табулированная функция , Q(x) – табулированная функция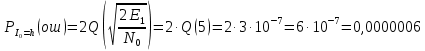 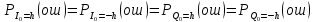 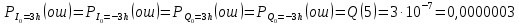 4. Определить вероятности ошибок на выходе преобразователя параллельного кода в последовательный код (ФМС) для заданных параметров сигналов Inи Qn: 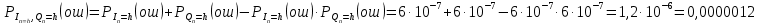 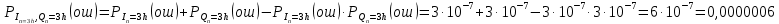 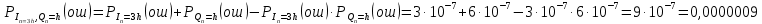 5. Определить среднюю вероятность ошибки на выходе преобразователя: 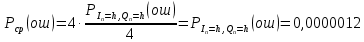 3.8 Декодер 1. Численные значения кодовых символов, которые передавались по каналу связи: 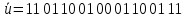 2. Последовательность 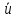 передает сигнал, поступающий на вход демодулятора. После прохождения через демодулятор последовательность передает сигнал, поступающий на вход демодулятора. После прохождения через демодулятор последовательность 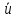 трансформируется в последовательность трансформируется в последовательность 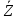 на выходе демодулятора. на выходе демодулятора.В демодуляторе на 7-м тактовом интервале (g = 7) произошла ошибка. Тогда последовательность 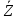 на выходе демодулятора будет равна: на выходе демодулятора будет равна: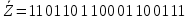 3. Построить решетчатые диаграммы выживших путей декодера для интервалов: t1–t4, t1–t5, t1–t6, t1–t7, t1–t8, t1–t9, t1–t10, t1–t11 (рис. 3.8.2 – 3.8.11). На построенных диаграммах, вычислить метрики путей, входящих в каждый узел диаграммы, выделить фрагменты единственно выживших путей. Рисунок 3.8.1 демонстрирует полную решетчатую диаграмму декодера. 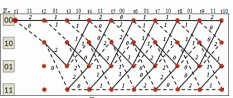 Рисунок 3.8.1. Решетчатая схема декодера Из рисунка 3.8.2 находим пути до точек t4с наименьшей суммой расстояний Хэмминга. 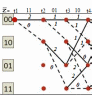 Рисунок 3.8.2. Фрагмент решетчатой диаграммы между моментами t1и t4 Получаем 4 возможных путей. Для удобства назовем узлы латинскими буквами. Что и демонстрируется на рисунке 3.8.3. 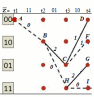 Рисунок 3.8.3. Выжившие пути между моментами t1 иt4 Затем, достраиваем диаграмму до момента t5 (рис. 3.8.4) 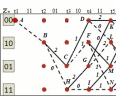 Рисунок 3.8.4. Фрагмент решетчатой диаграммы между моментами t1и t5 Для подсчета минимальной длин пути до узлов K,L,M,N; примем переменную J – за длину пути, таким образом подсчитываем(выделяя полужирным курсивом выжившие пути): 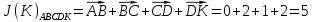 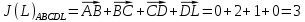 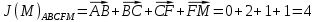 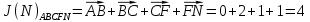 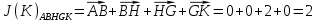 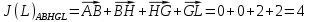 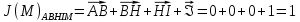 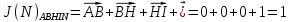 Аналогичным способом считаем пути до узлов X,Y,W,Zна рисунке 3.8.5. 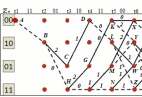 Рисунок 3.8.5. Фрагмент решетчатой диаграммы между моментами t1и t6 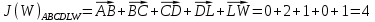 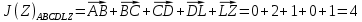 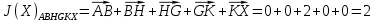 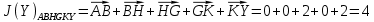 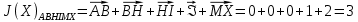 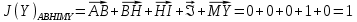 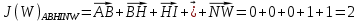 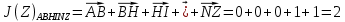 Так как все остальные выжившие пути проходят через точки AиB– эти точки в расчетах учитываться не будут. 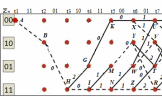 Рисунок 3.8.6. Фрагмент решетчатой диаграммы между моментами t1и t7 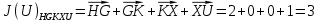 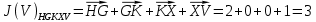 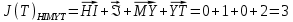 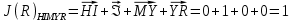 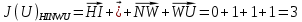 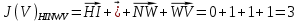 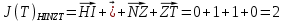 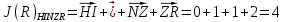 Поскольку в узлы U и Vпришли пути одинаковой длины, произвольно выбираем случайный из них. Например: HGKXU и HGKXV Аналогично предыдущему, по рисунку 3.8.7, находим выжившие пути до момента t8 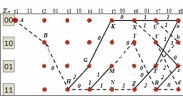 Рисунок 3.8.7. Фрагмент решетчатой диаграммы между моментами t1и t8 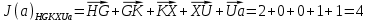 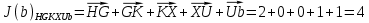 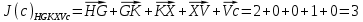 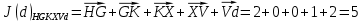 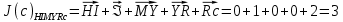 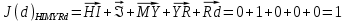 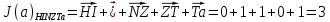 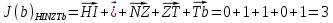 Расчет выживших путей между моментами t1и t9 по рисунку 3.8.8, представлен ниже. 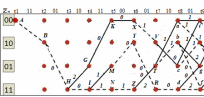 Рисунок 3.8.8. Фрагмент решетчатой диаграммы между моментами t1и t9 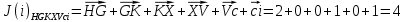 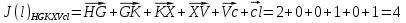 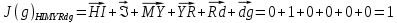 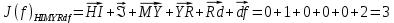 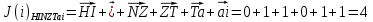 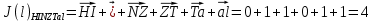 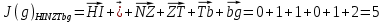 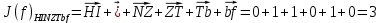 Расчет выживших путей между моментами t1и t10 по рисунку 3.8.9, представлен ниже. 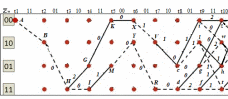 Рисунок 3.8.9. Фрагмент решетчатой диаграммы между моментами t1и t10 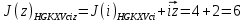 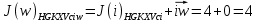 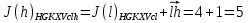 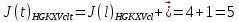 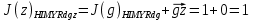 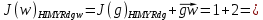 3 3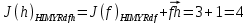 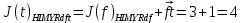 Далее проводится операция отбрасывания: подаются нулевые (не информационные) символы. Таким образом, до следующего момента t11 возможны переходы только в состояния «00», «01»; а до момента t12 – только в состояние «00». (Рис. 3.8.10) 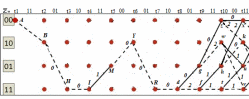 Рисунок 3.8.10. Фрагмент решетчатой диаграммы между моментами t1и t11 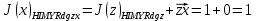 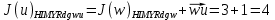 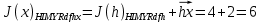 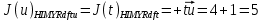 Далее строим на диаграмме найденные пути и достраиваем полученную диаграмму соответствующими рёбрами до момента t12 (рис. 3.8.11) 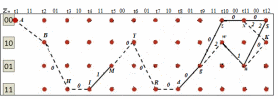 Рисунок 3.8.11. Фрагмент решетчатой диаграммы между моментами t1и t12 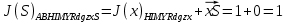 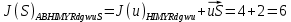 Из чего можно сделать вывод что единственный выживший путь проходит через узлы A, B, H, I, M, Y, R, d, g, z, x, S. Конечный путь изображен на рисунке 3.8.12.  Рисунок 3.8.12. Единственный выживший путь, на выходе декодера Сравнивая пути на решетчатой диаграмме кодера (рис. 3.3.3) и на выходе декодера, можно сделать вывод что они идентичны. Также при наложении выжившего пути на решётчатую диаграмму кодера (рисунок 3.3.3), получим информационный символы равные информационным символам на выходе кодера. Следовательно, можно считать что, ошибка на выходе демодулятора была исправлена Таблица, итоговых значений входных сигналов на каждом этапе схемы ЦС, представлена ниже
ЛИТЕРАТУРА Сальников А.П. Теория электрической связи: Конспект лекций / СПбГУТ. – СПб., 2007. – 273 с.: ил. Общая теория связи: методические указания к выполнению курсовой работы / Л. Н. Куликов, М. Н. Москалец, М. Н. Чесноков. – СПб. : Издательство СПбГУТ, 2012. – 80 с. Санкт-Петербург 2022 |
