КУРСАЧ СОСЕДА. Расчёт основных характеристик цифровой системы связи с использованием квадратурной модуляции
 Скачать 2.37 Mb. Скачать 2.37 Mb.
|
|
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч-Бруевича» __________________________________________________________ Факультет фундаментальной подготовки Кафедра теоретических основ телекоммуникаций КУРСОВАЯ РАБОТА учебная дисциплина «Теория информации» Тема: «Расчёт основных характеристик цифровой системы связи с использованием квадратурной модуляции» Выполнил студент II курса группы ИБС-03 Шахов С.К., номер зачётной книжки № 2005478; номер выполненного варианта 18; Проверил Оценка __________(подпись) Цель курсовой работы (КР) – изучить принципы работы системы цифровой передачи аналоговых сообщений и рассчитать основные характеристики входящих в неё функциональных узлов. 1. Структурная схема системы цифровой связи Система связи предназначена для передачи аналоговых сообщений по цифровому каналу связи. Структурная схема дляКАМ-16 и КФМ-4 представлена на рис. 1.1.  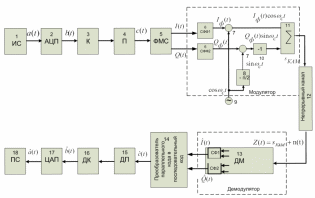 Рис. 1.1. Структурная схема системы цифровой связи. Входящие в систему цифровой связи функциональные узлы имеют следующие назначения: источник сообщений (ИС) создаёт реализацииa(t) случайного процесса A(t); аналого-цифровой преобразователь (АЦП) преобразует аналоговый сигнал от источника сообщения в последовательность его двоичных цифровых отсчётов; кодер (К) включает в цифровой поток от АЦП дополнительные символы, предназначенные для повышения помехоустойчивости системы связи; формирователь модулирующих сигналов (ФМС) служит для получения модулирующих сигналов I(t) и Q(t), соответствующих заданному виду модуляции; перемножители (ПМ1, ПМ2) модулятора – для получения БМ сигналов: синфазного I(t)cosωСtи квадратурного Q(t)sinωСt. Фазовращатель на угол 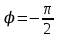 модулятора – для получения второго несущего колебания, ортогонального по отношению к первому; модулятора – для получения второго несущего колебания, ортогонального по отношению к первому; генератор гармонических 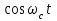 колебаний – для получения несущего колебания; колебаний – для получения несущего колебания; сумматор модулятора – для объединения синфазного и квадратурного сигналов в единый сигнал с квадратурной модуляцией SКАМ(t) = I(t)cosωСt + Q(t)sinωСt; непрерывный канал – среда распространения сигнала SКАМ(t); демодулятор – для анализа приходящего сигнала, искажённого помехами, и принятия решения о переданном сообщении; преобразователь параллельного кода в последовательный код – для преобразования сигнала с выхода демодулятора в последовательный формат кодовых комбинаций; Декодер (ДК) – для исправления части ошибок, возникших при приёме сообщений вследствие влияния помех; цифро-аналоговый преобразователь (ЦАП) – для восстановления аналоговой формы сигнала по принятым его цифровым отсчетам; получатель сообщений (ПС). 2. Исходные данные для расчета системы цифровой связи Исходные данные (по варианту 18) указаны в табл. 1 Таблица 1
3. Расчет системы цифровой связи 3.1. Источник сообщения Источник сообщения (ИС) вырабатывает реализации 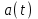 стационарного случайного процесса стационарного случайного процесса 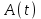 типа квазибелого шума с параметрами типа квазибелого шума с параметрами 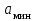 , ,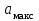 и и 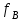 . Мгновенные значения сообщения равновероятны в интервале от значения . Мгновенные значения сообщения равновероятны в интервале от значения 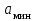 до значения до значения 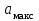 . .Требуется: Написать аналитические выражения для плотности вероятности w(a) мгновенных значений сообщения, функции распределения 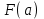 и построить их графики. и построить их графики. Плотность вероятности мгновенных сообщений (рис. 3.1.1.1): 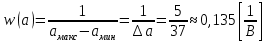 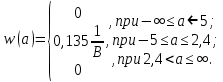    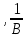 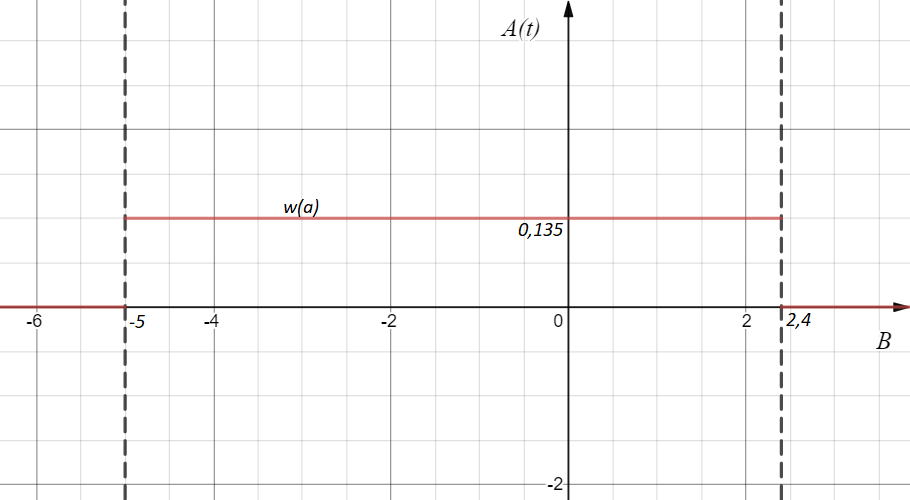 Рисунок 3.1.1.1 График распределения и плотности вероятности A(t) для w(a)  Функция распределения мгновенных значений сообщения (рис. 3.1.1.2): Функция распределения мгновенных значений сообщения (рис. 3.1.1.2):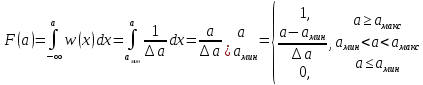 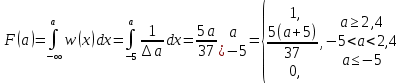   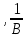 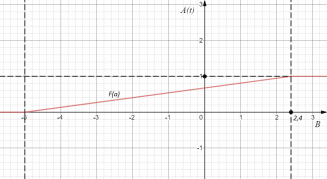 Рисунок 3.1.1.2 График распределения и плотности вероятности A(t) для F(a) Рассчитать математическое ожидание M[A(t)] и дисперсию D[A(t)] сообщения A(t).   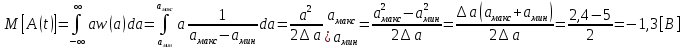 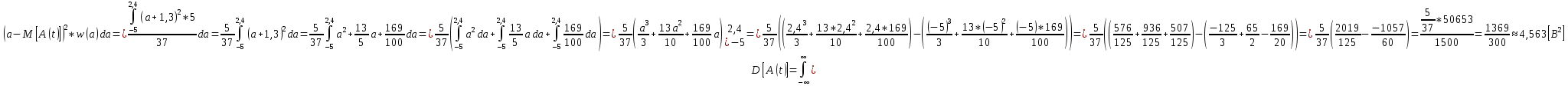 Написать аналитическое выражение для спектральной плотности мощности 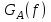 сообщения сообщения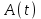 и построить график. и построить график. 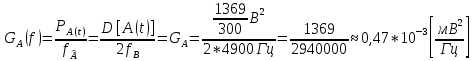 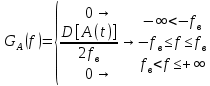 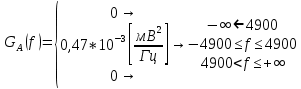 GA(f) на интервале от –fв до fв обозначим через G0 , одностороння спектральная плотность G0(f)=2GA(f) на частотном интервале 0 ≤ f ≤ fв и равна 0 на интервале fв <f ≤ ∞. 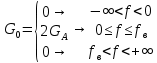 Графики GA(f) и 2G0(f) приведены на рисунке 3.1.3. 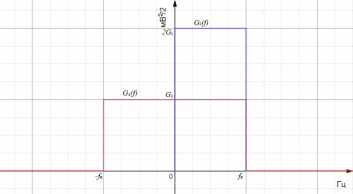 Рисунок 3.1.3 График аналитического выражение для спектральной плотности мощности и односторонней спектральной плотности сообщения А(t) 4. Найти аналитическое выражение для корреляционной функции 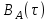 сообщения сообщения 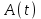 и построить график. По форме графика и построить график. По форме графика 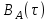 определить, является ли сообщение определить, является ли сообщение 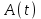 эргодическим случайным процессом или не является таковым. Корреляционную функцию случайного процесса можно определить через его энергетический спектр по теореме Винера-Хинчина [1, стр.117 – 119]. эргодическим случайным процессом или не является таковым. Корреляционную функцию случайного процесса можно определить через его энергетический спектр по теореме Винера-Хинчина [1, стр.117 – 119].В соответствии с теоремой Винера-Хинчина корреляционная функция BA(τ)стационарного случайного процесса A(t)определяется по формуле:  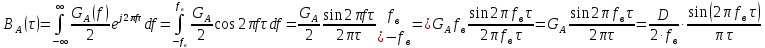 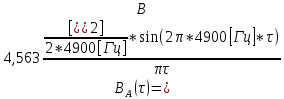 График корреляционной функции 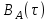 сообщения A(t) изображен на рисунке 3.1.4. сообщения A(t) изображен на рисунке 3.1.4.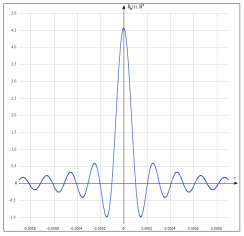 Рисунок 3.1.4. График корреляционной функции сообщения Так как выполняется необходимое и достаточное условие 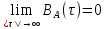 , то сообщение A(t) можно считать эргодическим случайным процессом. , то сообщение A(t) можно считать эргодическим случайным процессом.3.2. Аналого-цифровой преобразователь Аналого-цифровой преобразователь (АЦП) преобразует реализации аналогового (непрерывного) сообщения 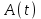 в цифровую форму– поток двоичных символов нулей и единиц, т. е. в последовательность прямоугольных импульсов, где «0» имеет нулевое напряжение, а «1» прямоугольный импульс положительной полярности. Амплитуда импульсов в цифровую форму– поток двоичных символов нулей и единиц, т. е. в последовательность прямоугольных импульсов, где «0» имеет нулевое напряжение, а «1» прямоугольный импульс положительной полярности. Амплитуда импульсов 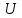 равна равна 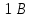 . .Преобразование аналогового сигнала в цифровую форму осуществляется в три этапа. На первом этапе производится дискретизация реализации 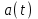 сообщения сообщения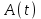 по времени. В моменты времени по времени. В моменты времени 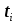 берутся непрерывные по уровню отсчёты берутся непрерывные по уровню отсчёты 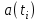 мгновенных значений реализации мгновенных значений реализации 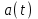 . Расстояние между отсчётами равно интервалу . Расстояние между отсчётами равно интервалу 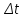 , величина которого определяется в соответствии с теоремой Котельникова. , величина которого определяется в соответствии с теоремой Котельникова. На втором этапе выполняется квантование точных отсчётов 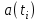 по уровню. Для этого интервал по уровню. Для этого интервал 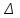 a равный разности ∆a= a равный разности ∆a=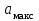 - -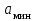 разбивается на уровни квантования с постоянным шагом ∆=14,8 мВ. Уровни квантования нумеруются целыми числами разбивается на уровни квантования с постоянным шагом ∆=14,8 мВ. Уровни квантования нумеруются целыми числами 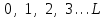 . Нумерация уровней начинается с уровня, которому соответствует значение . Нумерация уровней начинается с уровня, которому соответствует значение 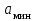 , и заканчивается на уровне, которому соответствует значение , и заканчивается на уровне, которому соответствует значение 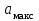 . Обычно величина шага квантования ∆ выбирается так, чтобы число уровней квантования . Обычно величина шага квантования ∆ выбирается так, чтобы число уровней квантования 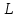 можно представить в виде можно представить в виде 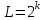 , где , где 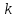 целое число. целое число. Каждый аналоговый отсчёт 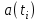 заменяется значением ближайшего к нему уровня квантования заменяется значением ближайшего к нему уровня квантования 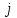 в виде целого числа, удовлетворяющего неравенству в виде целого числа, удовлетворяющего неравенству 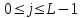 . Получаем квантованный отсчёт . Получаем квантованный отсчёт 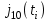 в виде целого числа в десятичной форме счисления. в виде целого числа в десятичной форме счисления. На третьем этапе число 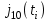 в десятичной форме переводится в двоичную форму счисления в десятичной форме переводится в двоичную форму счисления 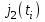 в виде последовательности в виде последовательности 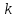 двоичных символов и на выходе АЦП появляется сигнал в виде двоичной цифровой последовательности двоичных символов и на выходе АЦП появляется сигнал в виде двоичной цифровой последовательности 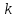 информационных символов. информационных символов. Требуется: 1. Рассчитать интервал дискретизации ∆t для получения отсчётов 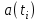 реализации реализации 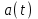 , , 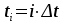 , , 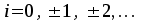 Согласно с теоремой Котельникова 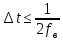 , тогда максимальный шаг дискретизации , тогда максимальный шаг дискретизации 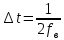 . .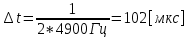 2. Рассчитать частоту дискретизации Fд. 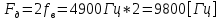 3. Определить число уровней квантования L. 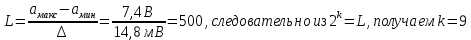 4. Рассчитать мощность шума квантования 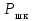 и сравнить ее с мощностью непрерывного сообщения и сравнить ее с мощностью непрерывного сообщения 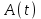 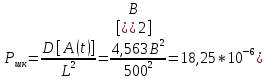 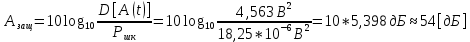 5. Записать k разрядное двоичное число, соответствующее заданному уровню квантования j. 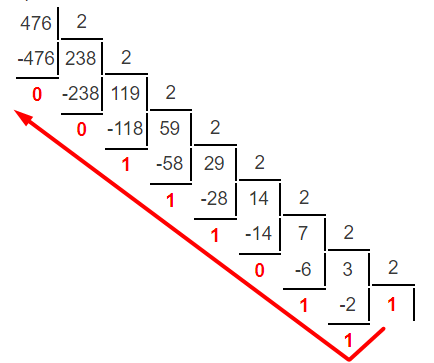 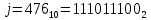 6. Начертить временную диаграмму отклика АЦП 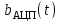 на заданный уровень квантования на заданный уровень квантования 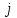 в виде последовательности импульсов, сопоставляя единичным символам прямоугольные импульсы положительной полярности, а нулевым – нулевые напряжения. Над импульсами надписать значения соответствующих двоичных информационных символов (рис.3.2.1). Длительность отклика АЦП на каждый отсчёт не должна превышать интервала дискретизации в виде последовательности импульсов, сопоставляя единичным символам прямоугольные импульсы положительной полярности, а нулевым – нулевые напряжения. Над импульсами надписать значения соответствующих двоичных информационных символов (рис.3.2.1). Длительность отклика АЦП на каждый отсчёт не должна превышать интервала дискретизации 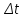 . .           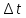 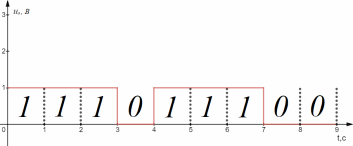 Рисунок 3.2.1. Осциллограмма сигнала на выходе АЦП | |||||||||||||||||||||||
