Курсовая работа по дисциплине ТЭС. Курсовая ТЭС. Расчёт основных характеристик цифровой системы связи с использованием квадратурной модуляции
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
Формирователь модулирующих символовТребуется: 1) Изобразить сигнальное созвездие для заданного вида модуляции; 2) Изобразить график реализации 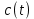 случайного процесса случайного процесса 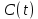 , формируемого с выхода блока сверточного кодера (К). Реализация , формируемого с выхода блока сверточного кодера (К). Реализация 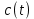 поступает на вход блока ФМС на первых 16 бинарных интервалах длительностью поступает на вход блока ФМС на первых 16 бинарных интервалах длительностью 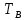 . Написать аналитическое выражение для случайного процесса . Написать аналитическое выражение для случайного процесса 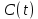 ; ;3) В соответствии с сигнальным созвездием модулятора КАМ-16 или КФМ-4 изобразить графики реализаций 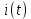 и и 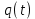 на выходе блока ФМС, соответствующие входной реализации на выходе блока ФМС, соответствующие входной реализации 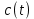 . Написать аналитические выражения для случайных процессов . Написать аналитические выражения для случайных процессов 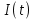 и и 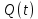 ; ; 4) Написать аналитические выражения для корреляционной функции 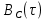 и спектральной плотности мощности и спектральной плотности мощности 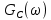 входного случайного процесса входного случайного процесса 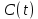 и построить графики этих функций; и построить графики этих функций; 5) Написать аналитические выражения для корреляционных функций 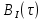 и и 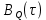 , спектральных плотностей мощности , спектральных плотностей мощности 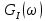 и и  случайных процессов случайных процессов 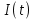 и и 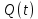 . Построить графики этих функций; . Построить графики этих функций; 6) Сравнить графики корреляционных функций и спектральных плотностей мощности сигналов на входе и выходе блока ФМС. Привести краткое описание результатов сравнения и, используя общие положения теории преобразования Фурье, пояснить, почему спектр выходных сигналов уже спектра входного сигнала. 1) Сигнальное созвездие КАМ-16 представлено на рис.9. 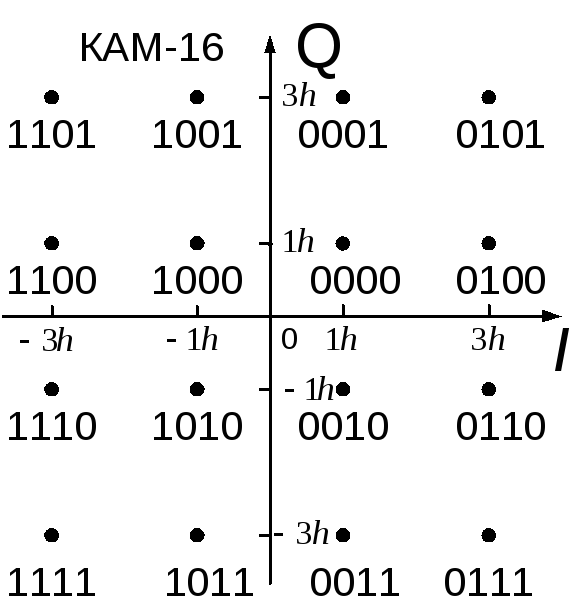 Рис.10 Сигнальное созвездие КАМ-16 2) С выхода кодера на формирователь модулирующих импульсов (ФМС) поступает последовательность из 16 однополярных импульсов амплитудой в 1 В и длительностью 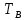 , временная диаграмма которых представлена на рис.11. , временная диаграмма которых представлена на рис.11.   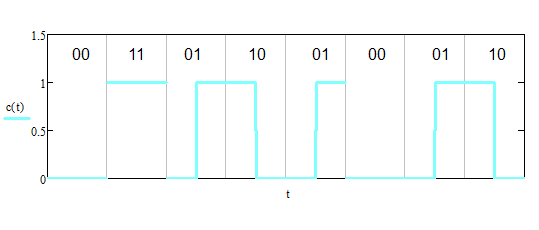 Рис.11 Временная диаграмма реализации c(t) случайного процесса C(t), формируемого с выхода блока свёрточного кодера Аналитическое выражение для случайного процесса 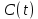 можно записать в виде: можно записать в виде: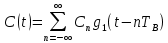 (19) (19)где: 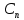 – случайная величина, заданная на бинарном интервале n, которая принимает одно из двух значений 1 или 0 c вероятностью 0.5 каждое; – случайная величина, заданная на бинарном интервале n, которая принимает одно из двух значений 1 или 0 c вероятностью 0.5 каждое;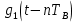 - прямоугольный импульс такой же формы, как и импульс - прямоугольный импульс такой же формы, как и импульс 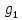 , но сдвинутый вправо на время , но сдвинутый вправо на время 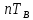 ( (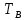 - бинарный интервал); - бинарный интервал);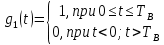 (20) (20)3) В соответствии с сигнальным созвездием КАМ-16 и реализацией 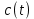 на выходе ФМС формируются две реализации: на выходе ФМС формируются две реализации: 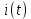 и и 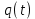 . Графики (рис. 12) иллюстрируют пример, когда по заданной реализации . Графики (рис. 12) иллюстрируют пример, когда по заданной реализации 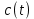 входного случайного процесса входного случайного процесса 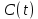 с использованием сигнального созвездия КАМ-16 строятся реализации с использованием сигнального созвездия КАМ-16 строятся реализации 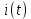 и и 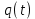 выходных случайных процессов выходных случайных процессов 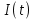 и и 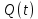 . .     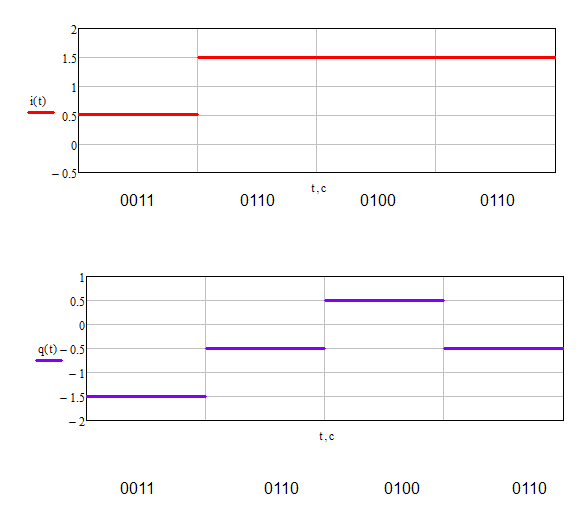 Рис. 12 Временные диаграммы реализаций i(t) и q(t), формируемых на выходе ФМС Аналитические выражения для случайных процессов 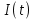 и и 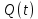 можно записать в виде: можно записать в виде: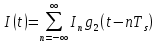 (21) (21)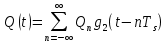 (22) (22)где: 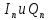 – случайные величины, заданные на символьном интервале n, которые принимают одно из четырёх значений – случайные величины, заданные на символьном интервале n, которые принимают одно из четырёх значений 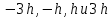 c вероятностью 0.25 каждое согласно сигнальному созвездию КАМ-16; c вероятностью 0.25 каждое согласно сигнальному созвездию КАМ-16; - прямоугольный импульс такой же формы, как и импульс - прямоугольный импульс такой же формы, как и импульс 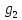 , но сдвинутый вправо на время , но сдвинутый вправо на время 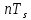 ( (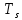 - символьный интервал); - символьный интервал);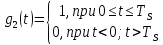 (23) (23)Поскольку сообщение сигнал  представляет собой случайный синхронный телеграфный сигнал, то аналитическое выражение корреляционной функции представляет собой случайный синхронный телеграфный сигнал, то аналитическое выражение корреляционной функции  можно представить следующим образом: можно представить следующим образом: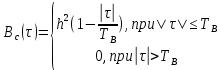 (24) (24)На основании теоремы Винера-Хинчина запишем аналитическое выражение для спектральной плотности мощности сигнала 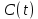 : :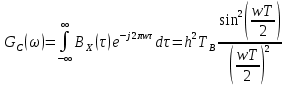 (25) (25)На рис.13 и рис.14 изображены графики для аналитических выражений (24) и (25). 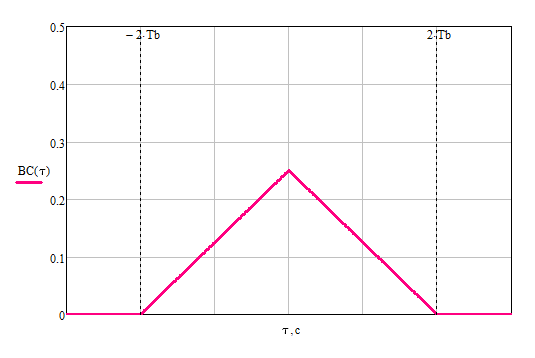 Рис. 13 График корреляционной функции 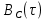 сигнала C(t) сигнала C(t)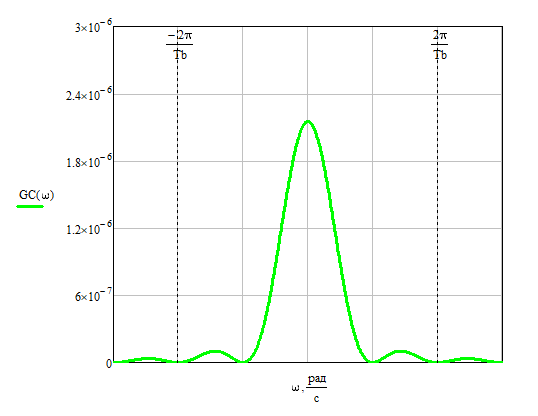 Рис. 14 График функции спектральной плотности мощности 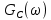 сигнала C(t) сигнала C(t)Корреляционные функции 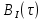 и и 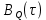 случайных процессов случайных процессов 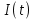 и и 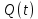 на выходе блока ФМС определяются по аналогичной методике определения корреляционной функции случайного процесса на выходе блока ФМС определяются по аналогичной методике определения корреляционной функции случайного процесса 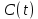 , поступающего на вход блока ФМС. Поскольку процесс , поступающего на вход блока ФМС. Поскольку процесс 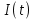 имеет те же вероятностные характеристики, что и имеет те же вероятностные характеристики, что и 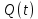 , то: , то: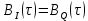 (27) (27)Аналитические выражения для этих функций имеют вид: 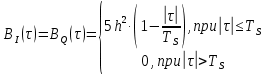 (28) (28)Тогда, используя теорему Винера-Хинчина, можно получить аналитические выражения спектральных плотностей мощностей 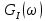 и и 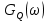 . Они так же будут равны друг другу. Получаем: . Они так же будут равны друг другу. Получаем: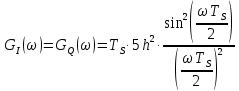 (29) (29)Графики для этих аналитических выражений изображены на рис.15, рис.16, рис.17 и рис.18 соответственно. 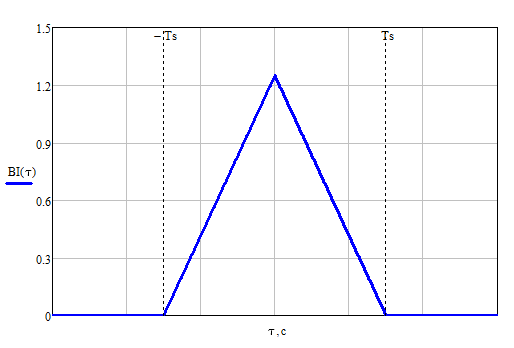 Рис.15 График корреляционной функции 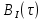 сигнала сигнала 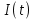 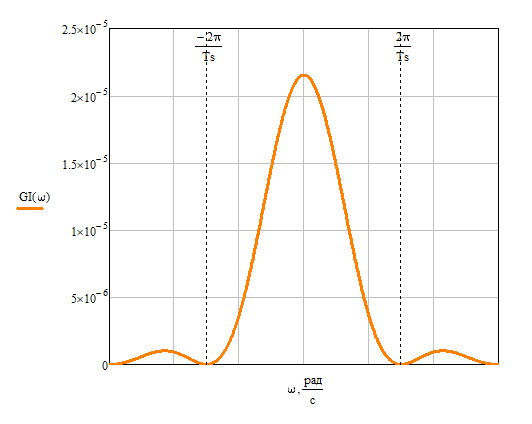 Рис. 16 График функции спектральной плотности мощности  сигнала сигнала 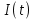 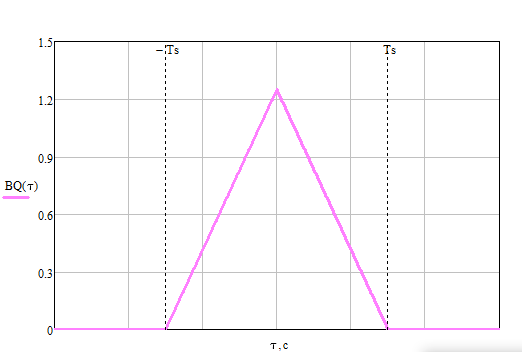 Рис. 17 График корреляционной функции 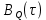 сигнала сигнала 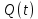 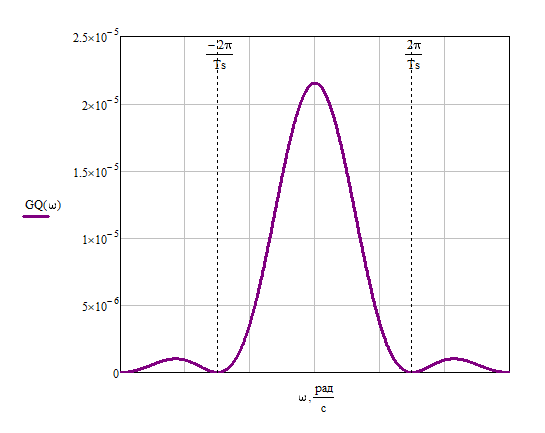 Рис. 18 График функции спектральной плотности мощности  сигнала сигнала 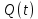 6) Сравнение корреляционных функций и спектральных мощностей представлены на рис.19 и рис.20. 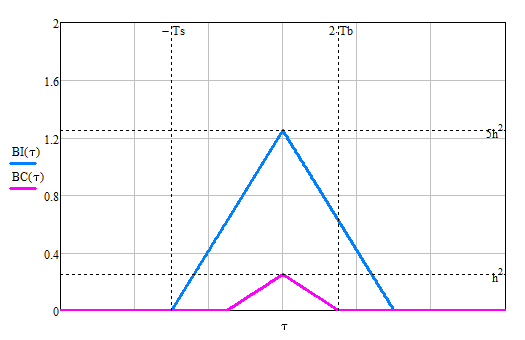 Рис. 19 Сравнение корреляционных функций 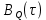 и и 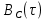 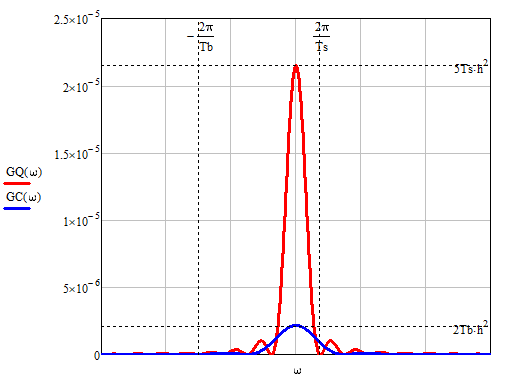 Рис. 20 Сравнение спектральных плотностей мощности  и и 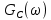 На графиках видно, что спектр выходных сигналов значительно уже спектра входного сигнала. Это объясняется теоремой подобия преобразования Фурье. Спектр выходных сигналов в 2 раза уже спектра входного сигнала, а спектральные плотности мощностей в 4 раза уже спектральной плотности мощности входного сигнала. Графики корреляционных функций отличаются друг от друга в 4 раза, как и спектральные плотности, что объясняется теоремой Винера-Хинчина. |
